AP Chemistry - Chapter 4 (copy)

Note To Self: [THIS CHAPTER IS MAINLY MATH BASED] Look Back On PS 4-1, 4-2, 4-3, Ch 4 Practice Test, and Ch 4 ASP Pt 1 + 2

(4.4) Gravimetric Analysis

a method in chemical analysis in which the desired substance is converted to a substance of known composition that can be separated from the sample and weighed

(4.4) Combustion Analysis

determining the formula of the hydrocarbon by combustion

combustion involves the addition oxygen to another element

hydrocarbon always produced CO₂ and H₂O when burned completely

(4.4) SOLVE: An oxygenated hydrocarbon containing only C, H, and O is analyzed. After the complete combustion of 10.68 mg of the compound, the subsequent capture of the products in absorbers yielded 16.01 mg of CO2 and 4.37 mg H2O. The molar mass of the compound is 176.1 g/mol. What are the empirical and molecular formulas of the compound?

10.68mg / 1000 = 0.01068g

16.01mg / 1000 = 0.01601

4.37 mg / 1000 = 4.37x10^-3

mass of C: 0.01601g CO2 x (12.01g C / 44.01g CO2) = 4.369x10^-3g C

mass of H: 4.37x10^-3g H2O x (2.02g H / 18.02g H2O) = 4.90x10^-4g H

mass of O: 0.01068g - (4.369x10^-3g + 4.90x10^-4g) = 5.82x10^-3g O

mol C: 4.369x10^-3g C x (1 mol C / 12.01g C) = 3.638x10^-4 mol C

mol H: 4.90x10^-4g H x (1 mol H / 1.01g H) = 4.85x10^-4 mol H

mol O: 5.82x10^-3g O x (1 mol O / 16.00g O) = 3.6375x10^-4 mol O

C: 3.638x10^-4 mol / 3.6375x10^-4 mol = 1 x 3 = 3

H: 4.85x10^-4 mol / 3.6375x10^-4 mol = 1.33 x 3 = 4

O: 3.6375x10^-4 mol / 3.6375x10^-4 mol = 1 x 3 = 3

Empirical Formula: C3H4O3

Empirical Formula Molar Mass: 3(12.01g) + 4(1.01g) + 3(16.00g) = 88.07g

176.1g / 88.07g = 2 -> 2(C3H4O3) = C6H8O6

Molecular Formula: C6H8O6

(4.5) Molarity Formula

Molarity = moles / Liters

(4.5) Dilution of Stock Solutions Formula

M₁V₁ = M₂V₂

(4.5) Why is molarity based on volume of solution rather than volume of solvent?

Molarity is based on volume of solution instead of the volume of solvent because if one liter of water is added to one mole of a solid compound, the final volume will not be one liter, and the final concentration will not be exactly one mole/L.

(4.5) What should be noted about [Cl^-] vs. [CuCl₂] when CuCl₂ is completely dissolved in water?

The molarity of [Cl^-] will double the molarity of [Cu²⁺] because there are two moles of [Cl^-] ions for each mole of CuCl₂ while there is only one mole of [Cu²⁺] for each mole of CuCl₂.

(4.5) Describe how to make 0.5 liters of a 0.0200 M KMnO4 solution (in a 500 mL volumetric flask) using solid KMnO4. You will need to calculate the mass of solid KMnO4 to be used.

Molarity = moles/volume -> moles = Molarity x volume = 0.0200M KMnO4 x 0.5 = 0.01 mol KMnO4

Molar Mass of KMnO4: 39.10g + 54.94g + 4(16.00g) = 158.04g

0.01 mol KMnO4 x (158.04g KMnO4 / 1 mol KMnO4) = 1.58g KMnO4

In order to make 0.5 liters of a 0.0200M KMnO4 solution you must get 1.58g of KMnO4 and place it in a 0.5L flask. Then you need to fill the flask up with distilled water until it reaches the 0.5L mark on the flask.

(4.5) Describe how to make 1 liter of a 0.00200 M Kr2Cr2O7 solution (in a 1 L volumetric flask) using a 0.100 M stock Kr2Cr2O7 solution. You will need to calculate the amount of stock solution needed using M1V1=M2V2.

M1V1 = M2V2 -> 1L(0.00200M) = V2(0.100M) -> V2 = 1L(0.00200M)/0.100M = 0.0200L

To make 1L of 0.00200M Kr2Cr2O7 solution, you must get 0.0200L of a 0.100M Kr2Cr2O7 solution and place it in a 1L flask. You then fill the flask up with distilled water until it reaches the 1L mark on the flask.

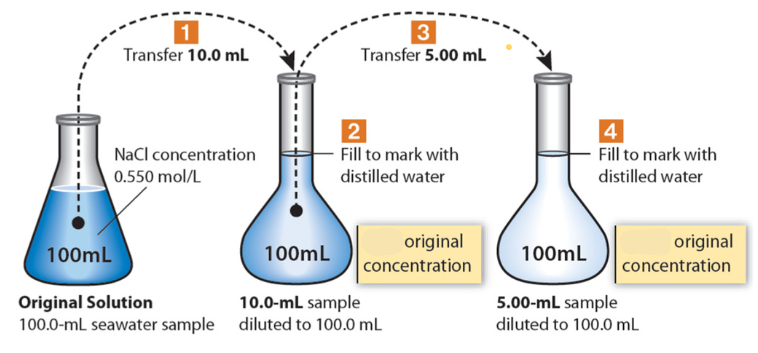
(4.5) Serial Dilutions

1/10 original concentration

1/200 original concentration

(4.5) What would the final amount relative to the original concentration be in a serial dilution if 10.0 mL of the original solution was transferred and diluted in a 100 mL flask, then 1.0 mL of the new solution was transferred and diluted in another 100 mL flask? (State answer as a fraction of the original.)

The final amount relative to the original concentration is 1/1000.

(4.6) pH and pOH Formulas

pH = -log[H₃O⁺] or [H⁺] ; [H₃O⁺] or [H⁺] = 10^-pH

pH = -log[OH^-] ; [OH^-] = 10^-pOH

pH + pOH = 14

(4.6) How are significant figures handled in pH/concentration calculations?

The amount of decimal places the pH will have is determined by the amount of significant figures in the concentration. For example, if the concentration has two significant figures, the pH will go to two decimal places. The vice versa of this applies also.

(4.6) What is the pH of a 0.250 M HClO₄ solution?

pH = -log[H₃O⁺] = -log[0.250] = 0.602

(4.8) What are Acid-Base Reactions are also called? Why?

They are also called neutralization reaction because the acid neutralizes the base (or vice versa)

(4.8) What are titrations used to determine?

Concentrations of unknown substances

(4.8) Titrant vs Analyte

Titrant: solution of known concentration

Analyte: solution of unknown concentration

(4.8) In a titration, what do you have to know about the titrant (known) in order to determine the concentration or mass of the analyte (unknown)?

You need to know the concentration of the titrant and the volume that had been added at exactly the point of complete reaction.

(4.8) In a titration, what is the equivalence point?

It is when the amount of OH^- added exactly equals the amount of H₃O⁺ that can be supplied by the acid.

or

when enough titrant has been added to neutralize the unknown

(4.8) What are indicators often used for in titrations?

Used to signal ROUGHLY when equivalence is reached

(3.8) When is equivalence reached?

When acid and base completely neutralize each other.

(3.8) When is the endpoint reached?

When the indicator changes color.

(if a proper indicator is used, the endpoint is near the equivalence point)

(3.8) What does standardization mean with respect to titrations?

This means that the concentration of an analytical reagent is determined accurately.

(3.8) Titration Formula

# of H⁺ x M_a x V_a = # of OH^- x M_b x V_b

(3.8) A 50.00 mL sample of aqueous Ca(OH)₂ requires 34.66 mL of 0.0980 M nitric acid for neutralization. What is [Ca(OH)₂]?

0.0340M Ca(OH)₂

(3.8) 75 mL of 0.25M HCl is mixed with 225 mL of 0.055M Ba(OH)₂. What is the concentration of the excess H⁺ or OH^-?

0.020M OH

(4.9) Spectrophotometry

interaction between light and matter that provides quantitative information about solution concentration

(4.9) What does the amount of light absorbed by a sample depends on?

Path length and solute concentration

(4.9) Beer’s Law

A = εbc

A = absorbance (NO units)

ε = molar absorptivity (M^-1 cm^-1)

b = path length (cm)

c = concentration (M)

Beer’s Law Equation reflects…

y = mx

y = absorbance(A)

x = concentration(c)

m = molar absorptivity(ε) x path length(b)

(4.9) What is the relationship between absorbance and concentration?

The relationship is linear.

(This means that molar absorptivity and path length is CONSTANT)

(4.9) Transmittance vs Absorbance

Transmittance: the amount of light allowed through the solution

Absorbance: amount of light absorbed

(4.9) Transmittance Formula

T = I / I₀ or T(%) = 100(I / I₀)

T = Transmittance

I = intensity of light after passing through the sample

I₀ = intensity of light before passing through the sample

(4.9) Relationship between absorbance and transmittance Formulas

T = 10^-A

A = -log T

%T = 100T

(4.9) Steps to Measuring Transmittance and Absorbance

1) Spectrophtotometer or colorimeter is calibrated by using a cuvette (special test tube used in spectrophotometers) containing distilled water that is used to “train“ the device to read as 100% T (or 0 Abs).

2) Set the proper wavelength so that the color of light observed from a solution is the light that is allowed to pass through after other colors have been absorbed. The best wavelength to pick is the complementary color of the solution.

3) Once the device is calibrated, the cuvette can be filled with solutions of known concentrations to establish a calibration plot. This plot can be used to find an unknown concentration of a solution from a measured Absorbance.