MM - Chapter 6: Lossless Compression Algorithms (copy)

3 main steps of a compression scheme

Three main steps in a compression scheme

• Transform: the input data is transformed to a new representation that is easier or more efficient to compress.

• Quantization: we use a limited number of reconstruction levels (fewer than in the original signal) ➔ we may introduce loss of information

• Entropy Coding: we assign a codewords to each output level or symbol (forming a binary bitstream)

lossy vs lossless (kort)

If the compression and decompression processes induce no information loss, then the compression scheme is lossless; otherwise, it is lossy.

vb lossless: morse code

wat is entropy

Entropie η

• Definitie:
  Entropie η is de gewogen som van de zelf-informatie van de symbolen
  → log₂(1 / pᵢ), waarbij pᵢ de kans is op symbool i

• Betekenis:
  → η geeft de gemiddelde hoeveelheid informatie weer die per symbool in bron S zit

Belang

• Entropie η bepaalt de ondergrens voor het gemiddelde aantal bits dat je nodig hebt om elk symbool in S te coderen:

  

  waarbij l̄ = gemiddelde lengte (in bits) van de codewoorden die de encoder produceert

Uitleg

• Hoe lager de entropie, hoe voorspelbaarder de bron (minder bits nodig)

• Hoe hoger de entropie, hoe onvoorspelbaarder (meer bits nodig)

• Informatiecodering kan dus nooit gemiddeld minder bits gebruiken dan de entropie

---

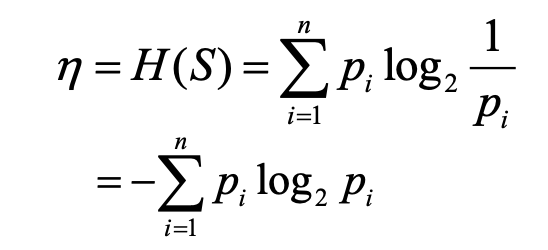
Voorbeeld

Stel: bron S met symbolen A, B, C, D

• p(A) = 0.5 → log₂(1/0.5) = 1 bit

• p(B) = 0.25 → log₂(1/0.25) = 2 bits

• p(C) = 0.125 → log₂(1/0.125) = 3 bits

• p(D) = 0.125 → log₂(1/0.125) = 3 bits

Gemiddelde entropie η:
η = 0.5×1 + 0.25×2 + 0.125×3 + 0.125×3 = 1.75 bits/symbool

→ elke codering moet dus gemiddeld minstens 1.75 bits per symbool gebruiken

run length coding

Memoryless Source (geheugenloze bron)

• Definitie:
  Informatiebron waarbij elk symbool onafhankelijk is van de vorige symbolen
  → de waarde van het huidige symbool hangt niet af van eerder verschenen symbolen

Run-Length Coding (RLC)

• Wat doet RLC?
  In plaats van aan te nemen dat de bron geheugenloos is, maakt RLC gebruik van geheugen dat in de bron aanwezig is

• Idee erachter:
  Als een informatiebron de eigenschap heeft dat symbolen vaak in opeenvolgende groepen verschijnen (bijvoorbeeld meerdere keren hetzelfde symbool na elkaar), kan je die groep efficiënt coderen:
  → je codeert het symbool én de lengte van de reeks (run)

Waarom werkt dit goed?

• Voorbeeldsituatie:
  In plaats van “A A A A A” apart te coderen als vijf keer A, schrijf je gewoon “A, 5” (symbool + lengte)
  → veel efficiënter als er veel herhaling is

shannon-fano algorithm - variable length coding (VLC)

Shannon-Fano codering (VLC)

● Sorteer symbolen op frequentie
● Splits recursief in 2 groepen met gelijke tellingen

• 0 → links

• 1 → rechts

Herhaal tot 1 symbool per groep
● Resultaat = boom → codewoorden

Voorbeeld HELLO

Symbool	Telling
L	2
H	1
E	1
O	1

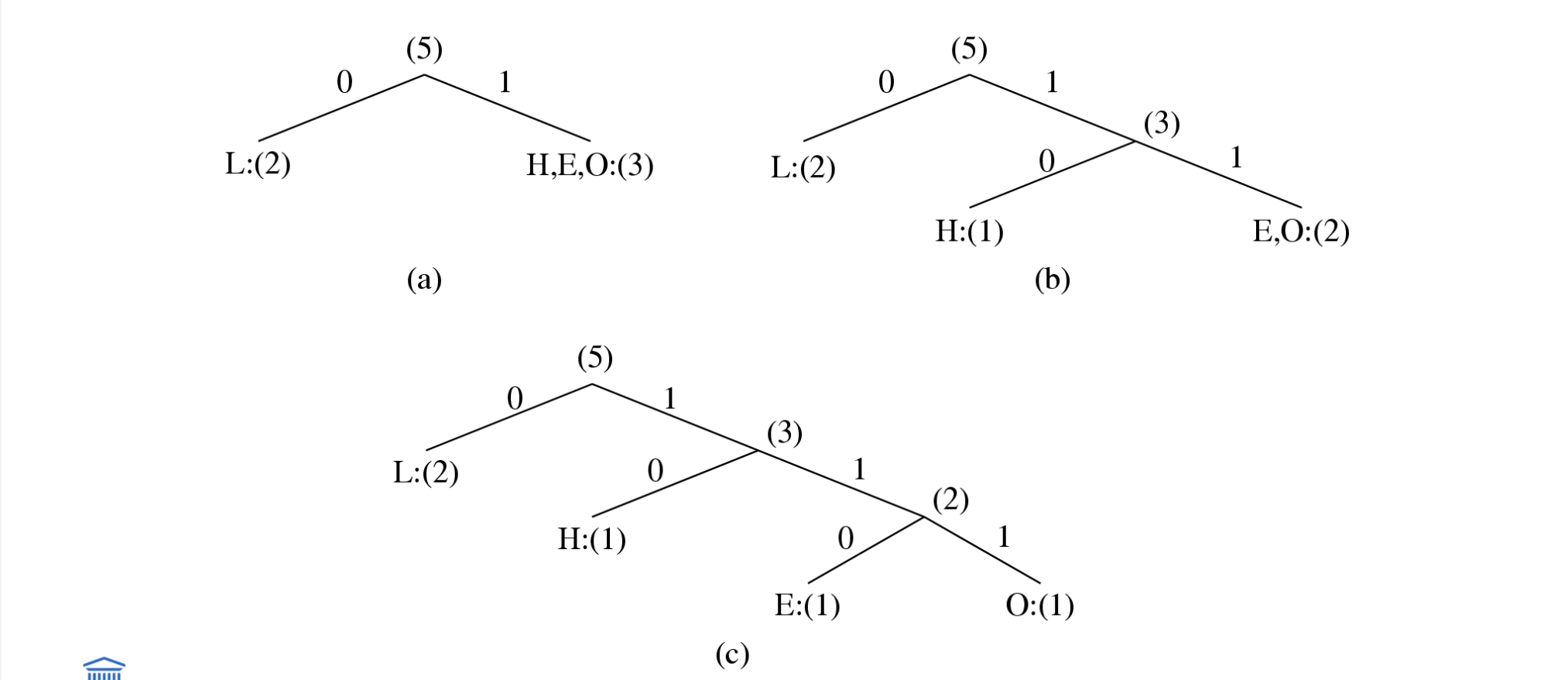
Boom 1

• L → 0

• H → 10

• E → 110

• O → 111

• Totaal bits: 10

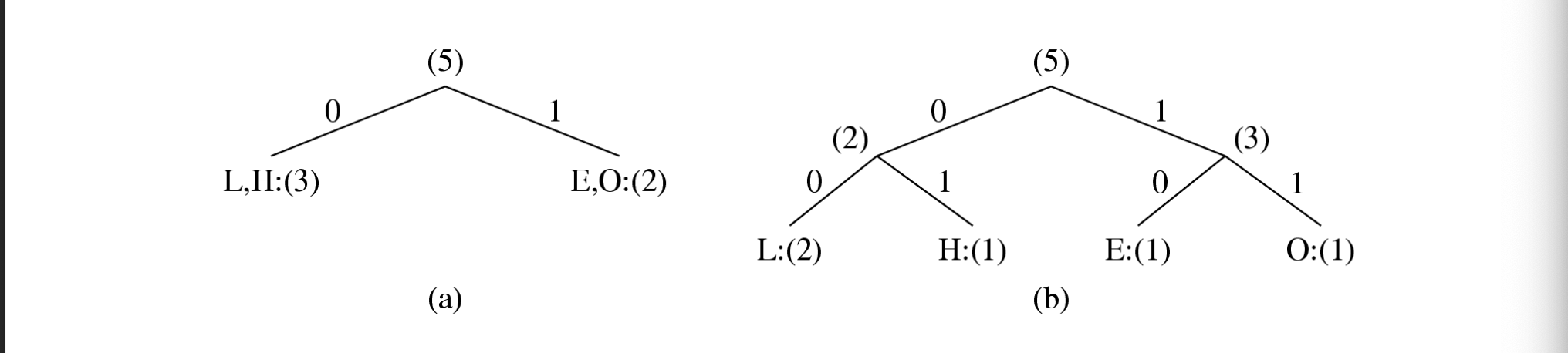
Boom 2 (slide 18)

• L → 00

• H → 01

• E → 10

• O → 11

• Totaal bits: 10

✔ Verschillende bomen mogelijk
✔ kan met ander totaal aantal bits
✔ Kortere codes voor frequentere symbolen

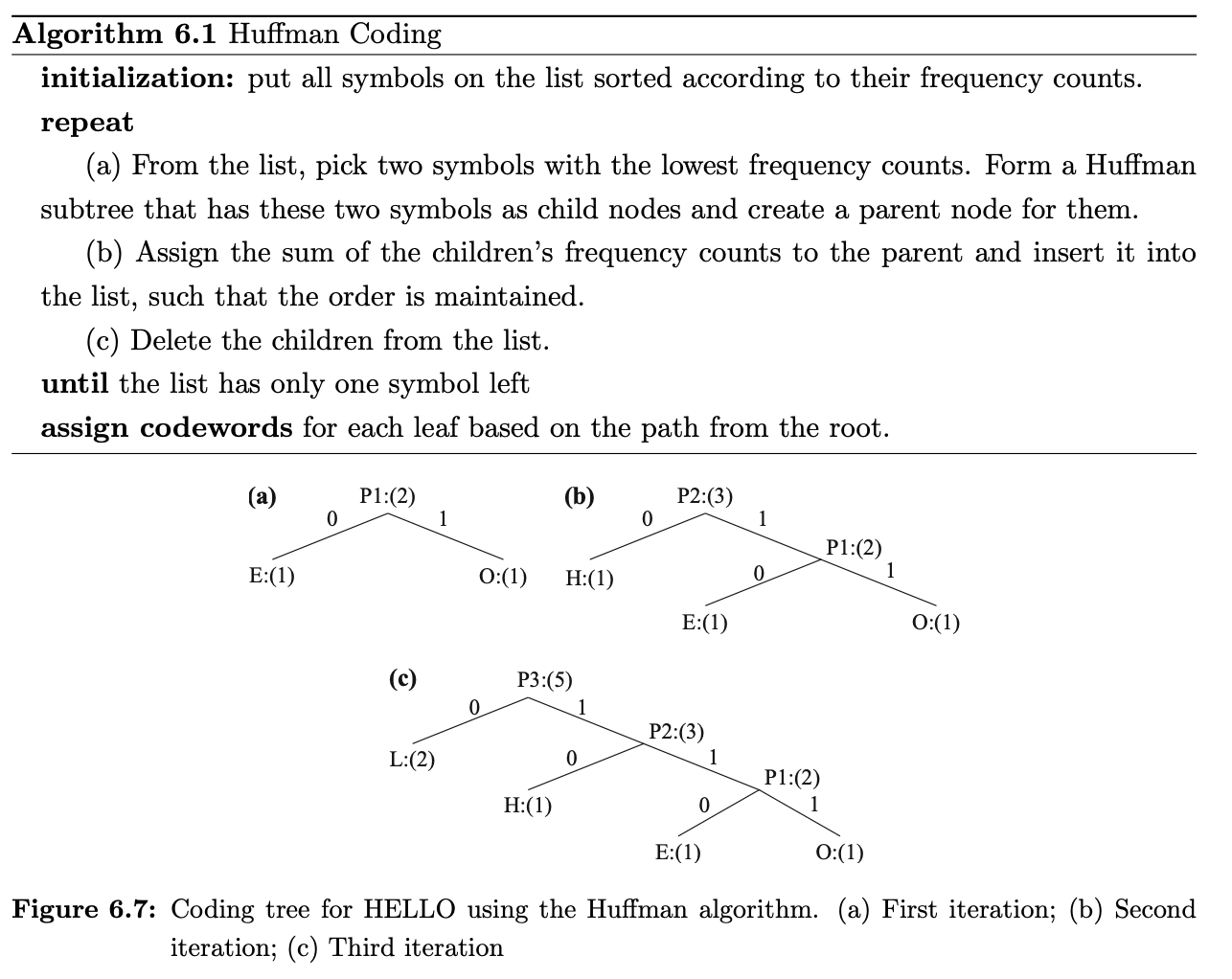
• huffman coding algorithm

• properties

Bottom-up aanpak

1. Initialisatie: zet alle symbolen op een lijst gesorteerd volgens frequentie

2. Herhaal tot de lijst slechts één symbool overhoudt:

   • kies de twee symbolen met de laagste frequentie; vorm een Huffman-subtree met deze twee als kindknopen en maak een ouderknoop

   • wijs de som van de frequenties van de kinderen toe aan de ouder en plaats die terug in de lijst zodat de volgorde behouden blijft

   • verwijder de kinderen uit de lijst

3. Wijs een codewoord toe aan elk blad, gebaseerd op het pad vanaf de wortel

• Unique Prefix Property: geen enkele Huffman-code is een prefix van een andere → geen ambiguïteit bij decoderen

• Optimaliteit: minimum-redundantiecode (bewezen optimaal voor een gegeven datamodel met bekende waarschijnlijkheidsverdeling)

  • de twee minst frequente symbolen hebben even lange Huffman-codes, alleen verschillend in de laatste bit

  • frequentere symbolen krijgen kortere codes dan minder frequente

  • de gemiddelde codelengte voor een informatiesource S is strikt kleiner dan η + 1

  

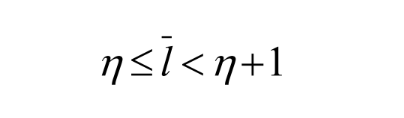
extended huffman coding

Extended Huffman Coding

• Motivatie:

  • alle codewoorden in gewone Huffman hebben een geheel aantal bits

  • wanneer de entropie om een bepaald symbool te coderen 0 nadert of gwn kleiner is dan 1 dan is het inefficient om dit symbool te coderen met een geheel aantal bits.

• Idee:

  • groepeer meerdere symbolen samen en wijs één codewoord toe aan de hele groep

  • bijvoorbeeld: voor alfabet S = {s₁, s₂, ..., sₙ}, als je k symbolen groepeert, dan krijg je een uitgebreid alfabet:
    S^(k) = {s₁s₁...s₁, s₁s₁...s₂, ..., sₙsₙ...sₙ}

  

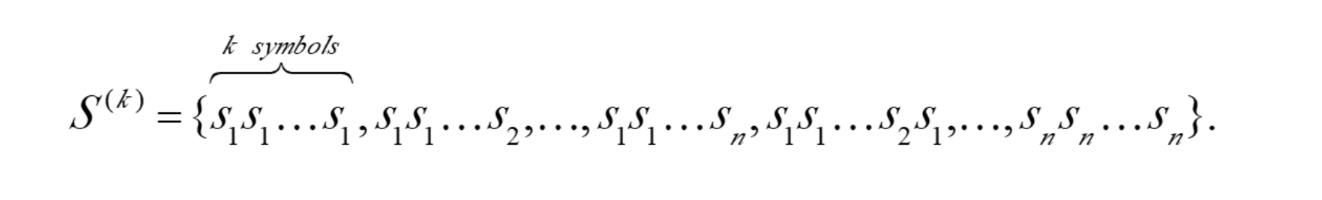
• Resultaat:

  • het gemiddelde aantal bits per symbool wordt:
    η ≤ l̅ < η + 1/k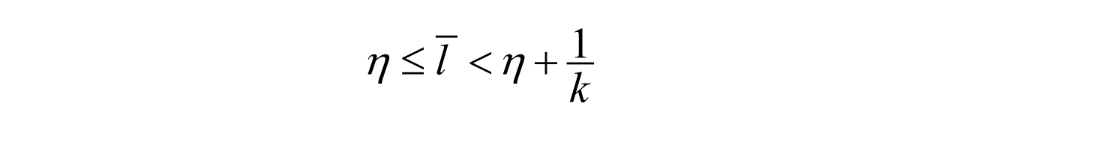

    

• Verbetering t.o.v. originele Huffman, maar niet heel groot

• Probleem:

  • als k groot is (bijv. k ≥ 3), dan wordt nᵏ te groot → enorme symbooltabel → onpraktisch in toepassingen waar n ≫ 1

adaptive huffman coding

Statistieken worden dynamisch verzameld en geüpdatet terwijl de datastroom binnenkomt

• Initial_code:

  • wijst symbolen toe met vooraf afgesproken codes

  • doet dit zonder vooraf kennis van frequenties

• update_tree:

  • bouwt een Adaptive Huffman-tree op

  • doet twee dingen:

    • verhoogt frequentietelling van symbolen (ook nieuwe)

    • past de boomstructuur aan

• Encoder en decoder:

  • moeten exact dezelfde initial_code en update_tree routines gebruiken

Notes over adaptive Huffman Tree Updating:

• Nodes worden genummerd: van links naar rechts, van onder naar boven (getallen in haakjes geven count aan)

• Boom behoudt altijd sibling property → alle nodes (intern en leaf) gerangschikt in toenemende count

• Bij schending van sibling property → swap-procedure activeert, herordent nodes

• Swap: verste node met count N wordt verwisseld met de node die net verhoogd werd naar N + 1

Arithmetic coding

• wat?

• verschil met huffman

• werking

Arithmetic Coding

• Moderne coderingsmethode, vaak beter dan Huffman

• Verschil met Huffman:

  • Huffman → kent elk symbool een eigen codewoord (hele getallen in bits) toe

  • Arithmetic → behandelt het volledige bericht als één geheel

• Werking:

  • Bericht voorgesteld als halfopen interval [a, b], met a en b ∈ [0, 1]

  • Startinterval: [0, 1]

  • Naarmate bericht groeit → interval wordt kleiner

  • Hoe kleiner interval, hoe meer bits nodig om het correct te representeren

  • proces herhaalt tot terminating symbol ontvangen wordt $

  • tag genereren: een nummer dat binnen de range valt

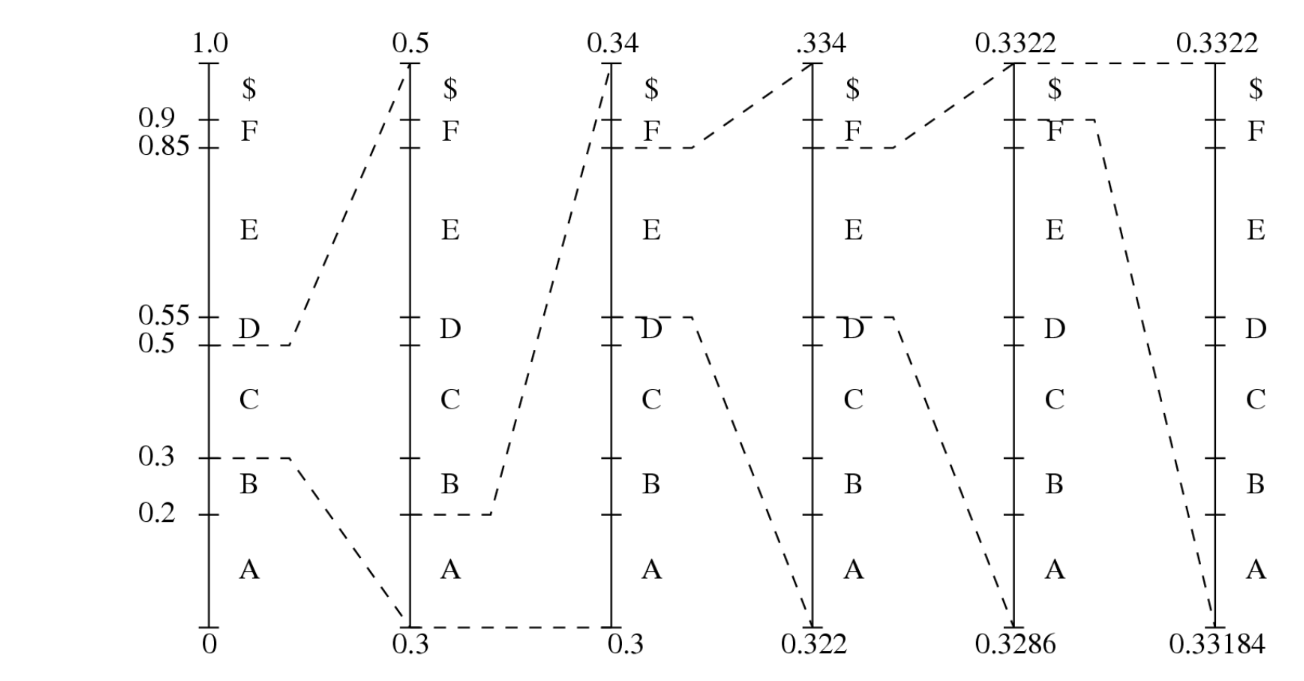
enkele problemen (2) en observaties (2) bij arithmetic coding

• Probleem bij basic arithmetic coding:

  • Lange sequenties → intervallen worden extreem klein → hoge precisie nodig

  • Geen output tot hele sequentie is ingevoerd → decoder heeft volledige codewoord nodig voor decoding

• Observaties:

  • Lage, hoge en willekeurige getallen in interval delen altijd dezelfde MSBs (Most Significant Bits)

    • vb. 0.1000110 voor 0.546875 (low), 0.1000111 voor 0.554875 (high)

  • Volgende intervallen blijven binnen huidig interval → we kunnen gemeenschappelijke MSBs meteen outputten en weglaten bij verdere verwerking

Verschillende soorten scaling bij arithmetic coding

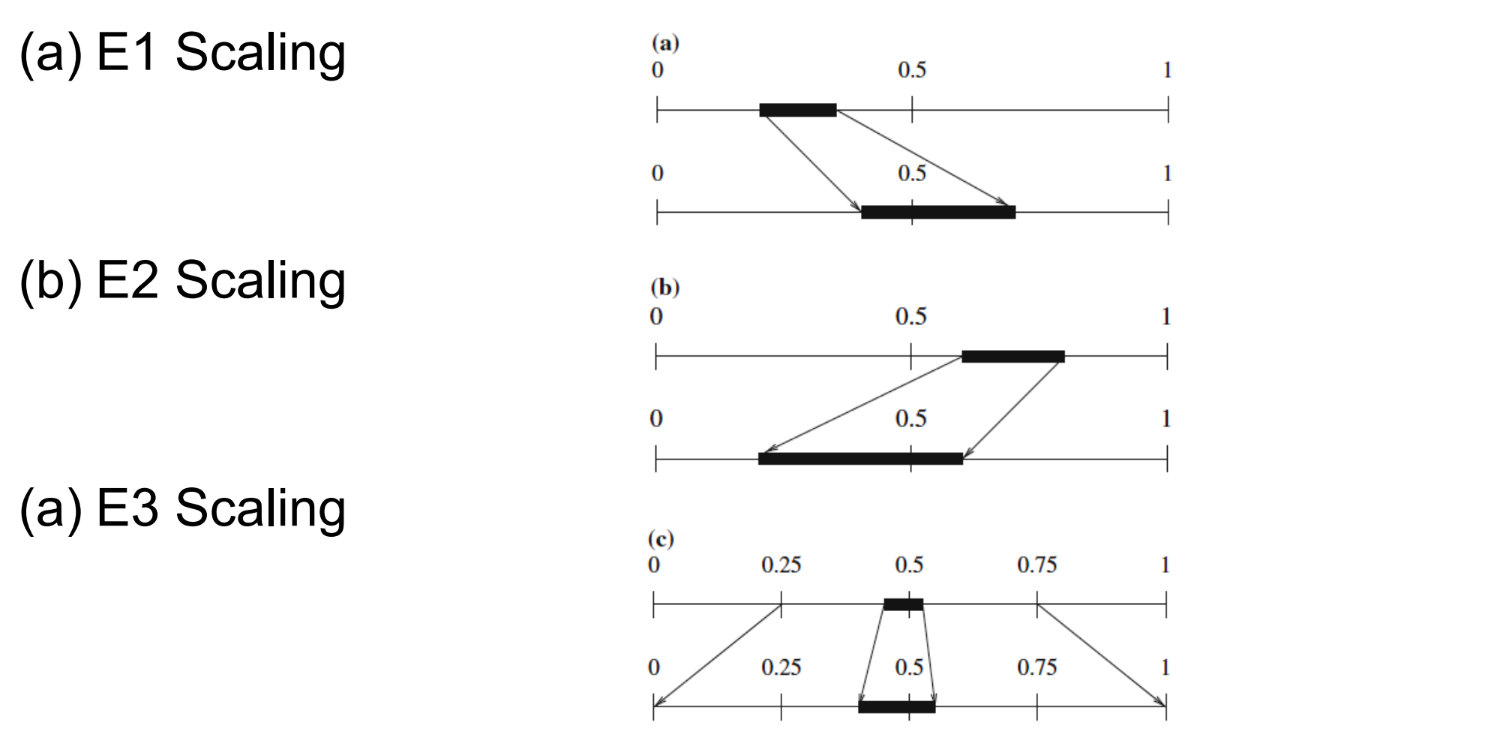
E1:

• huidig interval volledig in linkerhelft: laagste en hoogste waarde van interval maal 2 (bitshift left)

• high ≤ 0.5 → 0 naar de decoder sturen

• low = 2*low | high = 2*high

E2

• huidig interval volledig in rechterhelft: laagste en hoogste waarde van interval maal 2 en - 0.5 (bitshift left)

• low ≥ 0.5 → 1 naar de decoder sturen

• low = 2*(low-0.5) | high = 2*(high - 0.5)

E3

• One can prove that:

  • N E3 scaling steps followed by E1 is equivalent to E1 followed by N E2 steps

  • N E3 scaling steps followed by E2 is equivalent to E2 followed by N E1 steps

• Therefore, a good way to handle the signaling of the E3 scaling is: postpone until there is an E1 or E2:

  • if there is an E1 after N E3 operations, send ‘0’ followed by N ‘1’s after the E1;

  • if there is an E2 after N E3 operations, send ‘1’ followed by N ‘0’s after the E2.

integer implementation of arithmetic coding

Integer Arithmetic Coding

• Gebruikt alleen gehele getallen (geen floating points)

• Interval [0, 1] wordt vervangen door [0, N], bv. N = 255

• Kleine integer range vereist scaling-technieken (anders te weinig resolutie)

• Hoofdmotivatie: vermijden van floating point-operaties → efficiënter voor multimedia-applicaties

Binary arithmetic coding (BAC)

Binary Arithmetic Coding

• Gebruikt enkel binaire symbolen (0 en 1)

• Berekening van nieuwe intervallen en kiezen welk interval eenvoudiger

• Snelle varianten: Q-coder, MQ-coder (gebruikt in JBIG, JBIG2, JPEG-2000)

• Geavanceerd: CABAC (Context-Adaptive Binary Arithmetic Coding), gebruikt in H.264 (M-coder) en H.265

• Symbolen worden eerst gebinariseerd op een specifieke (geoptimaliseerde) manie

adaptive binary arithmetic coding

• houdt telkens bij hoeveel 0’en of 1’tjes al ontvangen werden en berekend zo de grootte van het interval

• wordt telkens aangepast per ontvangen bit (adaptive)

• voordeel tov adaptive huffman → geen nood aan zeer grote en dynamische symbol table

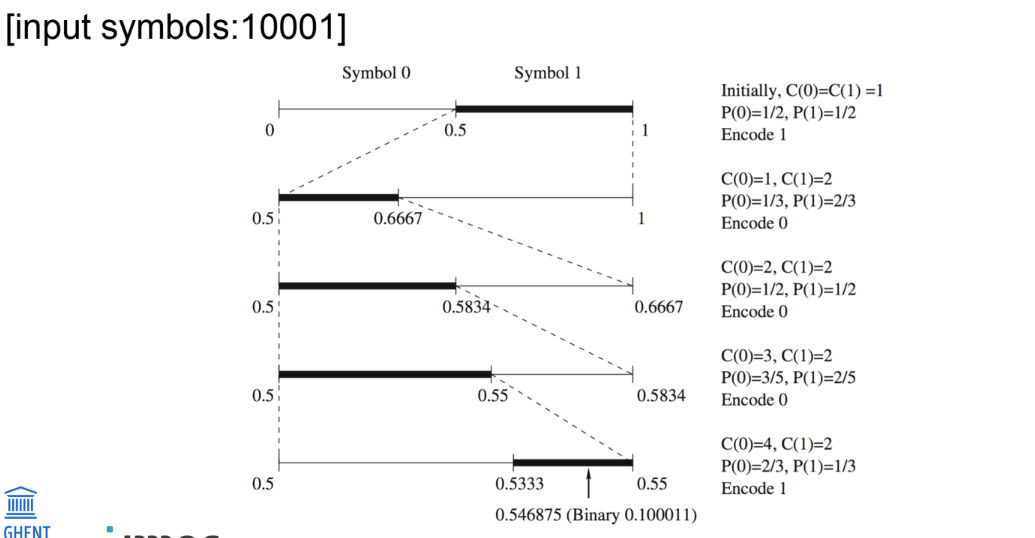
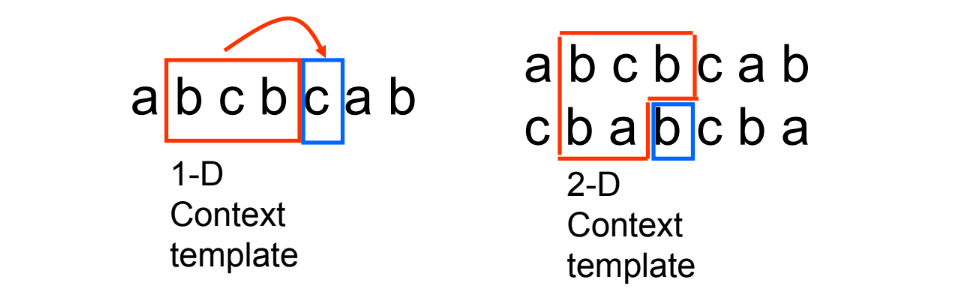
context-adaptive arithmetic coding

• Probabilities → higher-order models

• een sample heeft vaak sterke correlaties met zijn buren

• Contextmodellen (hoger-orde modellen)

  • Gebruik waarschijnlijkheden gebaseerd op naburige symbolen (context)

  • P( x(n) | x(n-1), x(n-2), … , x(n-k) )

  • Gebruik deze conditionele waarschijnlijkheid om het volgende symbool te coderen

  • Levert schevere (gewenste) verdelingen op → ideaal voor arithmetic coding

performance arithmetic coding vs huffman coding

■ Symbolen

• H(X) = entropie van de bron X (minimale gemiddelde bits per symbool)

• m = lengte van de sequentie

■ Arithmetic coding (over lengte m)

• H(X) ≤ Gemiddelde Bit Rate ≤ H(X) + 2/m

• Benadert de entropie zeer snel

■ Huffman-codering (over lengte m)

• H(X) ≤ Gemiddelde Bit Rate ≤ H(X) + 1/m

• Niet praktisch → je moet codewoorden genereren voor alle sequenties van lengte m

• Vergelijk: Extended Huffman coding

---

Simpel voorbeeld

• Stel bron X:

  • Symbolen {A, B} met P(A) = 0.8, P(B) = 0.2

  • Entropie H(X) ≈ 0.72 bits/symbool

Huffman (per symbool):

• A → 0

• B → 1

• Gemiddeld: 0.8 × 1 + 0.2 × 1 = 1 bit/symbool

Arithmetic coding (over sequentie “A B A”):

• Combineert alles tot één getal in [0,1], geen afronding per symbool

• Gemiddelde bit rate dichter bij 0.72 bits/symbool

Conclusie:

• Arithmetic coding benadert theoretische limiet sneller en efficiënter

• Huffman kan niet onder 1 bit/symbool tenzij je extended combinaties doet, maar dat wordt onpraktisch

Laat weten als je het uitgewerkt wil zien met tussenstappen!

differential coding of images

lossless image compression + distributions

Lossless Image Compression

• Differentiaalcodering van beelden:

  • Gebruik verschiloperator: d(x, y) = I(x, y) - I(x-1, y)

  • Of gebruik discrete 2D Laplace-operator: d(x, y) = 4I(x, y) - I(x, y-1) - I(x, y+1) - I(x+1, y) - I(x-1, y)

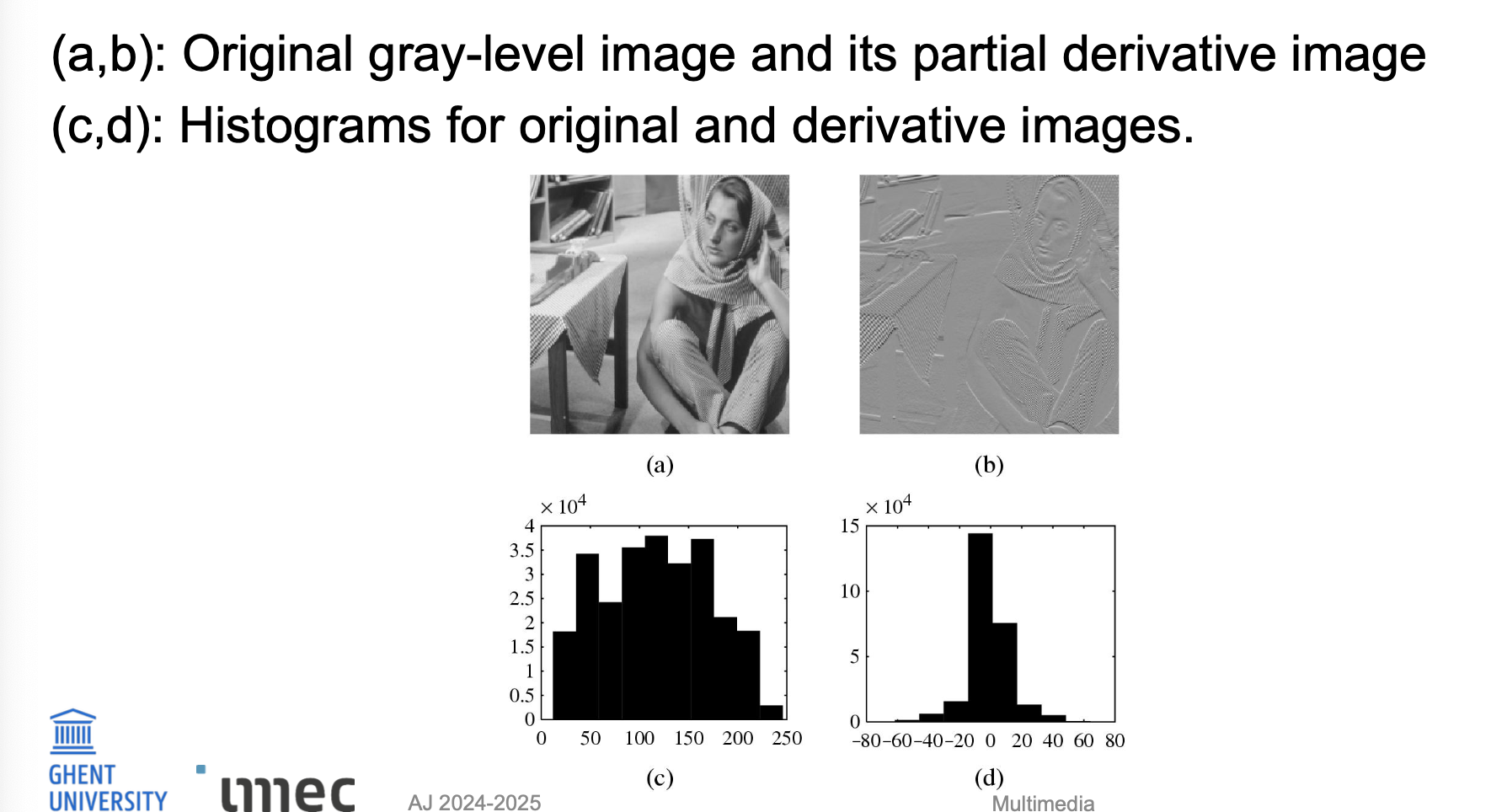
• Door ruimtelijke redundantie heeft verschilbeeld d een smaller histogram → lagere entropie (beter comprimeerbaar)

Distributies

• (a,b): origineel grijswaardenbeeld + partieel afgeleid beeld

• (c,d): histogrammen tonen dat verschilbeeld een smallere, scherpere verdeling heeft

Laat weten als je dit ook als korte vergelijking wil tussen de twee histogrammen!

lossless JPEG

Lossless JPEG (speciale modus JPEG-compressie)

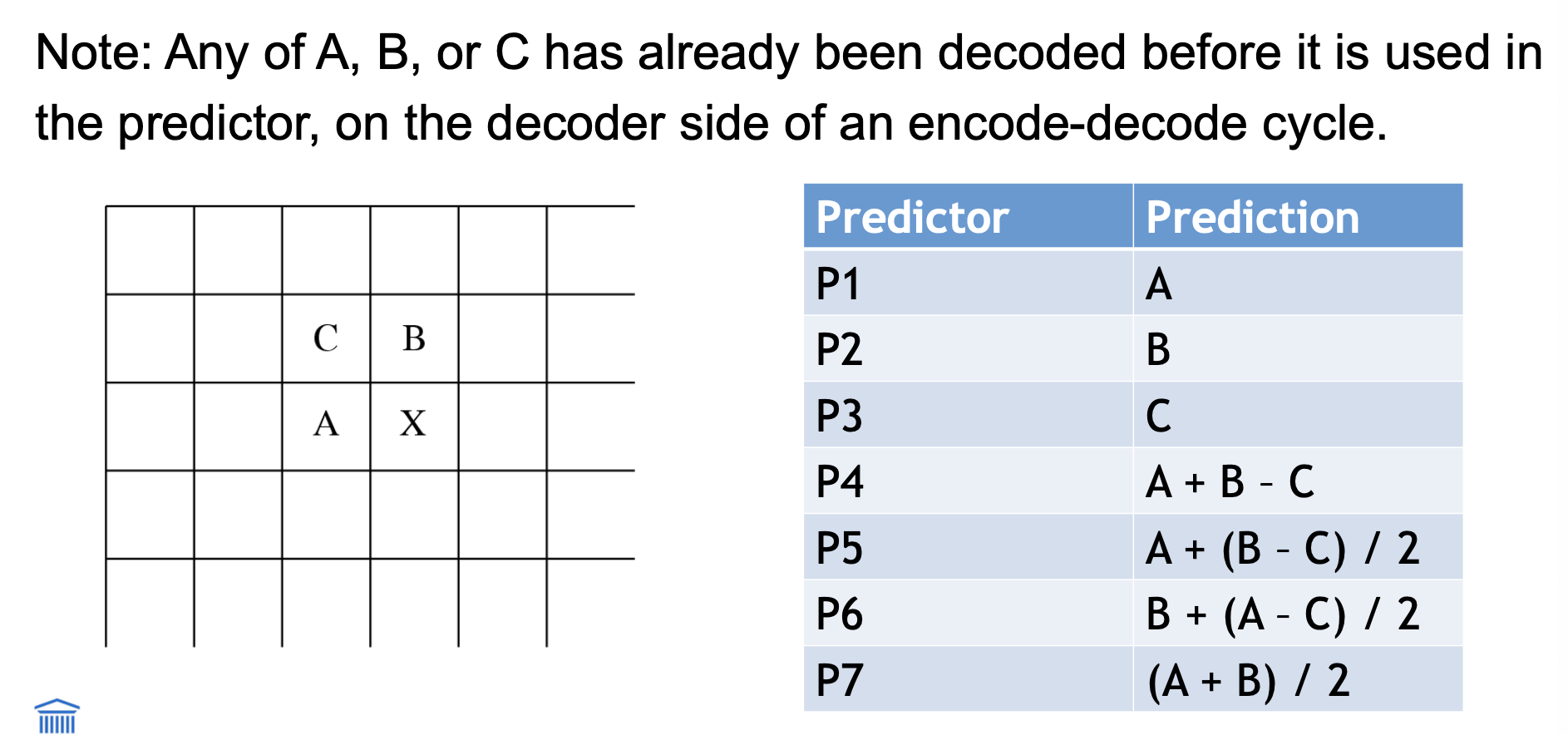
• Predictieve methode:

  • Vormt een differentiële voorspelling → combineert waarden van max. 3 naburige pixels als voorspelling voor huidig pixel (X)

  • Kan 1 van 7 voorspellingsschema’s gebruiken

• Codering:

  • Vergelijkt voorspelling met echte pixelwaarde op X

  • Codeert het verschil met verliesloze compressie (bijv. Huffman-codering)