A2 Maths Formulae

👍

\sec\left(x\right)=

\frac{1}{\cos\left(x\right)}

\operatorname{cosec}\left(x\right)=

\frac{1}{\sin\left(x\right)}

\cot\left(x)\right.=  

\frac{1}{\tan\left(x\right)}

How many degrees in 2π ?

360

Multiply x^{\omicron} by ___ to get the angle in radians

Arc length (RADIANS ONLY)

θr

Sector area (RADIANS ONLY)

\frac12\theta r^{2}

How to work out segment area?

Sector area - Triangle area

\sin\left(\theta\right)\thickapprox

\theta

\cos\theta\thickapprox

1-\frac12\theta^{2}

\tan\theta\thickapprox

\theta

IDENTITY: \tan\theta=

\frac{\sin\theta}{\cos\theta}

IDENTITY using \sin\left(x\right), \cos\left(x\right) and 1

\sin^2\left(x\right)+\cos^2\left(x\right)=1

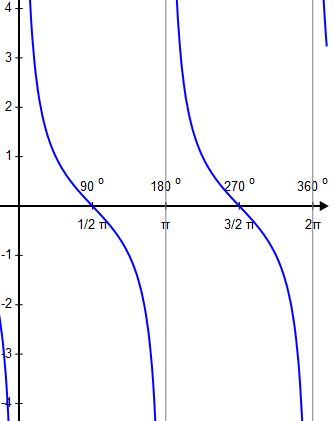
What graph is this?

y=\cot\left(x\right)

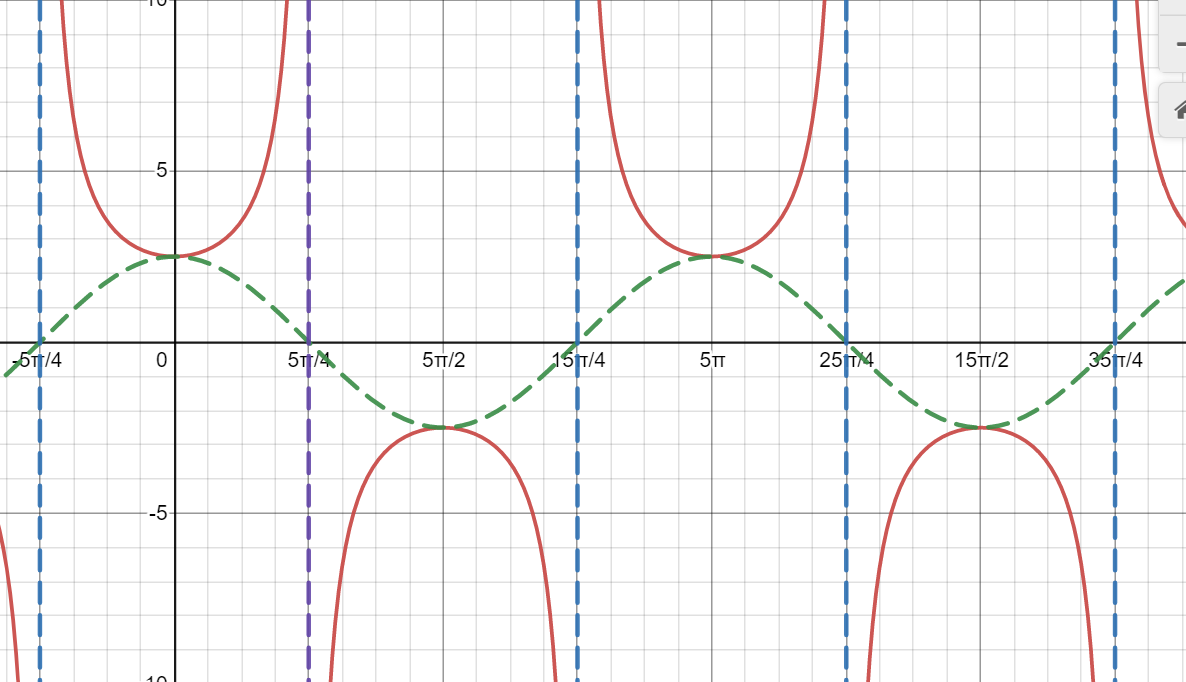
What graph is this?

y=\operatorname{cosec}\left(x\right)

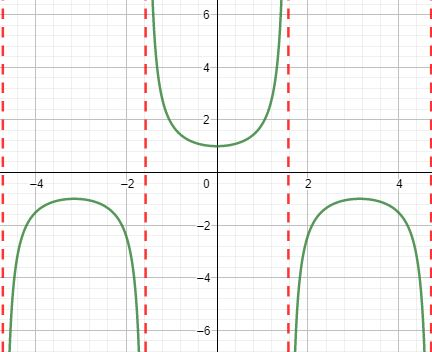
What graph is this?

y=\sec\left(x\right)

IDENTITY (there’s 3): \cos\left(2\alpha\right)

1-2\sin^2\left(\alpha\right),2\cos^2\left(\alpha\right)-1,\cos^2\left(\alpha\right)-\sin^2\left(\alpha\right)

IDENTITY: \sin\left(2\alpha\right)

2\sin\left(\alpha\right)\cos\left(\alpha\right)

IDENTITY: \tan\left(2\alpha\right)

\frac{2\tan\left(\alpha\right)}{1-\tan^2\left(\alpha\right)}

\cos\left(\alpha+\beta\right)=

\cos\left(\alpha\right)\cos\left(\beta\right)-\sin\left(\alpha\right)\sin\left(\beta\right)

\sin\left(\alpha+\beta\right)=

\sin\left(\alpha\right)\cos\left(\beta\right)+\cos\left(\alpha\right)\sin\left(\beta\right)

\tan\left(\alpha+\beta\right)=

\frac{\tan\left(\alpha\right)+\tan\left(\beta\right)}{1-\tan\left(\alpha\right)\tan\left(\beta\right)}

\sin\left(\alpha-\beta\right)=

\sin\left(\alpha\right)\cos\left(\beta\right)-\cos\left(\alpha\right)\sin\left(\beta\right)

\cos\left(\alpha-\beta\right)=

\cos\left(\alpha\right)\cos\left(\beta\right)+\sin\left(\alpha\right)\sin\left(\beta\right)

\tan\left(\alpha-\beta\right)=

\frac{\tan\left(\alpha\right)-\tan\left(\beta\right)}{1+\tan\left(\alpha\right)\tan\left(\beta\right)}

a\sin\left(\theta\right)+b\sin\left(\theta\right)=

R\sin\left(\theta+\alpha\right)

a\sin\left(\theta\right)-b\sin\left(\theta\right)=

R\sin\left(\theta-\alpha\right)

S_{n}=

\frac{a\left(1-r^{n}\right)}{1-r}

S_{\infty}=

\frac{a}{1-r}