data reduction

data types

• Nominal e.g. fluvial or answer to yes or no Q

• Ordinal - e.g. 1,2,3

• Continuous - interval and ratio e.g. mass, time, concentration, distance

• scalar - isolated value that represents something e.g. height or weight

internal data

differences between measurements, but no true zero

ratio data

differences between measurements, the true zero exists

raw data

• can not manage

• difficult to see patterns

• need to process it

• use descriptive stats e.g. most common value

data assessment

min, max, range, middle values ?

plot data

outliers ?

trends/patterns ?

frequency data - histograms

how many of each value / class in the sample

for nominal and ordinal data - counting occurrences

frequency distribution - what is the shape ?

central tendency

middle values

dispersion

how spread are the values

central values

most useful if distribution is peak-shaped - cluster around centre

unimodal distributions are common

most values - central values - some variation on either side e.g. height

measures of central tendency

median, mode, mean

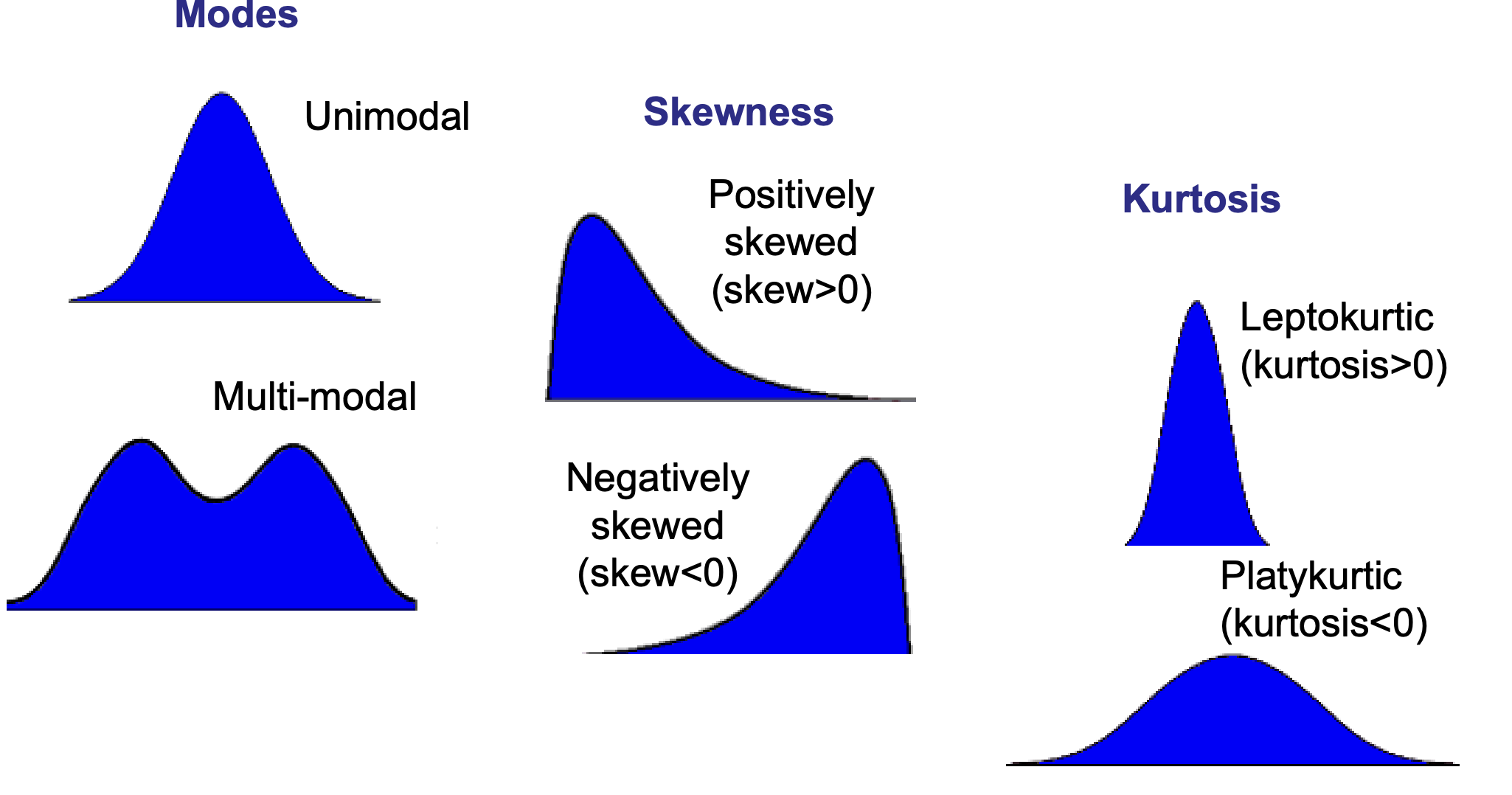
relationship of mean, median and mode

symmetrical unimodal distribution

mean = median = mode

non-symmetrical (skewed - unimodal distribution of values

leptokurtic = more than 0

platykurtic = less than 0

measure of dispersion when using media

interquartile range

measure of dispersion when using mean

standard deviation

interval scale data

unimodal

comparing standard deviations - coefficient of variation

useful if 2 values have 2 different means or 2 different scales

to do this divide standard deviation by mean then multiply by 100 for both samples

see which one has more variation - the one with higher percentage

moments of distribution

moments are indicators if the distribution shape - linked by powers of differenced

the s on the pic = standard deviation

uncertainty

measurements naturally lead to uncertainty

unavoidable

include uncertainty estimated

weighing provides a measure of importance

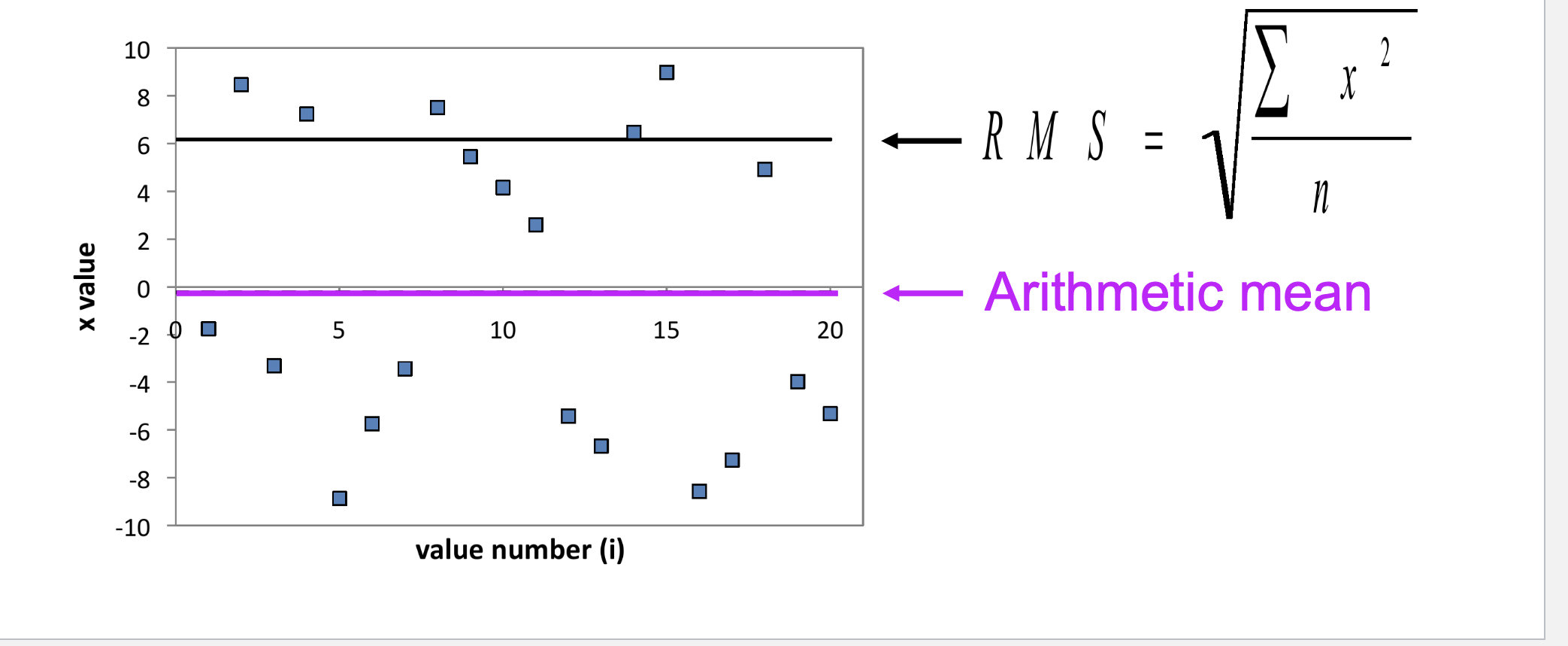
root mean squared

if values fall above and below zero - will be in the middle of the values

sometimes useful to know absolute magnitude of the values - how far the values are from 0

rms - achieves this by taking the average of the squared values