geometrie - teil 3 - metrik und anordnung

Definition Metrik

Es seien X eine Menge und d : X × X → R eine Abbildung mit folgenden Eigenschaften:

Symmetrie: ∀x, y ∈ X : d(x, y)= d(y, x),

positive Definitheit: ∀x, y ∈ X : d(x, y) ≥ 0,

∀x, y ∈ X : d(x, y)= 0 ⇐⇒ x = y,

Dreiecksungleichung: ∀x, y, z ∈ X : d(x, y) ≤ d(x, z)+ d(z, y).

Dann heißen d Metrik, Distanz oder Abstand auf X und (X,d) metrischer Raum.

Definition Diskrete Metrik

Für jede Menge X ist die Abbildung d : X × X→ R mit

∀x, y ∈ X : d(x, y) := 0, falls x = y,

1, falls x ̸= y,

eine Metrik auf X .

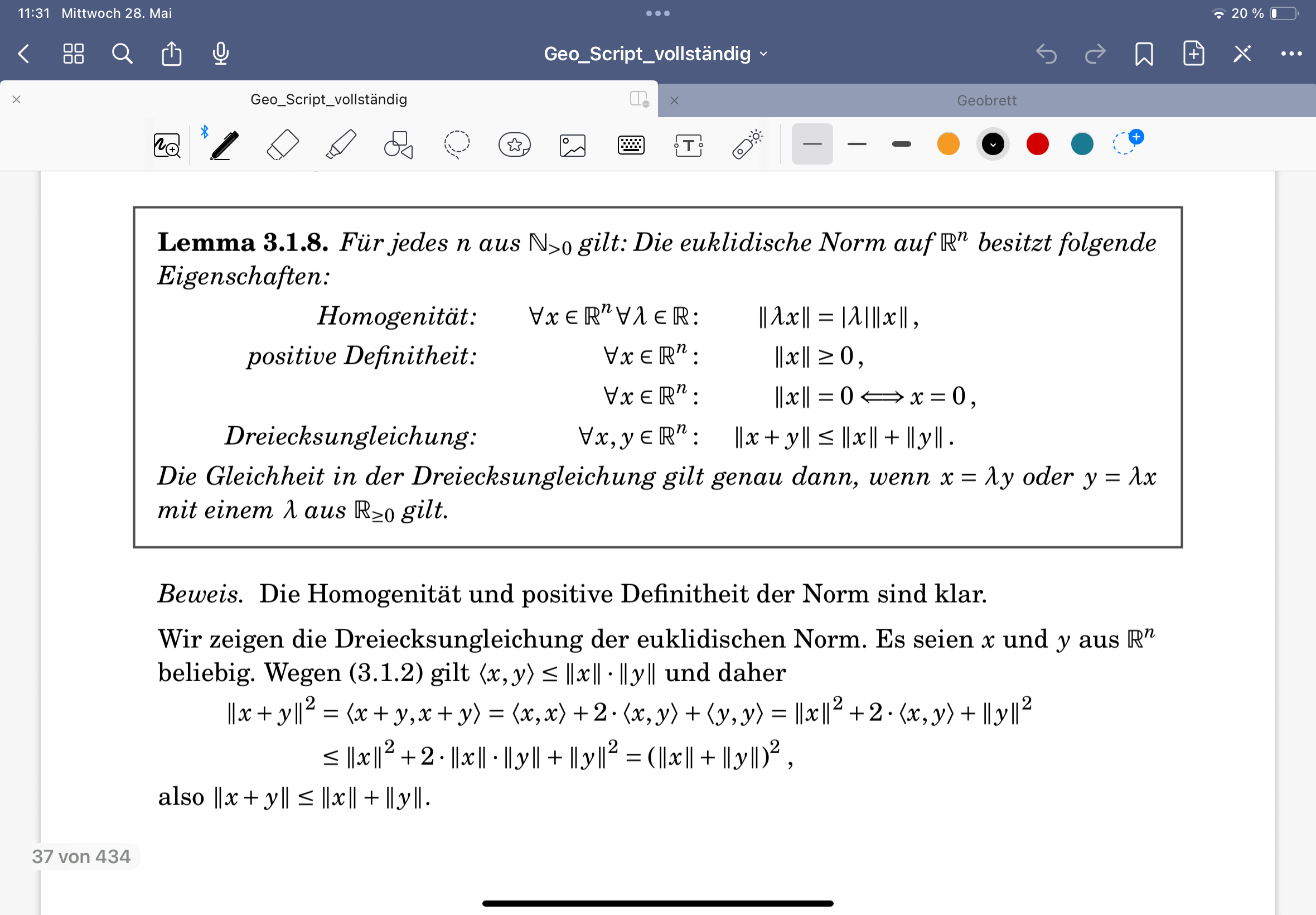
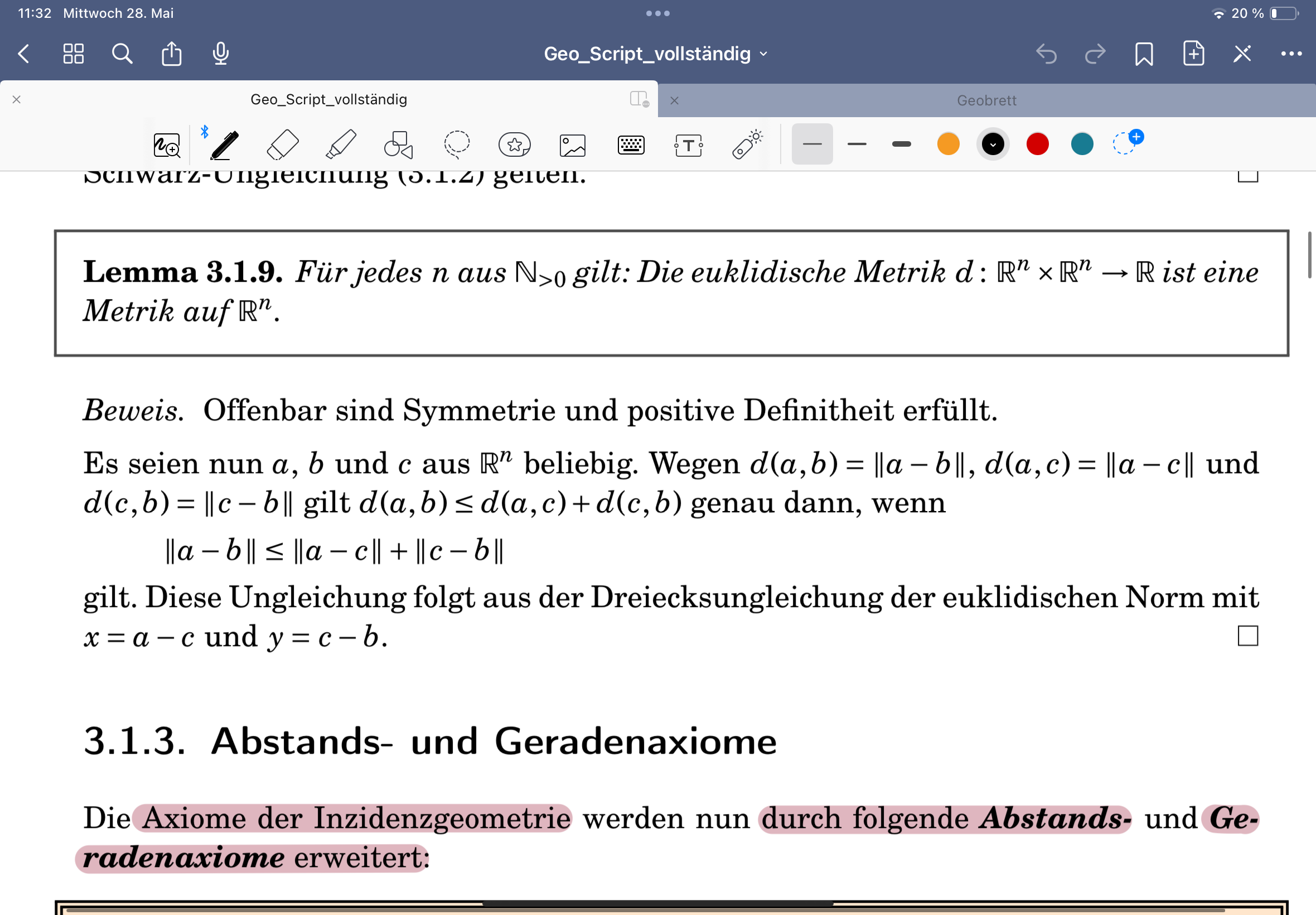
Euklidische Metrik

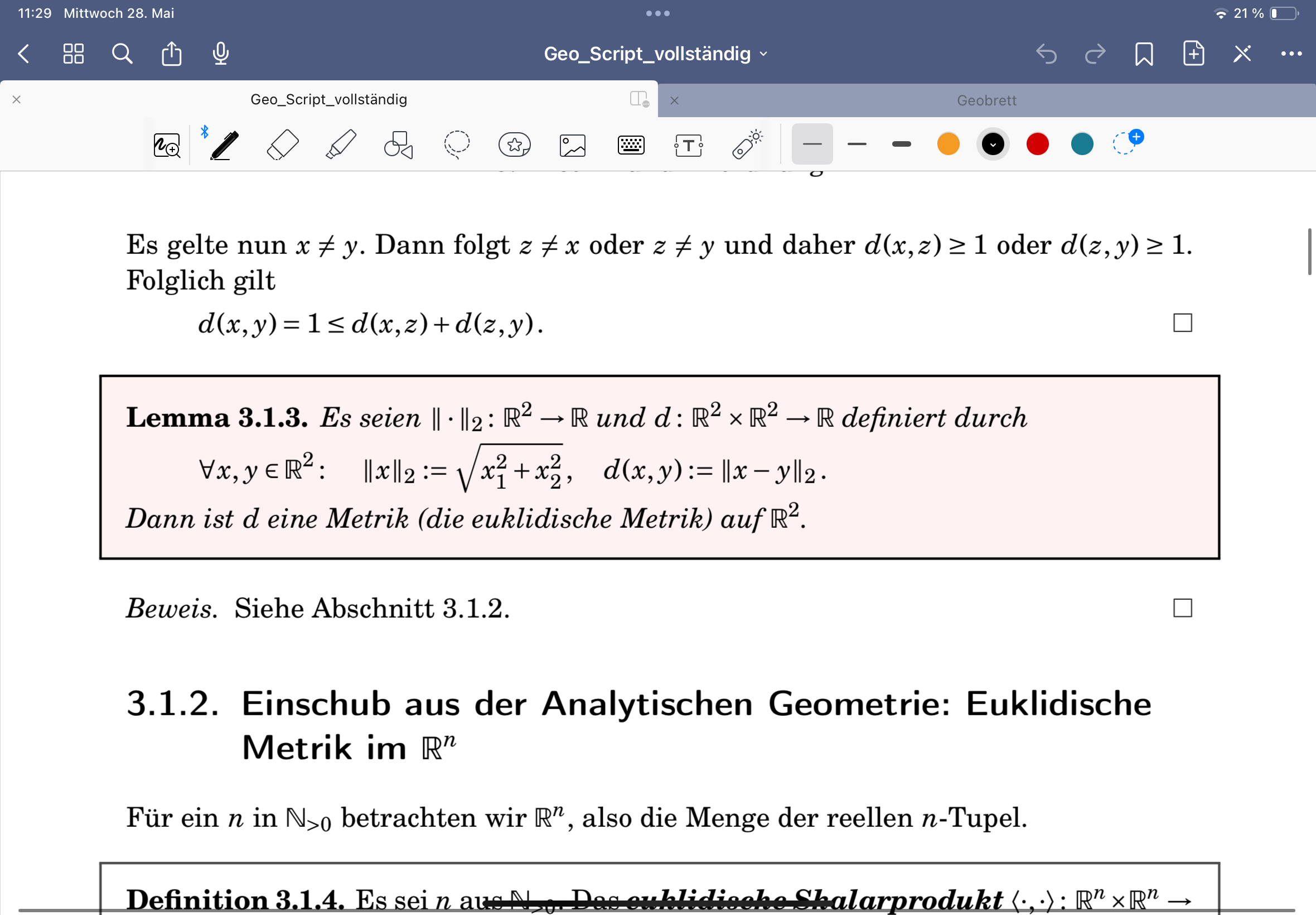
Euklidische Metrik in R^n

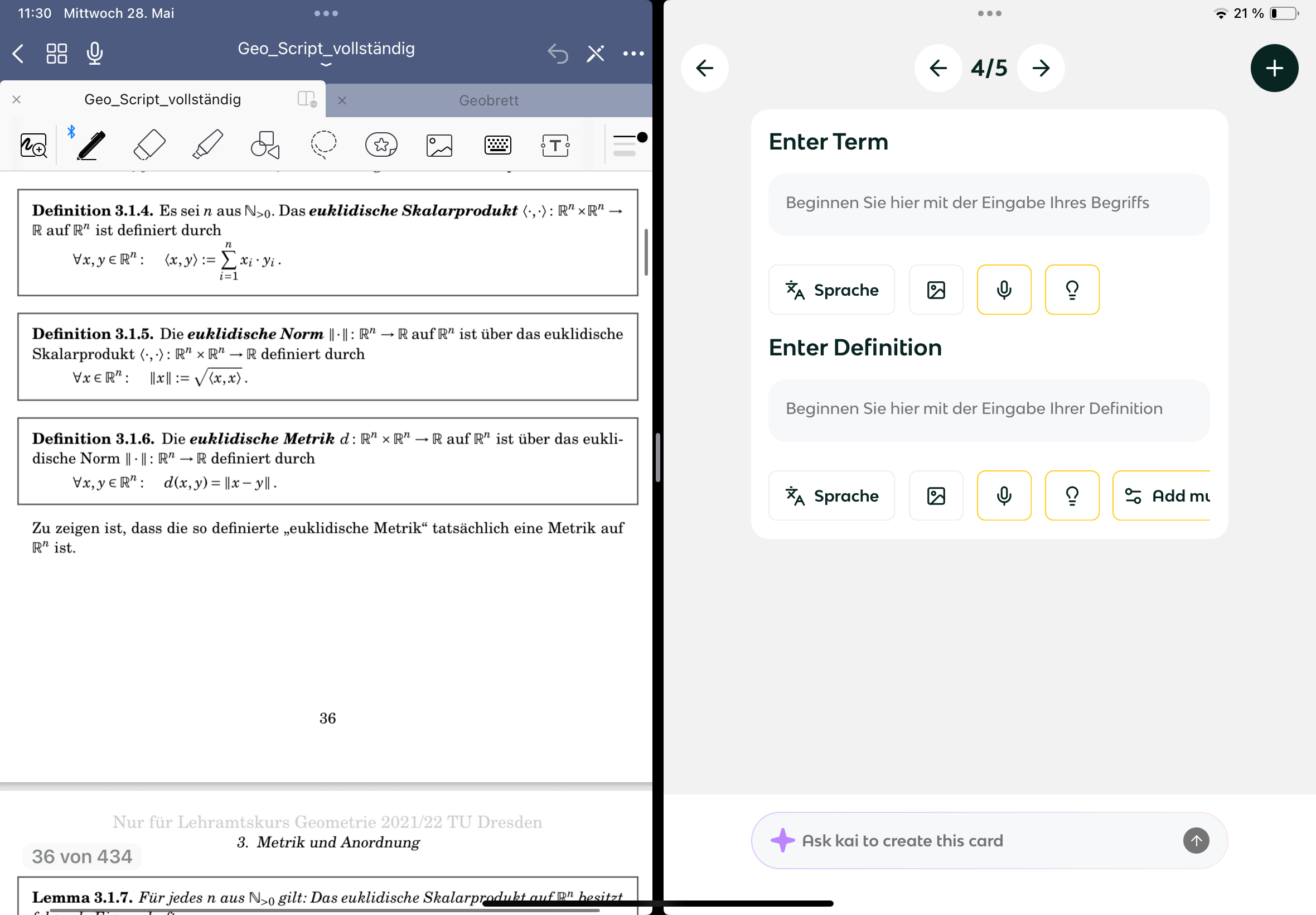
Eigenschaften euklidisches Skalarprodukt auf R^n

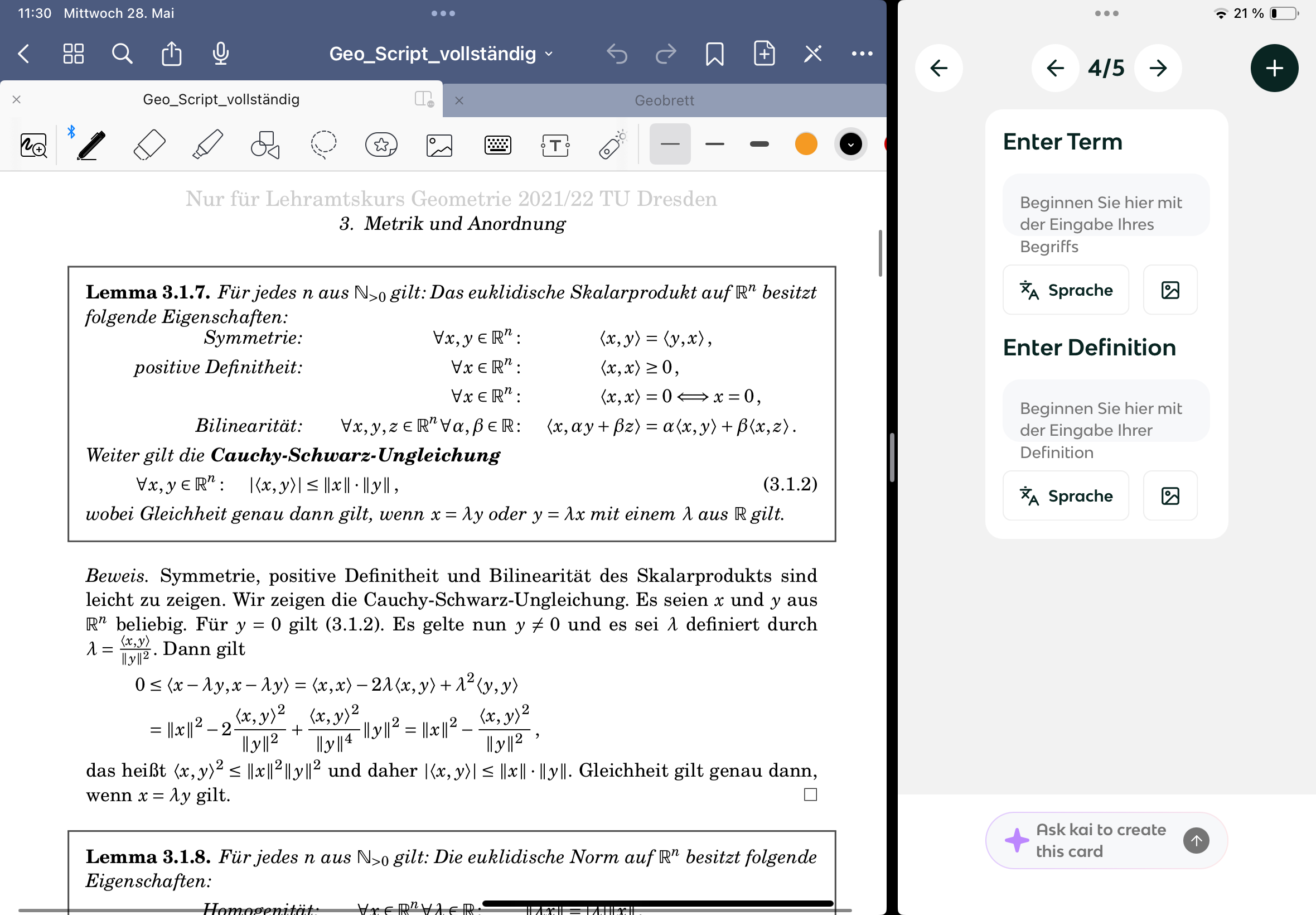
Eigenschaften euklidische Norm

Axiom Metrik

Es gibt eine Metrik d : P × P→ R auf P.

Geradenaxiom 1

Drei Punkte A, B , C aus P liegen genau dann auf einer Geraden aus G, wenn eine der Gleichungen

d(A,C )= d(A,B )+ d(B ,C ),

d(A,B )= d(A,C )+ d(B ,C ),

d(B ,C )= d(A,B )+ d(A,C )

gilt.

Definition Zwischenrelation

Auf der Menge der Punkte P wird die dreistellige Relation Zw ⊂ P × P × P definiert durch

(A,B ,C ) ∈ Zw :⇐⇒ A,B ,C ∈ P ∧ A ̸= B ̸= C ̸= A ∧ d(A,B )+ d(B ,C )= d(A,C ).

Sie wird Zwischenrelation genannt.

—

Ein Punkt B liegt zwischen den Punkten A und C , wenn (A,B ,C ) ∈ Zw. Weiter definieren wir

A−B−C :⇐⇒ (A,B ,C ) ∈ Zw.

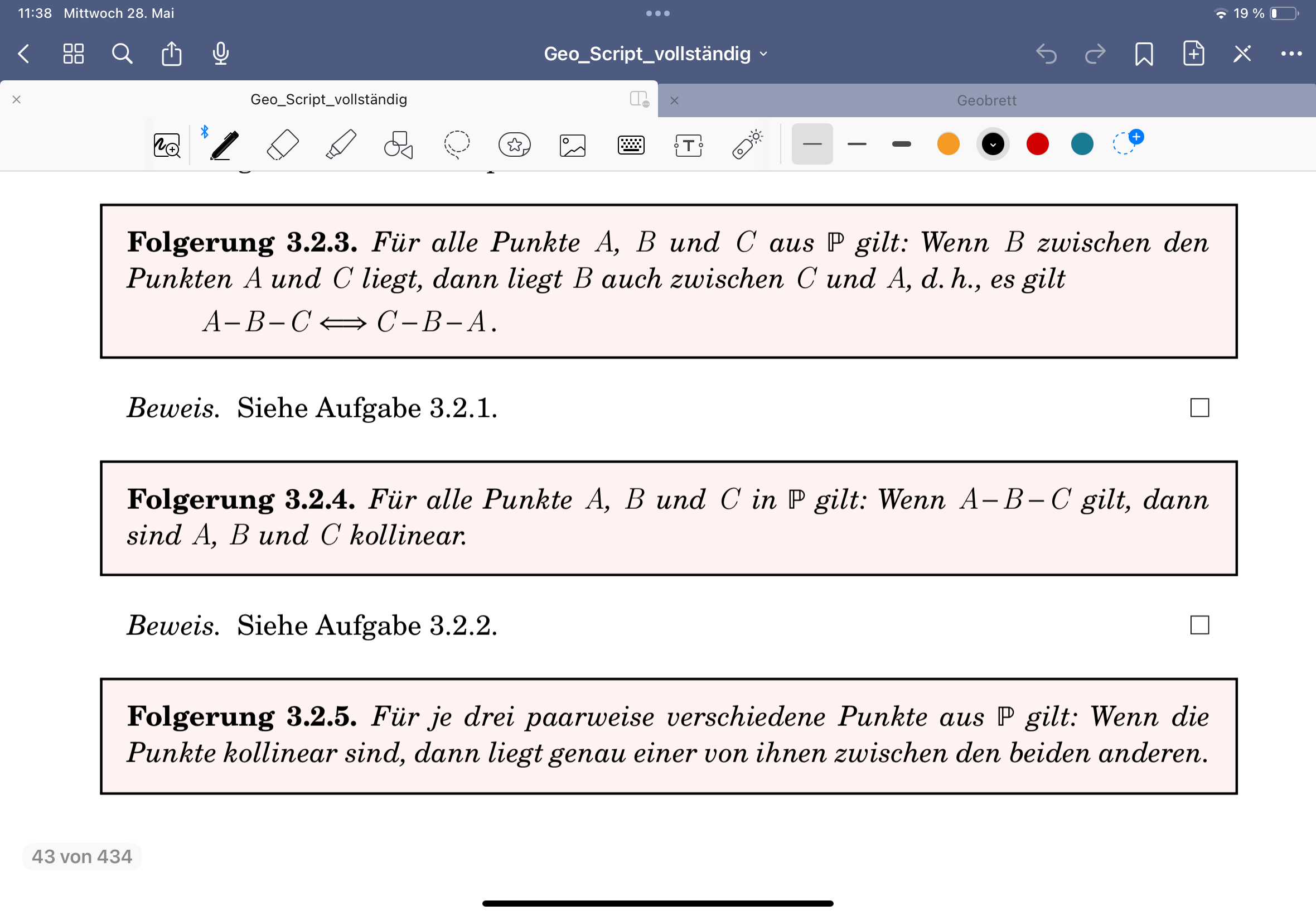
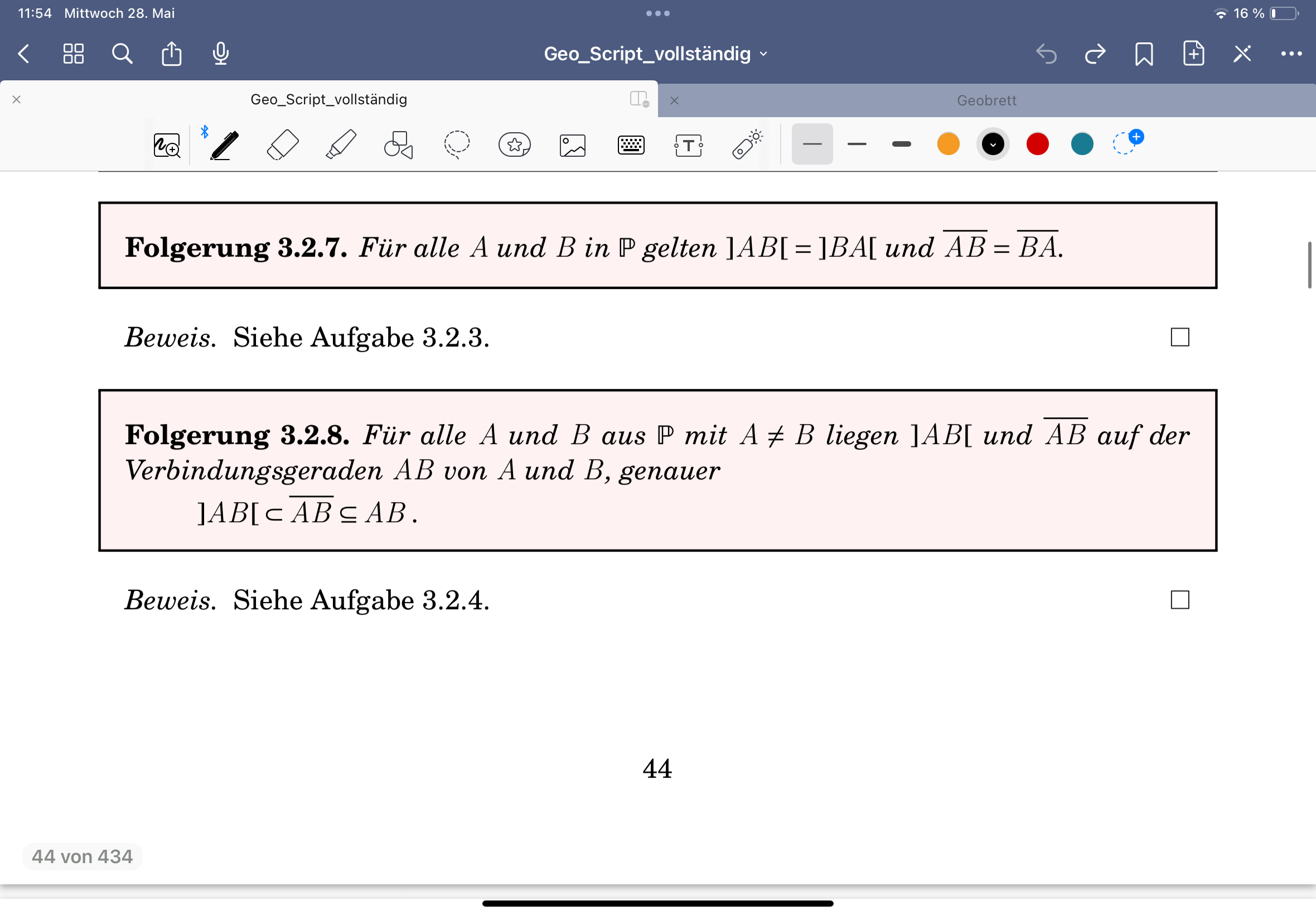
Folgerungen aus Zwischenrelation

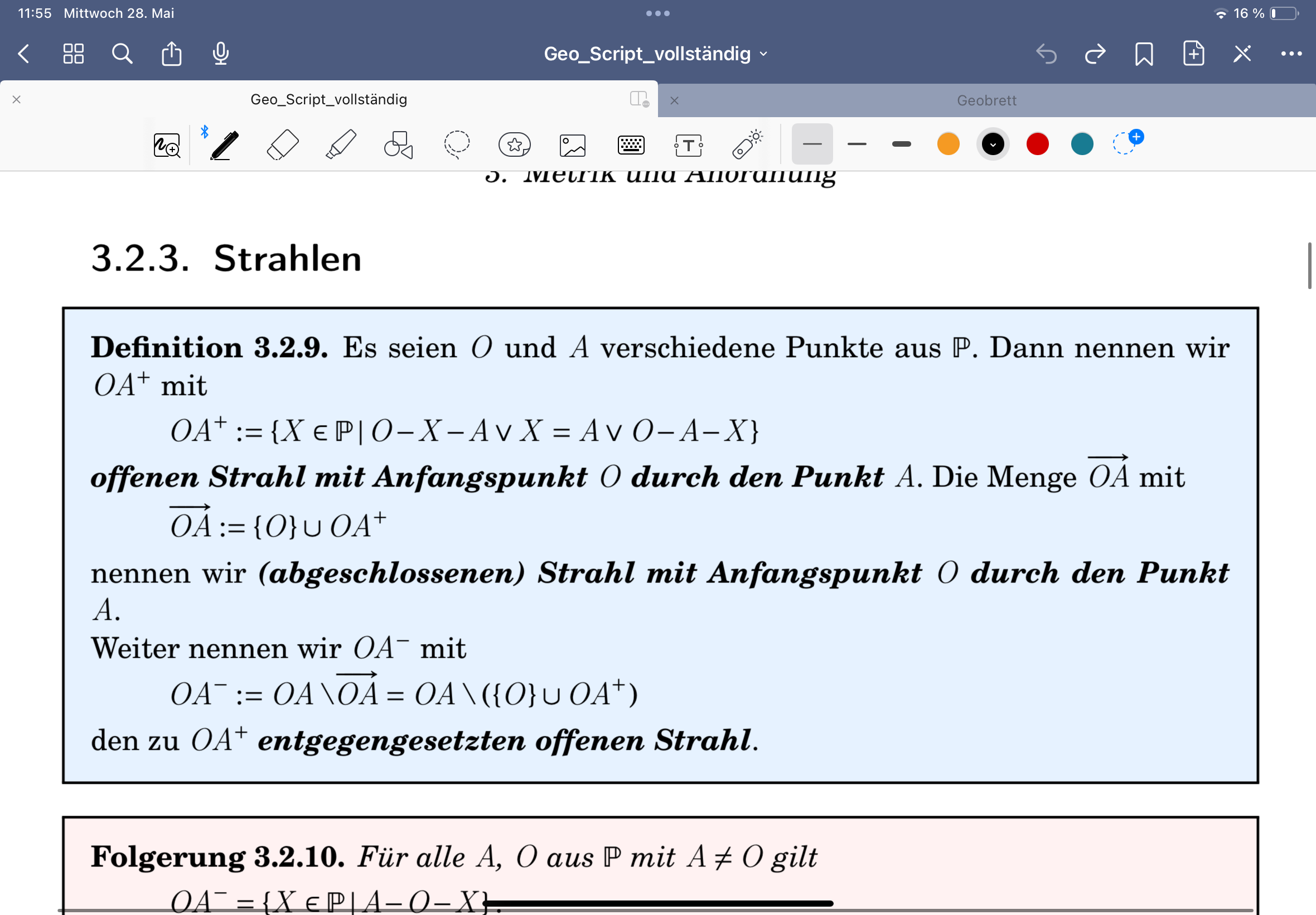
Definition Strecke

Es seien A und B aus P. Dann heißt

]AB [ := {P ∈ P | A−P−B }

offene Strecke mit den Endpunkten A und B . Die Menge

AB := [AB]= ]AB[ ∪ {A,B}

heißt abgeschlossene Strecke, kurz Strecke mit den Endpunkten A und B. Die Strecke AB heißt auch Verbindungsstrecke der Punkte A und B. Die Länge der Strecke AB ist der Abstand der Punkte A und B und wird mit |AB| bezeichnet, d. h. |AB| := d(A,B).

Definition Strahlen