Chem 101: Unit 1 Atoms

What formula is used to calculate the energy of stationary states?

En=-RH(Z²/n²)

What does Z indicate?

Atomic number

What does n mean (stationary state)

n is equal to the number of stationary state (1,2,3... to infinity)

What is RH

The Rhydberg constant 2.179 x 10^-18 J

The formula En= -RH(Z²/n²) is only applicable to what type of species?

One-electron

Examples of one-electron species include;

H, He+, Li2+

What is the stationary state of an electron?

Electrons do not radiate energy as they orbit or circle the nucleus, instead they exist in stationary states- a state of constant energy.

What do stationary states imply?

That electrons orbit at a fixed distance from the nucleus

Ground state

n=1

First excited state

n=2

second excited state

n=3

How does energy change from one state to another?

The n=1 state has the lowest energy, the energy increases by a big gap to the n=2 state. The n=2 to n=3 transition is also an increase, but with a smaller gap this time, the energy continuosly increases by progressively smaller gaps

n=infinity

The electron has become free and the hydrogen-like species is now ionized

When will a photon of energy be emitted?

When an atom in an excited state (n=2 - n=infinity) relax to a lower energy state

Energy of a photon is equal to

the difference in energy between the higher and lower states of the electron

The formula Ephoton(or delta E)=hc/λ is used to calculate

the energy of a photon of the difference of energy between stationary states

The planck constant (h) is equal to

6.626 x 10^-34 Js

The speed of light constant (c) is equal to

2.998 x 10^8 m/s

An electron undergoing a transition with a large energy difference produces a photon with a __________ wavelength

short

An electron undergoing a transition with a small energy difference produces a photon with a __________ wavelength

long

The longest wavelength emitted is from the transition between

n=2 to n=1

the shortest wavelength emitted is from the transition between

n=infinity to n=1

wavelength (λ) and energy are ___________ related

inversely

The balmer series has an n final of

2

the lyman sereies has an n final of

1

Since the smallest energy corresponds to the largest wavelength the same energy transition will be seen as a line on the far _____ of the plot.

right

Since the largest energy corresponds to the shortest wavelength the same energy transition will be seen as a line on the far _____ of the plot

left

The Bohr's model is limited to describing the spectra of

Hydrogen like species (one-electron species)

To find a hydrogen-like species, use the expression

E^ +(Z-1), ie. He--> Z-1=2-1= He+

Be Z=4 so Be^(4-1)= Be3+

How do you find the change in energy (delta E)

Use the Rhydberg equation: (delta E) = -RH x Z² ((1-nf²)-(1/ni²))

In the Rhydberg equation, if yoou want to find Z instead of Delta E, what should you do?

Replace Delta E with the energy, if you are provided with a wavelength instead of energy use the formula Delta E=hc/λ to find it then substitute

When calculating make sure that the

units line up. (all lengths are in metres, energy in J or KJ)

In an emission transition the energy is

negative

In an absorption transition the energy is

positive

Wavefunction is symbolized by

𝚿 (psi)

What is the wavefunction?

3D coordinates that have been obtained by solving the Schrodinger equation

What are the two parts of the wavefunction?

Radial (r) and Angular (Y), wavefunctions for singular electrons can be referred to as orbitals

Each solution of the Schrodinger equation yields

the energy state associated with a given atomic orbital

Probability Density is represented by

𝚿²

Probability density is

the probability of finding an electron in some tiny volume of the atom

In a probability density DOT diagram, gretaer density represents

a higher probability of finding the electron in that volume

Radial probability distribution

represents the total probability density at some distance (r) from the nucleus

Total electron density peaks _____ but not _____ the nucleus

near, at

Probability contour

the shape that defines the volume around the nucleus within which an electron spends a given percentage of its time

The 1s orbital has ___ nodes

no nodes

A node on a probability density plot is represented by

a zero (the y-coordinate touches the x-axis)

On a density probability plot, a maxiumum represents

A distance at which the probability of finding an electron is high

In a 3D distribution plot, the white rings represent

nodes

Because a 2s orbital is bigger, an electron spends more time ______ from the nucleus than in a 1s orbital

away

# of radial nodes=

n-ℓ-1

Quantum numbers

specify the properties of atomic orbitals and the properties of electrons in orbitals

Principal quantum number

symbolized by n, indicates the main energy level occupied by the electron and the size of the orbital

angular momentum quantum number

symbolized by ℓ, indicates the shape of the orbital

Magnetic Quantum number

symbolized by mℓ, indicates the orientation of an orbital around the nucleus (spacial orientation)

n= a level so ℓ=

a sublevel

ℓ=0

s orbital

ℓ=1

p orbital

ℓ=2

d orbital

ℓ=3

f orbital

ℓ is an integer from 0 to n-1

The number of possible values of ℓ=n

mℓ is an integer from

-ℓ through zero to +ℓ

-ℓ,(-ℓ+1),0,....ℓ

total number of mℓ values =

2ℓ +1

If n=1 and ℓ=0 then mℓ has to be

equal to zero

if n=2 then ℓ can equal:____, ____,

0,1

If n=2 and ℓ=1 then mℓ can equal: ____, ____,____.

-1,0,1

The total number of mℓ values for a given n value=

n², which equals the total number of orbitals in that energy level

When ℓ= 0 there is only one value for mℓ, so that means there is only

one "s" orbital

When l=1 there are three possible values for mℓ, which means there are

3 "p" orbitals

How many d orbitals are there?

five

How many "f" orbitals are there?

7

How many electrons are in the "s" orbital?

2 electrons

How many electrons are in the "p" orbital

6 electrons

Which orbital has 10 electrons

the "d" orbital

How many electrons in the "f" orbital?

14 electrons

How many orbitals in an atom can have the following designation: n=3

To solve this, you want to use the formula to calculate the total number of mℓ values which is n², so in this case 3²=9

In an orbital diagram, two arrows pointing in different directions represent

a pair of electrons

how many electron pairs can fit in the 1s orbital?

1 (up, down)

How many electron pairs can fit in a 2s orbital?

1 (up, down)

How many electron pairs can fit in a 2p orbital?

3 (up down, up down, up down)

Hund's Rule

When orbitals of equal energy are availible, maximize unpaired electrons.

How does Hunds rule apply to an orbital diagram?

When you don't have enough electrons to fill all of the orbitals in pairs, it means that the electrons will spread out over the orbitals before pairing up.

Example of Hund's Rule

Carbon: fill as many orbitals as possible before pairing electrons on the valence orbital

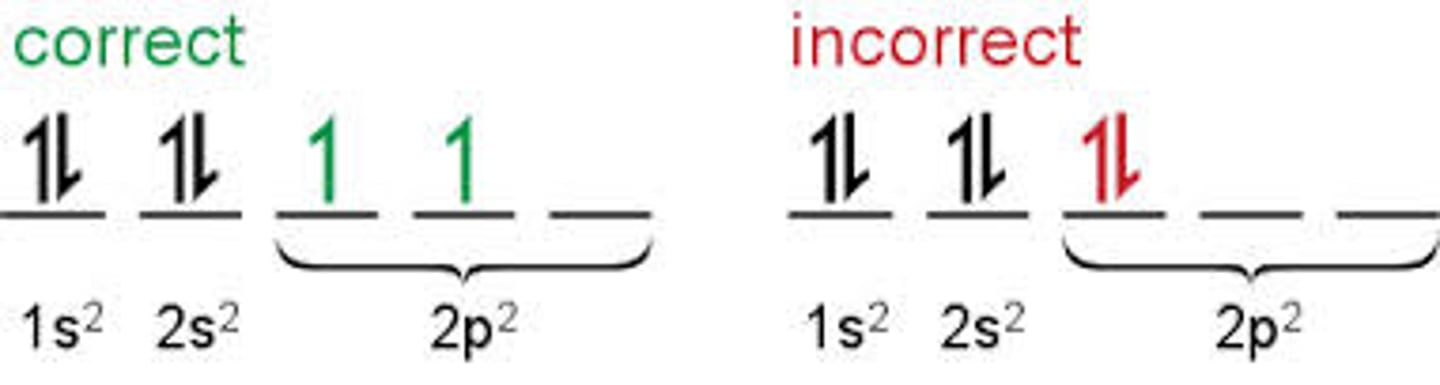
The 2p has 3 orbitals, what subscripts would be used to identify them?

X,Y and Z (2px, 2py, 2pz)

What is the spdf notation for Boron?

1s² 2s² 2p^1

What is the spdf notation for oxygen?

1s² 2s² 2p^4

Core electrons

same as their preceeding noble gas

Valence electrons

electrons that go beyond their preceeding noble gas core

Condensed notation

involves using the noble gas before the element to represent the core, then using regular spdf notation to represent the valence electrons

Condensed notation for Mg

[Ne] 3s²

Condensed notation for S

[Ne] 3s² 3p^4

In condensed notation, n= period numbe, therefore Lithum is

[He] 2s^1 because Li is in the 2nd period

Elements in the same group have the same valence electron configurations, and thus

similar chemical behaviour

For neutral atoms, the 4s orbital is ________ in energy than the 3d orbital

lower

Chromium and Copper Exception

Copper and Chromium do not follow the regular method for detecting configurations

Condensed configuration of Copper (Cu)

[Ar] 4s1 3d10

Condensed configuration of Chromium

[Ar] 4s1 3d5

Why are copper and chromium exceptions?

Because chromium orbital configuration has completely half-filled orbitals, and Copper has all fully filled 3d orbitals, which are more stable than their expected configuration

s block elements include

Groups 1 and 2 +helium

d block elements include

all the transition metals, groups 3-12

p block elements include

the mettaloids and non-metals (groups 13-16 -helium