algebra:

• Subtraction & addition-consider like terms

• cancellation: only works for factors

• when expanding, apply foil (if it is a binomial) or go from left to right

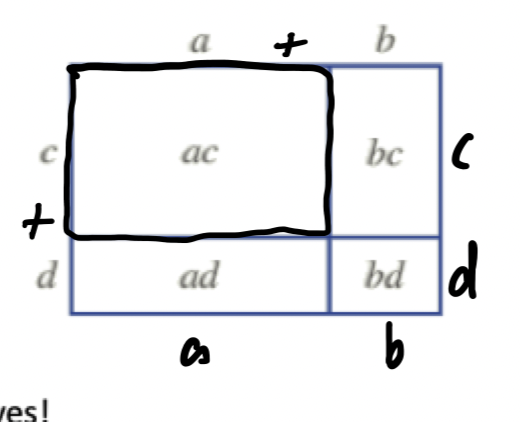
• Factorise by: HCF, grouping,

indices:

• when working with indices, start from the inside out

• Base is the big number, index/power is the small one on the upper righthand side

• anything to the power of 1 is equal to itself

• prime factorisations involve writing out a factor tree to sum up the prime factors of a number (both LCM and HCF)

• If bases are the same, add together the powers when multiplying

• If bases are the same, subtract together the powers when dividing

• If a base is to the power of 0 (zero), it equals to 1

• The base cannot be 0 for powers of 0 = undefined

• When raising a term (in brackets), keep the base and multiply indices

  • eg; (3³)⁸ = 3³ˣ⁸ = 3²⁴

• When indices are applied to fractions with brackets, apply the power to the top and bottom

• negative index: must put in reciprocal before solving

  • x⁻¹ = ⁠1/x⁠

  • reciprocal: flipped version of number

Equations:

• equation: and expression with an equal sign

• Have to rearrange equations so then the variable is on one side (LHS OR RHS)

• Check by substitution

• When moving across equal sign, do the opposite operation

• If variables on both sides, group them to one side like ‘like terms‘

• Steps to solve word equations:

  • Read the question

  • Define pronumeral (eg; Let x be the number of…)

  • Write equation

  • Solve equation

  • Answer question in words

  • Check if it makes sense (subbing in equation, checking if its supposed to be positive or negative…)

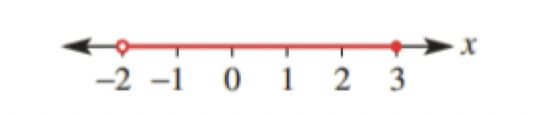
• Inequalities

  • the bigger side of a sign is pointing to the bigger number

  • close circles include (its including the hole in the middle)

  • open circles exclude (O for open)

    

• Quadratics are equations where highest power is 2

  • basic form ax²=c

  • always 2 solutions when the number is greater than or equal to 1(positive or negative)

  • always 1 solution when the answer is 0

  • always 0 solutions when the answer is negative

  • leave answers in surd form

  • When a binomial = 0, the two solutions are the numbers with their sign flipped

    • eg; (x-4)(x-5) = 0. solutions are x=4, x=5

• Cubics

  • basic form ax³=c

  • don’t need to worry about +-

Trigonometry:

• Pythagoras: a²+b²=c²

• Trigonometric Ratios:

  • theta: the angle you are trying to find

    • opposite: opposite theta

    • hypotenuse: opposite right angle

    • adjacent: next to theta

      

  • sin θ = opposite/hypotenuse (SOH)

  • cos θ = adjacent/hypotenuse (CAH)

  • tan θ = opposite/adjacent (TOA)

  • when finding unknown sides, sub in to find pronumeral

  • when finding unknown angles, use inverse sin/cos/tan to find theta

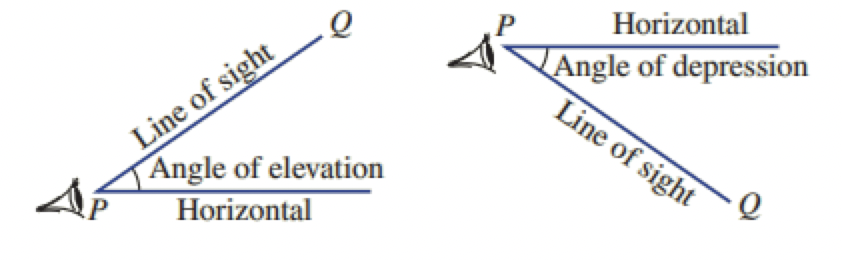
  • angles of elevation and depression are equal due to alternate angles

    

• Bearings

  • compass bearings - two compass directions (n/s and w/e) and an acute angle in the middle (WHICH IS ALWAYS MEASURED TO THE VERTICAL aka N/S)

  • true bearings - three digit clockwise system (eg; 273˚, 090˚)

  • always use arrows for bearings so you know what direction

  • eg; A from O is an arrow going from point O to A