Standard scores

Standard Scores Definition

A raw score converted to another scale with a set mean and standard deviation.

Standard Scores Purpose

Makes scores easier to interpret; shows performance relative to others.

Standard Score Benefit

Helps compare test-takers fairly across different tests/scales.

z score

• Mean = 0

• Standard Deviation (SD) = 1

• Shows how far and in what direction a raw score is from the mean in SD units.

T score

• Mean = 50

• SD = 10

• Always positive, avoids negative numbers.

Stanines

• Mean = 5, SD ≈ 2

• Range: 1 to 9 (whole numbers only)

• Each stanine = ½ standard deviation wide

• 5th stanine = average (middle 20% of scores)

• 4th & 6th stanines capture about 17% each below/above average

• Commonly used in achievement tests in schools

What is a z score?

A z score indicates how many standard deviations a raw score is above or below the mean.

Formula for calculating a z score?

• X = raw score

• Xˉ\bar{X}Xˉ = mean

• sss = standard deviation

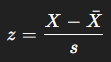
What does a z score of +1 mean in terms of percentile?

About 84% scored equal or below, only ~16% scored higher.

Why are z scores better than raw scores?

They provide context:

• Show relative standing in the distribution.

• Allow comparison between different tests/scales.

Example of comparison across tests (Crystal’s case)?

• Reading raw = 24 → z = +1.32 (above average).

• Arithmetic raw = 42 → z = –0.75 (below average).
  → Even though raw arithmetic > raw reading, the z scores reveal better relative performance in reading.

T-Score is developed by

Standard score system developed by W.A. McCall (1922, 1939)

Named in honor of E.L. Thorndike

Other Standard Scores

• Stanines

• IQ (Deviation IQ)

• SAT Scores (Linear Transformation Example)

IQ (Deviation IQ)

• Mean = 100, SD = 15 (typical)

• Approx. 95% of IQs fall between 70–130

• Another type of standard score

• Allows comparison across different age groups or tests

• Sometimes called deviation IQ

SAT Scores (Linear Transformation Example)

• Based on z scores

• Converted to scale with mean = 500, SD = 100

• Linear transformation: keeps direct relationship with raw scores

• Differences between raw scores = same differences between standard scores

Linear vs. Nonlinear Transformations

• Linear: Direct numerical relationship to raw score; differences preserved

• Nonlinear: Used when data aren’t normally distributed → creates normalized standard scores

Normalized Standard Scores

• Used when raw scores form a skewed distribution

• Process = "stretching" distribution into a normal curve shape

• Makes scores comparable across tests

• Caution: Should only be used if skewness is due to the test, not the population