Gas Laws and Stoichiometry Unit Set

law 1: particles in a gas will move..

in straight lines called translational motion until they collide elastically (with no energy or momentum lost) with other particles or sides of the container

law 2: temperature is a measure of..

the average kinetic energy (E_k = ½ mv²) of particles in a sample of matter

law 3: in an ideal gas, the volume of particles

is taken to be 0, they are modelled as a mathematical point.

law 4: in an ideal gas, there are..

no forces acting between particles, the kinetic energy of the particles overwhelms attraction, so attraction does not greatly affect particles

how do you increase kinetic energy?

add more kinetic energy or heat

what do the approximations of ideal gas laws break down?

these approximations will break down for real gasses at very low temperatures or at very high compression (pressure)

particles exert force on the sides of a container when they collide leading to this formula

pressure exerted by a gas = force / area or

newtons (N) / m² = Pascal (Pa)

P = k (1/v) or

PV = K

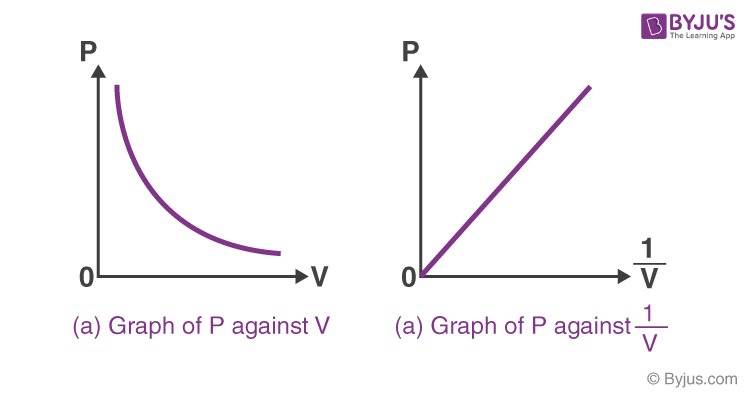
pressure is ________ proportional to

inversely proportional to volume of an ideal gas

increase in temperature (to V)

increase in collision frequency and collision energy, increase in volume

decrease temperature (to V)

decrease collision frequency and collision energy, decreased volume

temperature and volume have a

direct relationship at constant n/m and P

convert °C to K

add 273.15

convert K to °C

subtract 273.15

law of combining volumes (gay-lussac)

gasses react in specific whole number ratios by volume at constant T and P

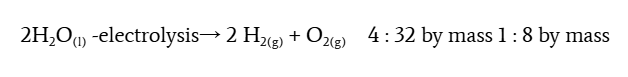
condition of volume ratio

ONLY for gasses, does not work for solids or liquid

definition of mV

We define Molar Volume as the volume of gas at a particular temperature and pressure consisting of one mole of gas

molar volume formula

mV = V/n

Density of an ideal gas

D_gas = mm/mV, this ONLY works for gasses

how to convert g/L to g/mL

divide by 1000 since the conversion is happening in the denominator

universal gas constant

R = 8.314 kPaL/Kmol (kilopascal litres/ Kelvin mol)

ideal gas law

R = PV / nT or PV = nRT

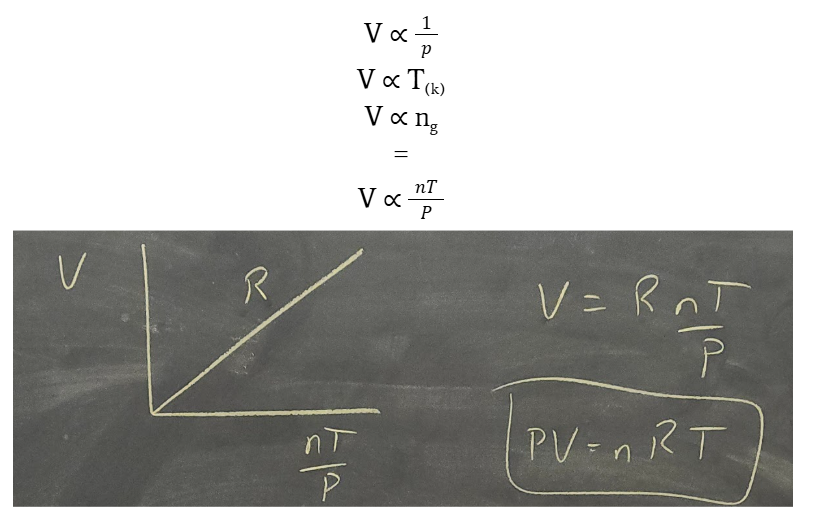
use ideal gas law to find molar volume

• PV = nRT

• V = nRT/P

• V/n = RT/P

• since V/n is molar volume, mV = RT / P

use ideal gas law to find density

• D = m/V

• V = m/D

• substitute V = m/D into PV = nRT

• Pm/d = nRT

• Pm = nRTD

• D = Pm/nRT

• since m/n is mm, D = mmP/RT

• since P/RT is mV, this is the same as D = mm/mV

use ideal gas law to find mm

• substitute n = m/mm into PV = nRT

• PV = mRT/mm

• mmPV = mRT

• mm = mRT/PV

boyle’s law

• Volume is inversely proportional to pressure at constant T and n

• P₁V₁ = P₂V₂

charles’ law

• volume is directly proportional to temperature in Kelvin at constant P and n (moles per mass)

• V₁/V₂ = T₁/T₂

Gay-Lussac’s law

• pressure is directly proportional to temperature in kelvin at constant V and n

• P₁/P₂ = V₁/V₂

combined gas law

P₁V₁/T₁ = P₂V₂/T₂ at constant n/m and T in kelvin

Avagadro’s law/hypothesis

• number of moles of gas is directly proportional to volume at constant T and P

• n₁/n₂ = V₁/V₂

Density of a gas

D_gas = mm/mV at specific T and P

Density

D = m/v

use ideal gas law to find density

• D = m/V

• V = m/D

• substitute V = m/D into PV = nRT

• Pm/d = nRT

• Pm = nRTD

• D = Pm/nRT

• since m/n is mm, D = mmP/RT

• since P/RT is mV, this is the same as D = mm/mV

use ideal gas law to find molar volume

• PV = nRT

• V = nRT/P

• V/n = RT/P

• since V/n is molar volume, mV = RT / P

use ideal gas law to find mm

• substitute n = m/mm into PV = nRT

• PV = mRT/mm

• mmPV = mRT

• mm = mRT/PV

standard conditions

• P_STP = 101.3 kPa

• T_STP = 0.00000 degrees C or 273.15 K

• mV_STP = 22.4 L/mol

Standard Ambient Temperature and Pressure

• P_SATP = 100.0 kPa

• T_SATP = 25.00 degrees C = 298.15 kPa

• mV_SATP = 24.8 L/mol

universal gas constant

R = 8.314 kPaL/Kmol