Chap 7A - Gaseous state

Compare

Volume

Shape

Compressibility

Density

Arrangement

Intermolecular forces

Vibration, rotation and translation

of solids, liquids and gas

	Solid	Liquid	Gas
Volume	Fixed	Fixed	Takes volume of container, greatly influenced by temperature and pressure
Shape	Fixed	Takes shape of container	Takes shape of container
Compressibility	0	0	High
Density	High	Moderate to high	Low, influenced by temperature and pressure
Arrangement	Particles are very close together, arranged in an orderly manner of long distance	Particles are close together, arranged in fairly orderly manner but there is no long range order	Particles are far apart, mainly empty spaces between particles
Intermolecular forces	Strong	Strong (not as strong as solids)	Very weak
Vibration, rotation and translation	Particles vibrate and rotate about fixed positions but are not free to move throughout solid	Particles vibrate, rotate and move throughout the liquid	Particles move very freely throughout container

State assumptions of an ideal gas

1. Gas particles are of negligible size and volume compared to volume of container 

2. Gas particles have negligible intermolecular forces of attraction 

3. Collisions between gas particles are perfectly elastic (gas particles bounce apart with no loss in kinetic energy on collision) 

4. Gas particles are in continuous, rapid, random and linear motion 

5. Average kinetic energy of gas particles is proportional to temperature on the kelvin scale

State and explain conditions for ideal gasses

1. At low pressures

• The gaseous molecules  relatively far apart + volume of the molecules themselves is negligible compared to the volume of the container -> real gas molecules at low pressure can be approximated to have negligible volume

• Also, intermolecular forces are negligible as the particles are far apart -> their behaviour at low pressures would approach that of ideal gases

2. At high temperatures

• Gas particles have enough kinetic energy to overcome intermolecular forces, which can thus be considered insignificant

• As such, the behavior of real gases approach ideal gas behavior at high temperatures

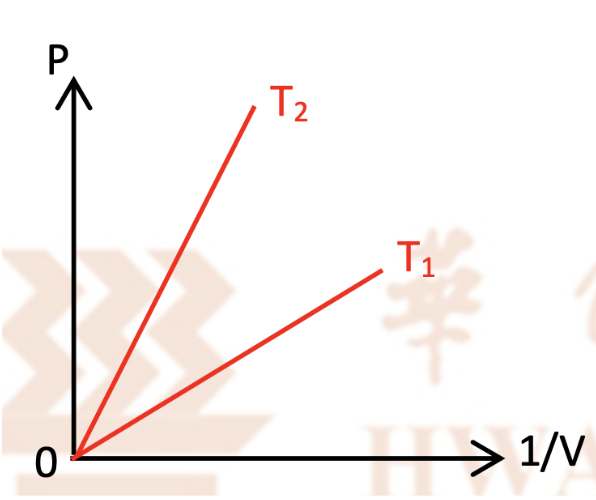
 Which temperature is higher , T1 or T2? Explain

Rearrange PV = nRT and make P the subject of the equation, we will get P = (nRT)(1/V) Therefore, plotting P against 1/V will give us a straight line that passes through the origin with gradient = nRT Since the graph with T2 is a steeper line than that of T1, that means nRT2 > nRT1. This is only possible if T2 > T1. Hence T2 has a higher temperature than T1

State properties of real gasses

1. Gas particles have significant volume compared to volume of the container 

2. There are significant intermolecular forces of attraction between gas particles 

State the conditions when gases would deviate from ideal conditions

• Real gases would deviate from ideal behavior at high pressures and low temperatures as they are most likely to condense into a liquid -> behave ideally at high temperatures and low pressure 

• They do not obey ideal gas equation at very high pressures and very low temperatures as they are most likely to condense 

  • Liquefaction is a key property of real gases that is not predicted by the kinetic theory of gases, as it requires the action of intermolecular forces (which the theory assumes to be negligible) in order to occur -> ideal gases never condense into liquids

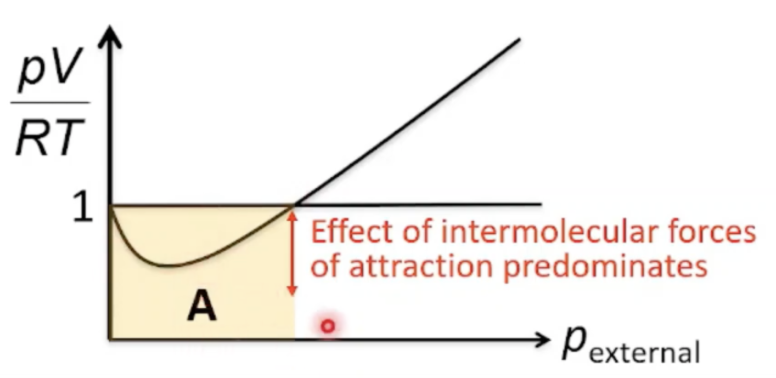
Explain pV value at moderately high pressure

• At first blue bracket of graph, there is negative deviation (pressures up to 400atm), values of pV/RT are lower than ideal (< 1) due to significant intermolecular forces of attraction 

• Molecules that are about to strike the walls of the container experience intermolecular forces of attraction -> attractive forces decrease force of collisions between molecules and walls -> impact on walls reduced -> pressure exerted less than expected Pobserved < Pideal -> pV smaller than ideal value

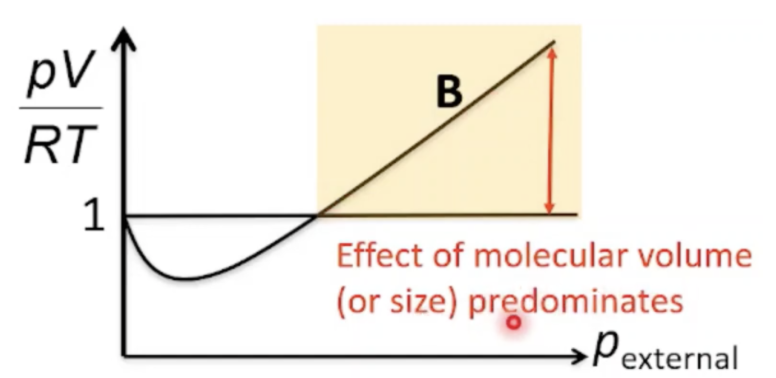
Explain pV value at very high pressure

• At 2nd blue bracket of graph, there is positive deviation where values of pV/RT are greater than ideal (> 1) 

• At high pressures, the volume of the container decreases

• The molecules are pushed closely together and take up a significant portion of the container volume, resulting in less space in which the molecules can move

• Particles occupy a significant volume compared to the container volume

• Gas is less compressible and volume of gas observed is greater than ideal volume in which molecules are move about -> pV higher than ideal value 

• Since the gas particles are close together, they tend to interact with one another, hence intermolecular attractions are not negligible

Explain how real gases deviate from ideal behaviour at low temp

• As temperature is lowered, the kinetic energy of the gas particles decreases, causing them to move more slowly and intermolecular forces to become more significant

• This also causes collisions to become inelastic (such that assumption 3 is no longer valid either) -> it reaches a point where the particles can no longer overcome the intermolecular forces, causing: 

  • A molecule striking the wall of container experiences a force of attraction from other molecules and is pulled back -> lesson impact of wall -> pressure less than ideal OR 

  • Real gases liquefy (condense to form a liquid) when cooled to below its boiling point

Describe the other effects causing real gasses to deviate from ideal conditions

1. At very high pressures where effect of molecular size or volume predominates, larger molecules experience greater deviation

2. At moderately high pressure where intermolecular forces of attraction predominates, molecules with stronger intermolecular forces have greater deviation 

• Eg. CO2 has a larger electron cloud and hence stronger dispersion forces than N2, hence CO2 deviates more from ideal behaviour.

  • For molecules with similar electron cloud size, other intermolecular forces besides dispersion forces need to be considered. NH3, with stronger hydrogen bonding, should deviate more from ideal behaviour than CH4, with only intermolecular dispersion forces

3. The H2 and H2 curves do not show the typical dip at moderate pressures

• The IMF are so weak that the effect caused by molecular size or volume predominates at all pressures

State the type of molecules that deviate the most

Molecules that deviate the most: 

1. Polar gases due to strong pd-pd or hydrogen bonds 

• Polar molecules (Eg. NH3) with hydrogen bonding deviate more than those with id-id (Eg. N2)

2. Large and heavy molecules due to significant molecular size or volume