FORMULAS

solving quadratic equations by EXTRACTING SQUARE ROOT

written as x² = k (k is the given value)

if k > 0

1. get square roots of x and k

2. find two possible values for x (±)

if k = 0

1. set k’s value to 0

   (no real solution)

if k < 0

1. leave the problem be since it has no real solution or root

solving quadratic equations by FACTORING

written in standard from and either as a binomial (ax² + bx) or trinomial (ax² + bx + x)

factoring trinomials (when a = 1)

1. write the given in standard form (ax² + bx + c)

2. find two numbers that have a product of c, and have a sum of b

3. find the two possible values for x

factoring trinomials (when a > 1)

1. write the given in standard form (ax² + bx + c)

2. multiply a and c. the product given here will serve as the new value of c

3. find two numbers that have a product of c, and have a sum of b

4. divide each by the ORIGINAL COEFFICIENT OF A (the one before multiplying it with c)

5. find the two possible values of x

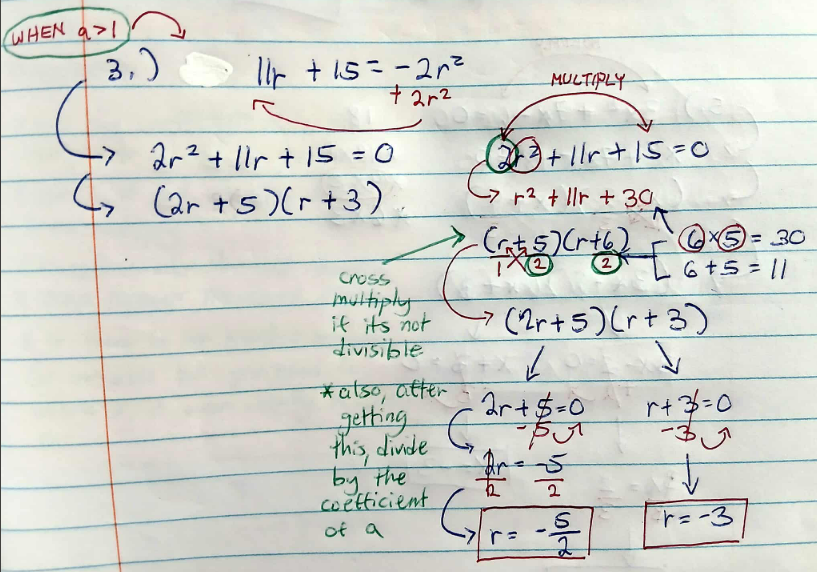
solving quadratic equations by completing the square

shown if a, b, or c is missing in the equation OR if the equation isn’t a perfect square trinomial

if A or C is missing

1. get the square root of either A or C (depends on what you have there)

2. divide B by 2 (always 2)

3. get the root of A/C from earlier, and divide the quotient of B by it

4. square the quotient of B and A/C

when B is missing

1. get the square root of A and C

2. multiply both roots of A and C together

3. multiply the product of A root and C root by 2 (always 2)

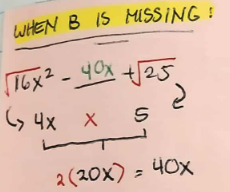
when it isnt a perfect square trinomial

1. write the given in this form: (ax² + bx = c)

2. divide A, B, and C by the coefficient/number of the quadratic term (a)

3. focus on the coefficient of B. divide it by 2, then square it.

4. with the new number we got, add it to both sides (beside B and C)

5. simplify the equation by combining like terms and factoring the trinomial

6. find the square root of C

7. solve for two possible values of x

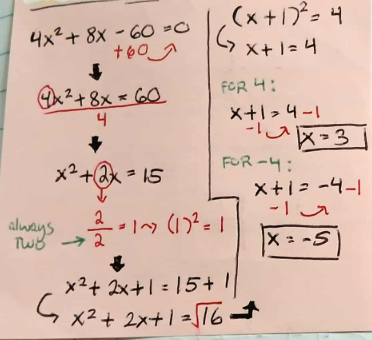
quadratic formula

1. write the given in standard form (ax² + bx + c = 0)

2. get the values of A, B and C

3. replace A, B, and C in the quadratic formula with the values you have

4. PEMDAS (parenthesis, exponents, multiplication, division, addition, subtraction)

5. solve for the two possible values of x

   (take note that in the quadratic formula, the “-” in -b doesn’t change. it means -1(b))