Ch. 10: Oscillations

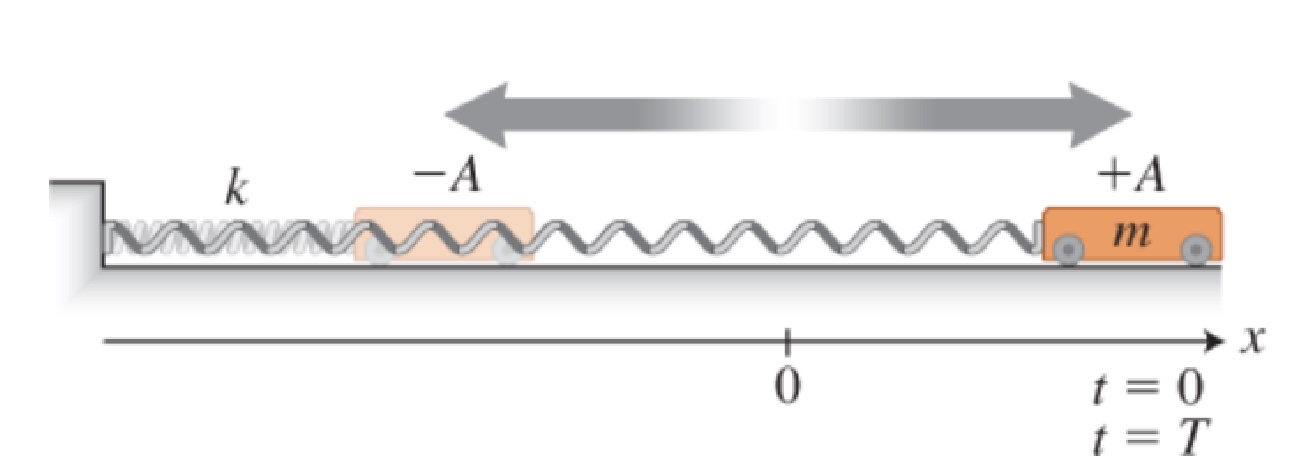
Vibrational motion

-the repetitive movement of an object back and forth about an equilibrium position

*motion that repeats in some known manner

-Examples: pendulum, spring

equilibrium position

x=0

*-A to +A= one complete oscillation

-T

-f

-A

-k

-m

-T= period of oscillation in seconds = time for motion to repeat once (1 full cycle) = 1/f

-f= frequency of oscillation in Hertz or Hz = 1/second (inverse period)

-A= amplitude = maximum displacement from equilibrium (a distance, + or -)

-k= effective spring constant in N/m (how stiff the spring is; larger = harder to stretch or compress/more stiff)

-m= mass attached to spring in kilograms (kg)

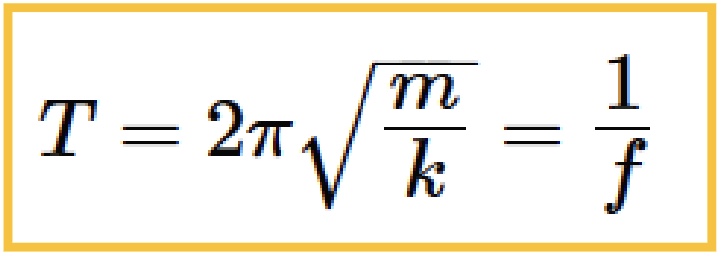
Hooke’s Law

-the resorting force/spring is directly proportional to the compression or extension of the system

*won’t have to use, but understand bc relates to spring constant; as spring constant goes up, the restoring force also goes up

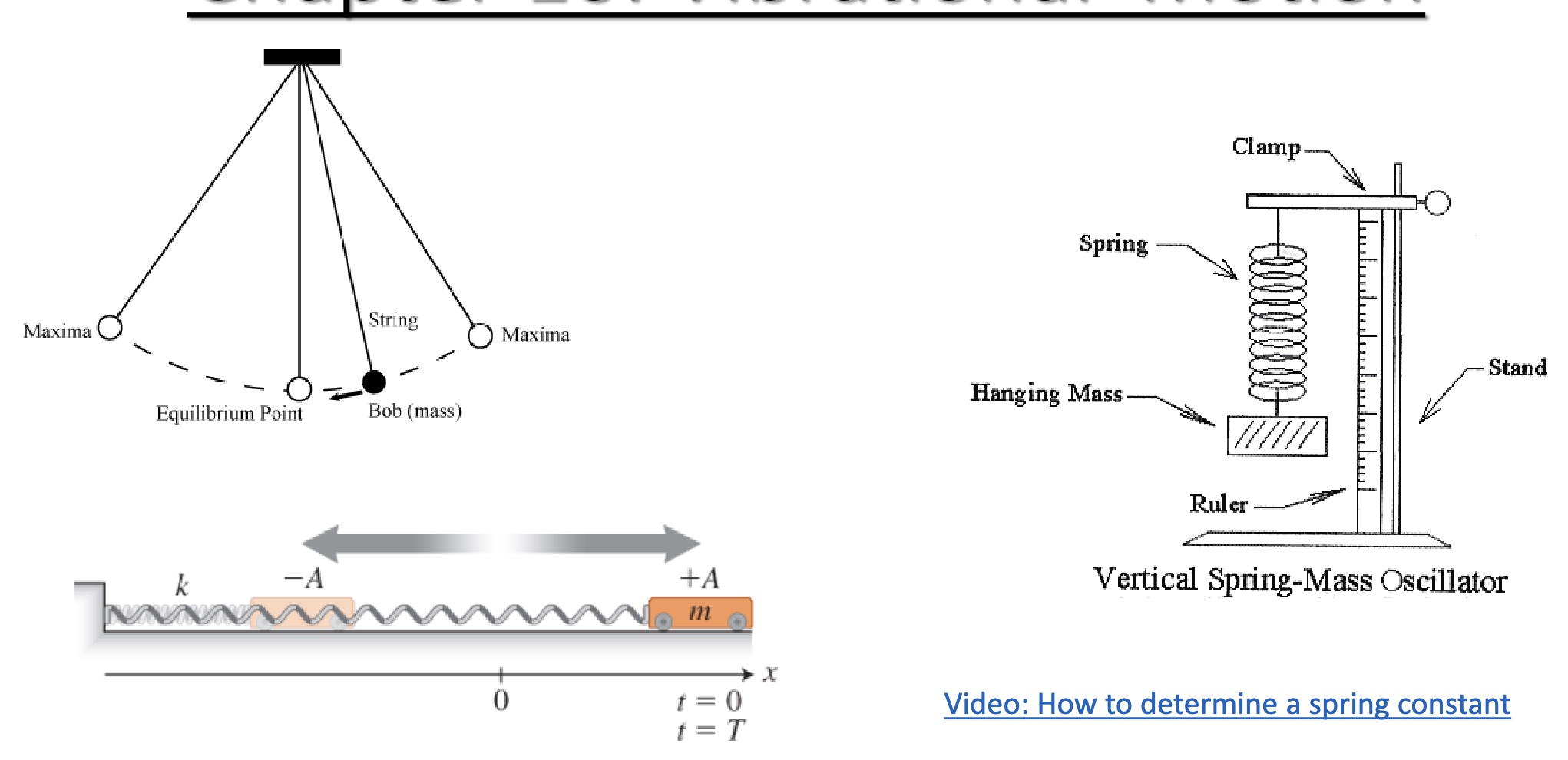
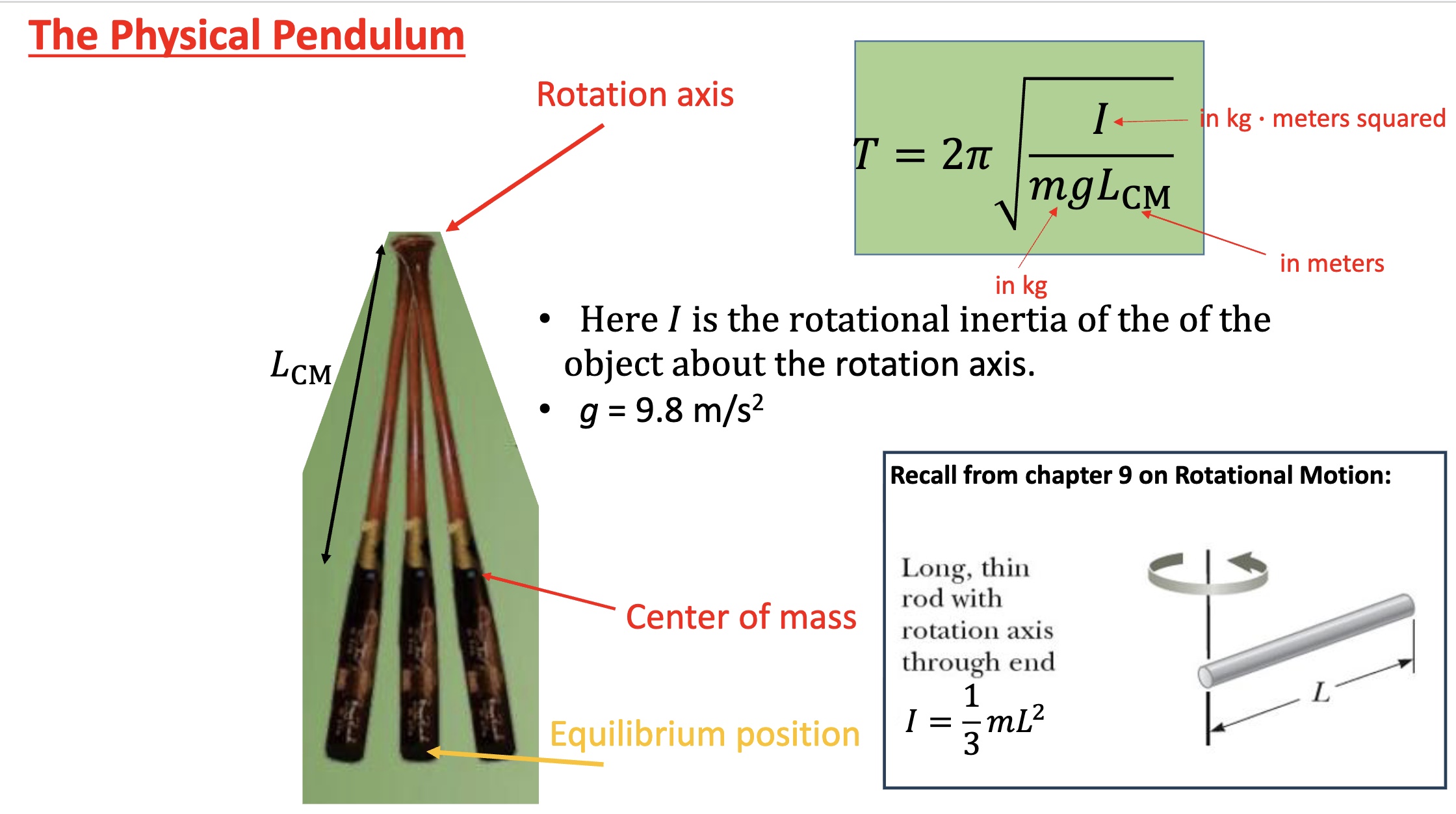
The Physical Pendulum

-any object swinging back and forth

-has a rotation axis, center of mass, and equilibrium position (when vertical)

-I (rotational inertia) for a long rod= 1/3mL²

-”Lcm”= length (in meters) from the rotation axis to the center of mass

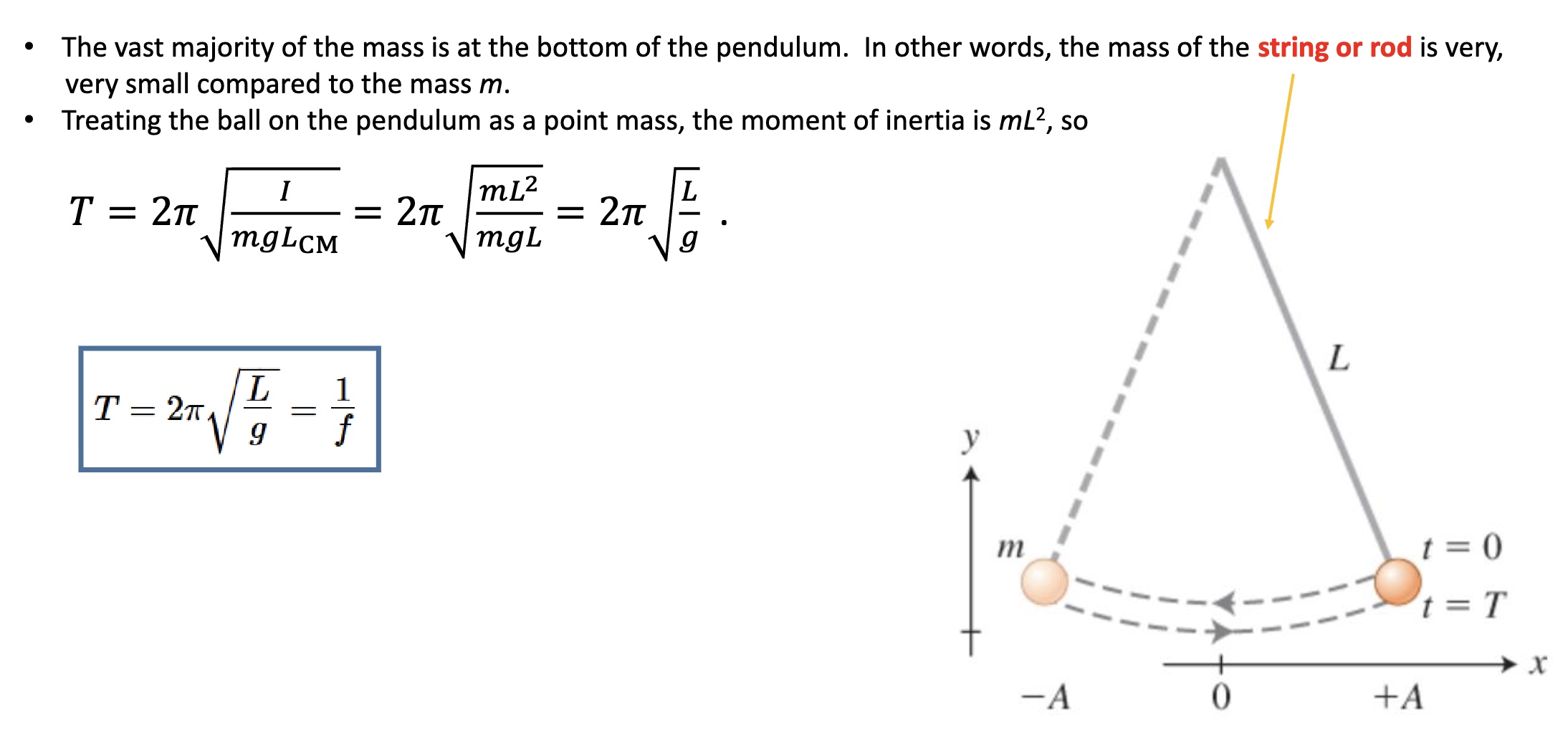
The Simple Pendulum System

-the vast majority of the mass is at the bottom of the pendulum. The mass of the string or rod is very small compared to the mass m

-Treat the ball on the pendulum as a point mass, so the moment of inertia is mL²

*thus, the period only depends on length and gravity! (not mass or amplitude/how far it gets pulled back)

*L=entire length of the pendulum

Simple Harmonic Motion

-a mathematical model of vibrational motion when position x, velocity Vx, and acceleration ax of the vibrating object change as sine or cosine functions with time

*”simple”=friction not important, “harmonic”=repeating

-applies to a spring (horizontal or vertical) with a mass or a pendulum

*t= time elapse since t=0

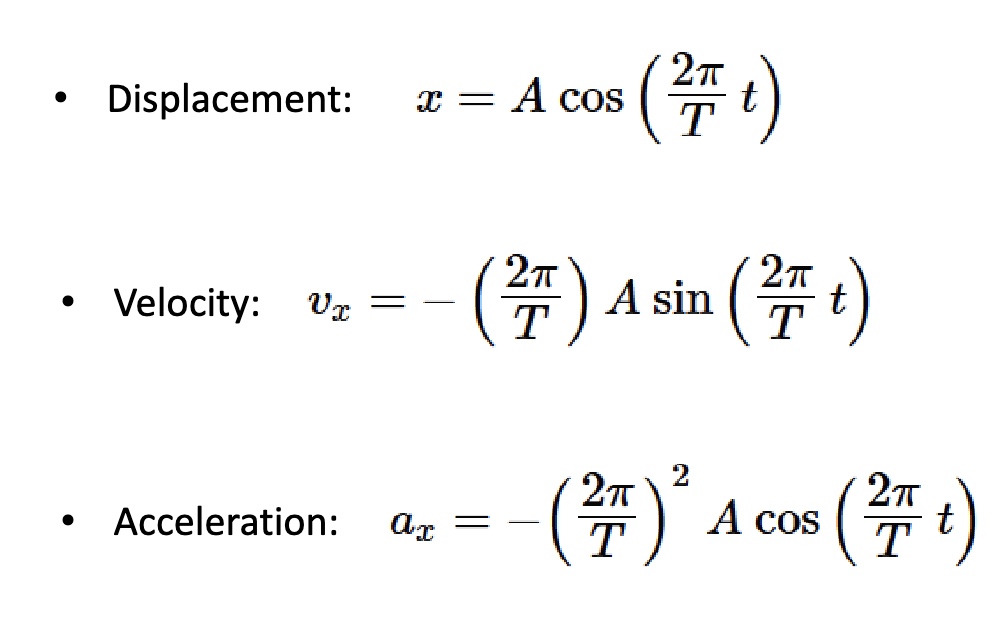
for simple harmonic motion calculations (displacement, velocity, and acceleration), make sure to put your calculator in….

radian mode!!!

at x=+A…

*motion starts at x=+A

-t=0

-Vx=-(2π)/Tsin(0)=0

-ax= -(2π/T)²Acos(0)=-(2π/T)²A

• max acceleration down

*negative=down (bc FNext down)

at x=0…

-t=T/4

-Vx=-(2π/T)Asin(2π/T * T/4) =-(2π/T)A

• max velocity

-ax=-(2π/T)²Acos(2π/T * T/4) = 0

*because force of the spring = force of gravity (acceleration increase to equilibrium and decreases once pass)

where are max acceleration up and down? when is acceleration zero?

-max acceleration down is at x=+A

*ax=-(2π/T)²A

-max acceleration up is at x=-A

*ax=+(2π/T)²A

-zero acceleration when x=0

*bc Fsp=Fg or FNet=0

where are max velocity up and down?

-max velocity down is at x=0

*Vx=-(2π/T)A

-max velocity up is at x=0

*Vx=+(2π/T)A

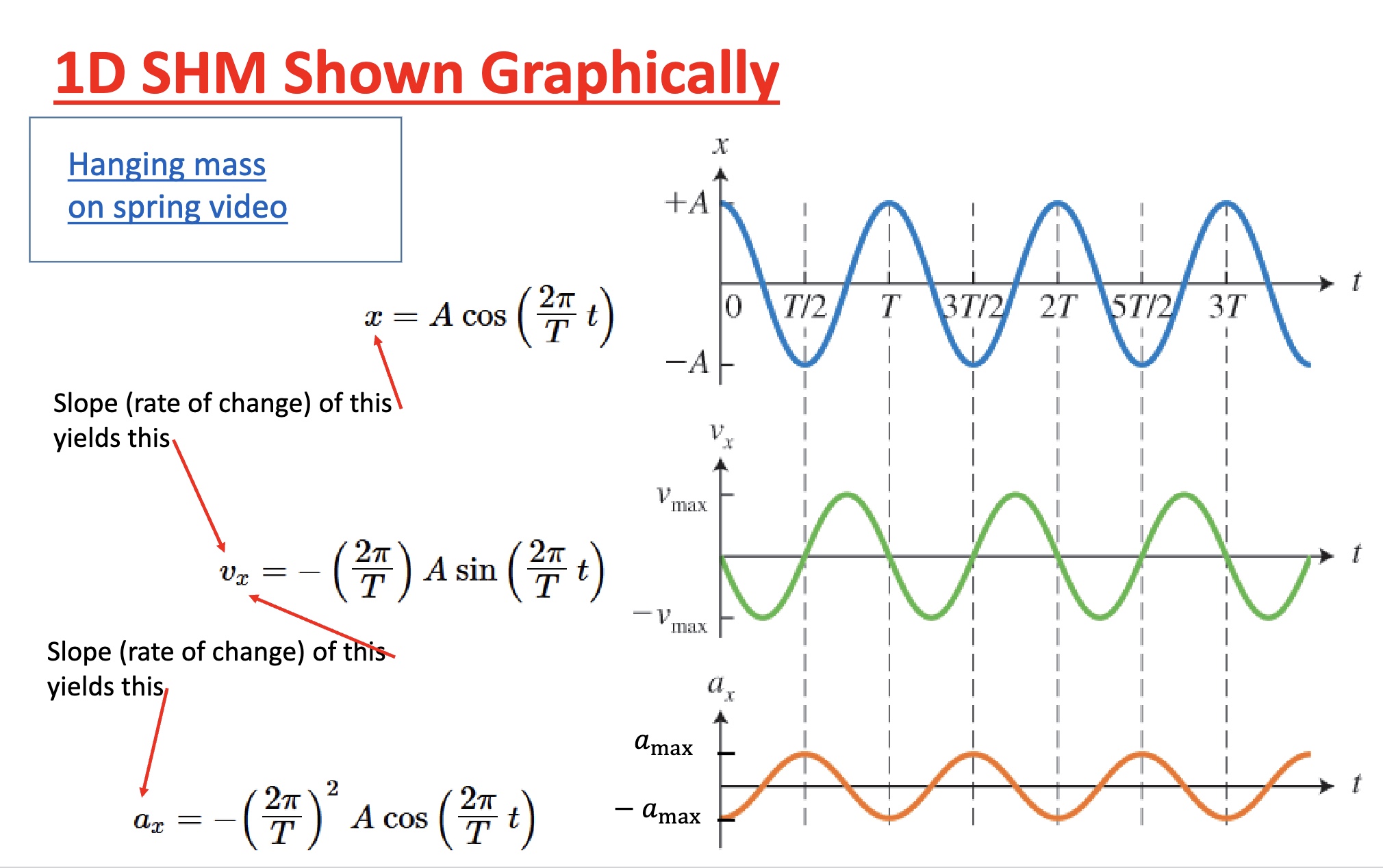
1D SHM shown graphically

-from PHYS 1001: slope of one graph gives you the next graph (ex: slope of the position versus time graphs gives you the velocity vs time graph, and similar with velocity vs time and acceleration vs time)

*ask yourself if the slope if positive, negative, or zero

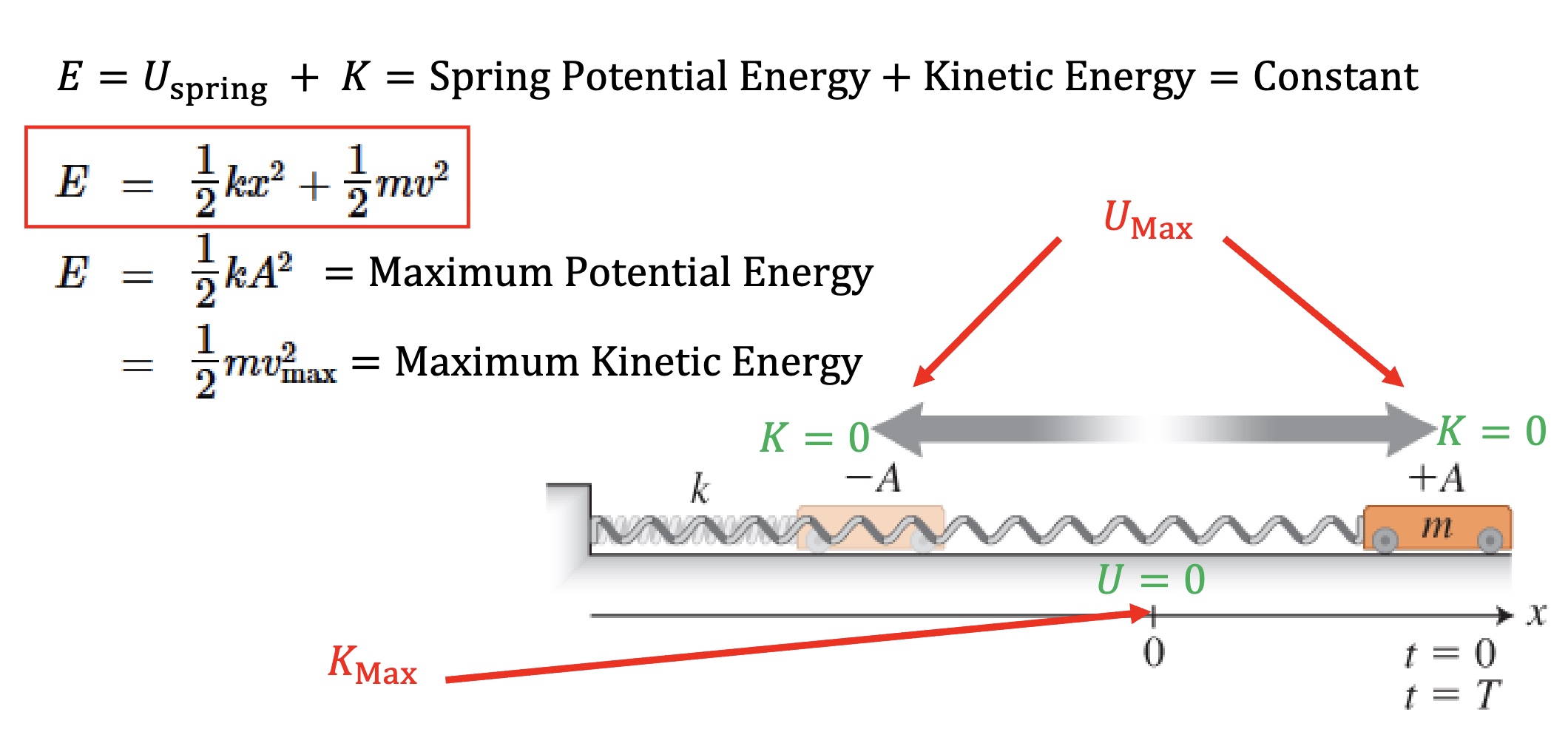
The total mechanical energy of a spring-object system vibrating horizontally

-E (total mechanical energy, in Joules) is always constant

-at equilibrium (x=0): only have kinetic energy, and where have max velocity

• in the equation: k=spring constant; x=how much the spring is compressed or stretched (displacement from equilibrium)

-at -A and +A: only potential energy (no KE or velocity)

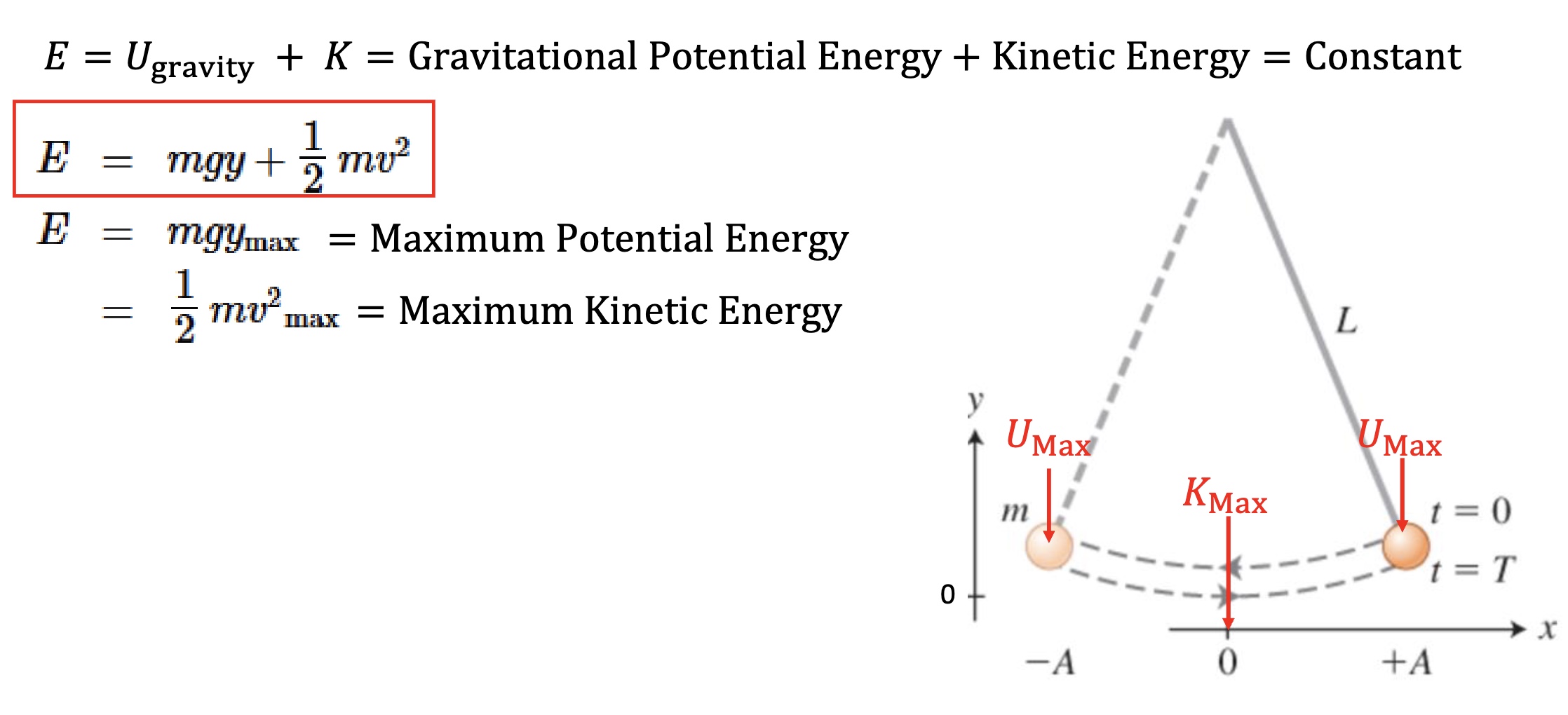
The total mechanical energy of a simple pendulum-Earth system

-E (total mechanical energy, in Joules) is always constant

-Remember GPE changes w/ height, choose y=0 when pendulum is completely vertical (y=how high above or below zero)

-at y=0: no GPE, but have max velocity so max KE

-at -A or +A: max GPE, no velocity (pendulum stops moving), and max height (so ymax)