Calc 3 Test 1 Things to Remember

Circular Cylinder

x² + y² = c

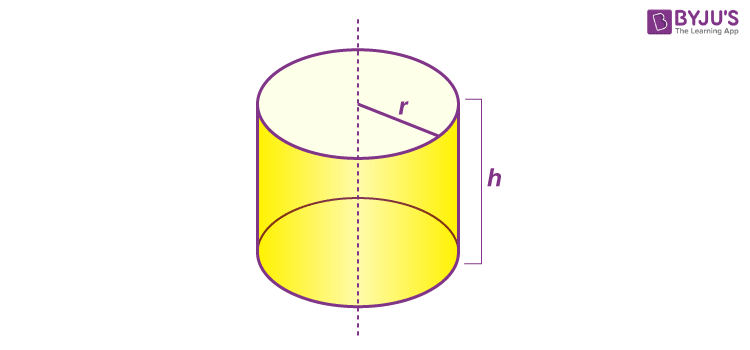
Parabola

z = c - y²

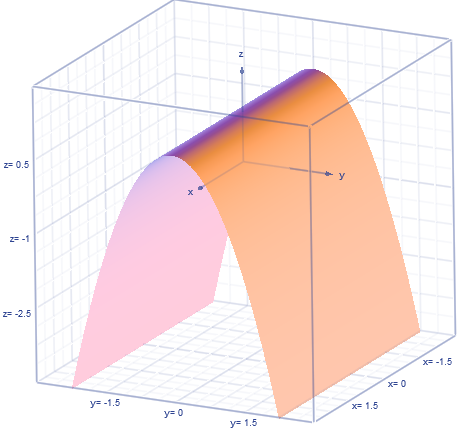
Ellipsoid

x²/a² + y²/b² + z²/c² = k

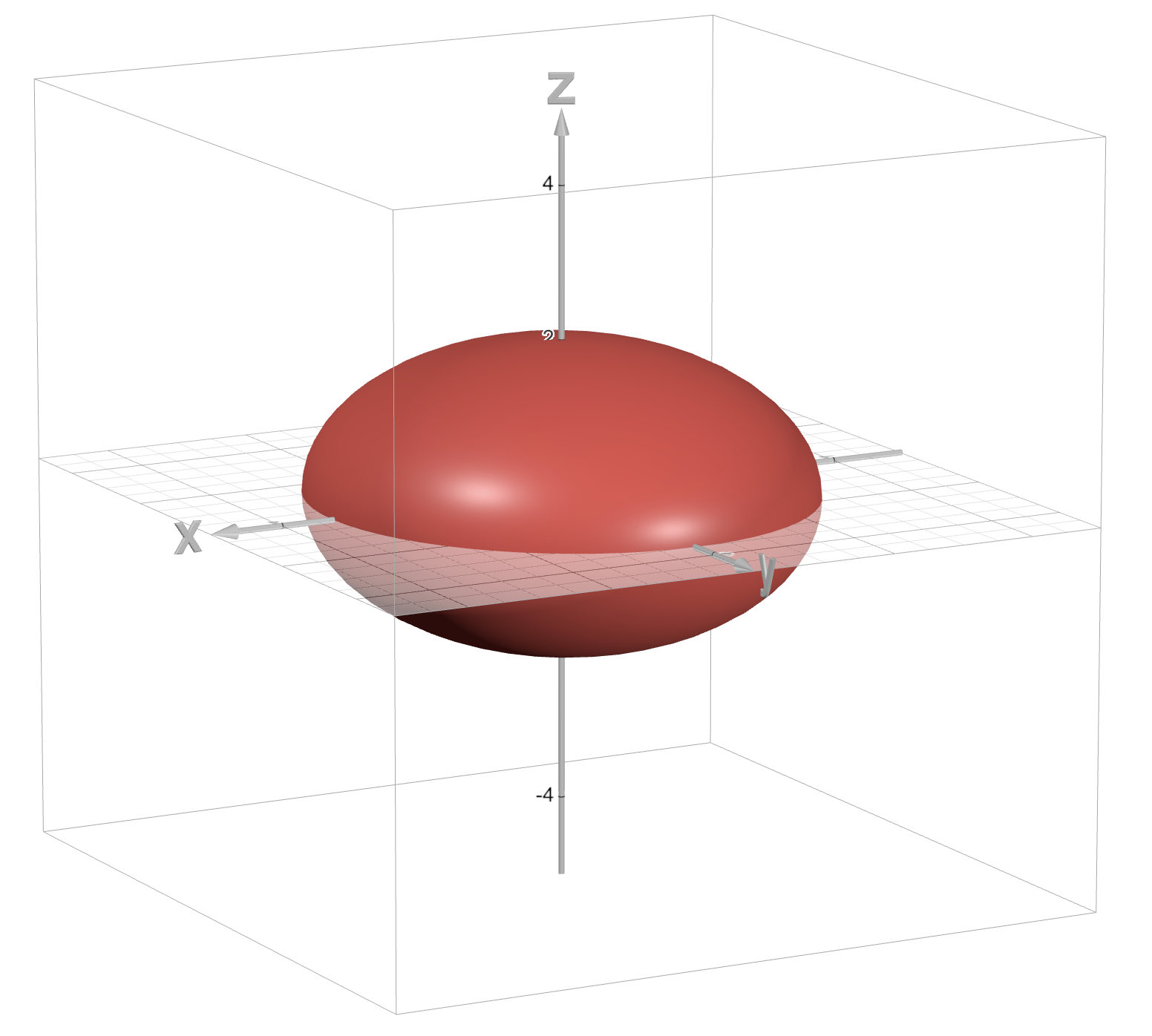
Hyperbolic Cylinder

x²/a² + y²/b² = -1

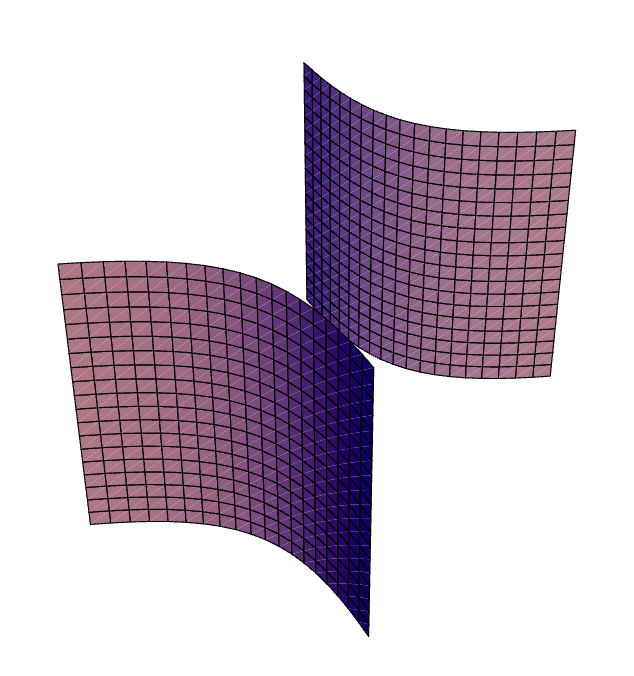
One Sheeted Hyperboloid

x² + y² - z² = 1

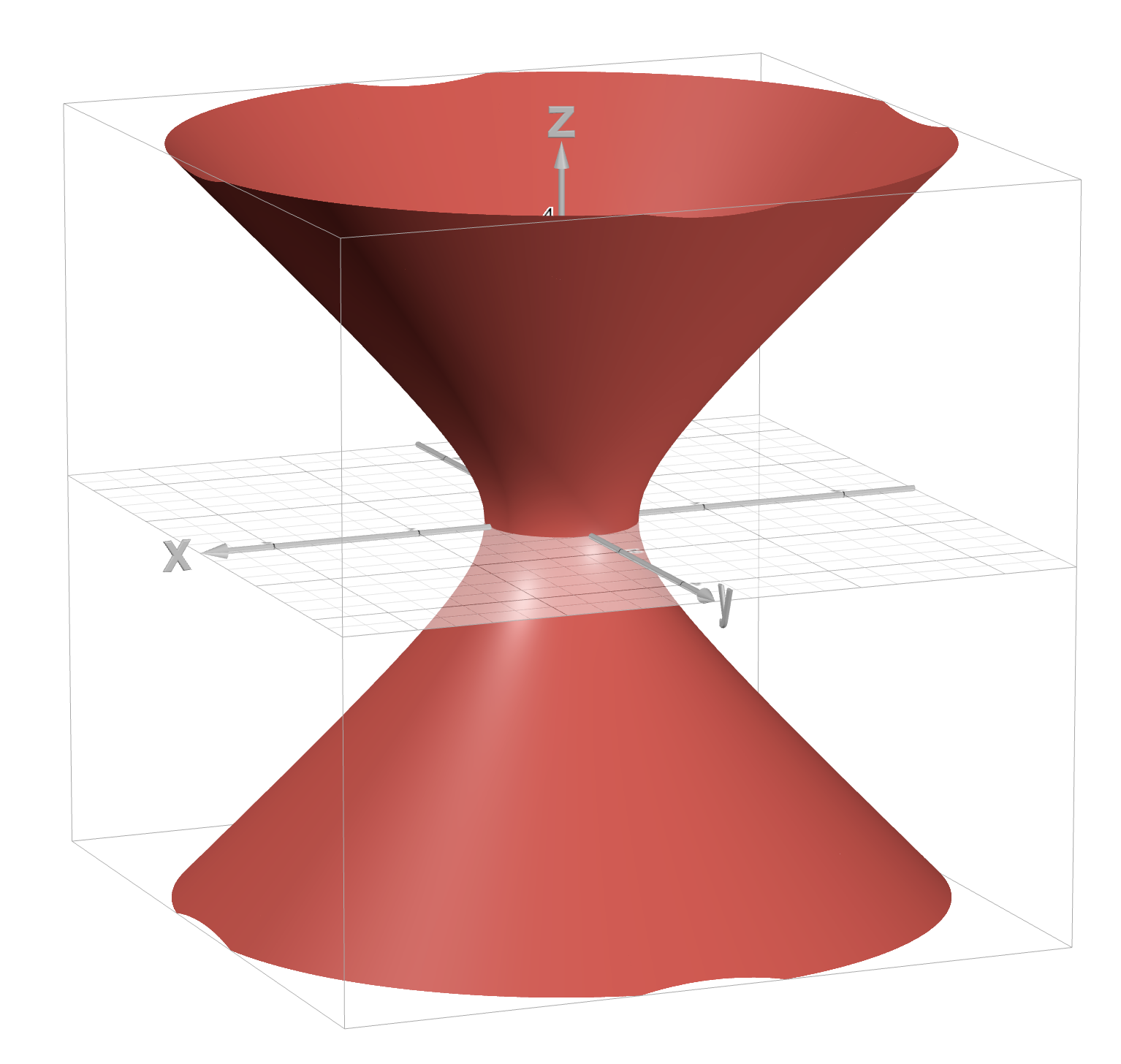
Two Sheeted Hyperboloid

z² - x² - y² = 1

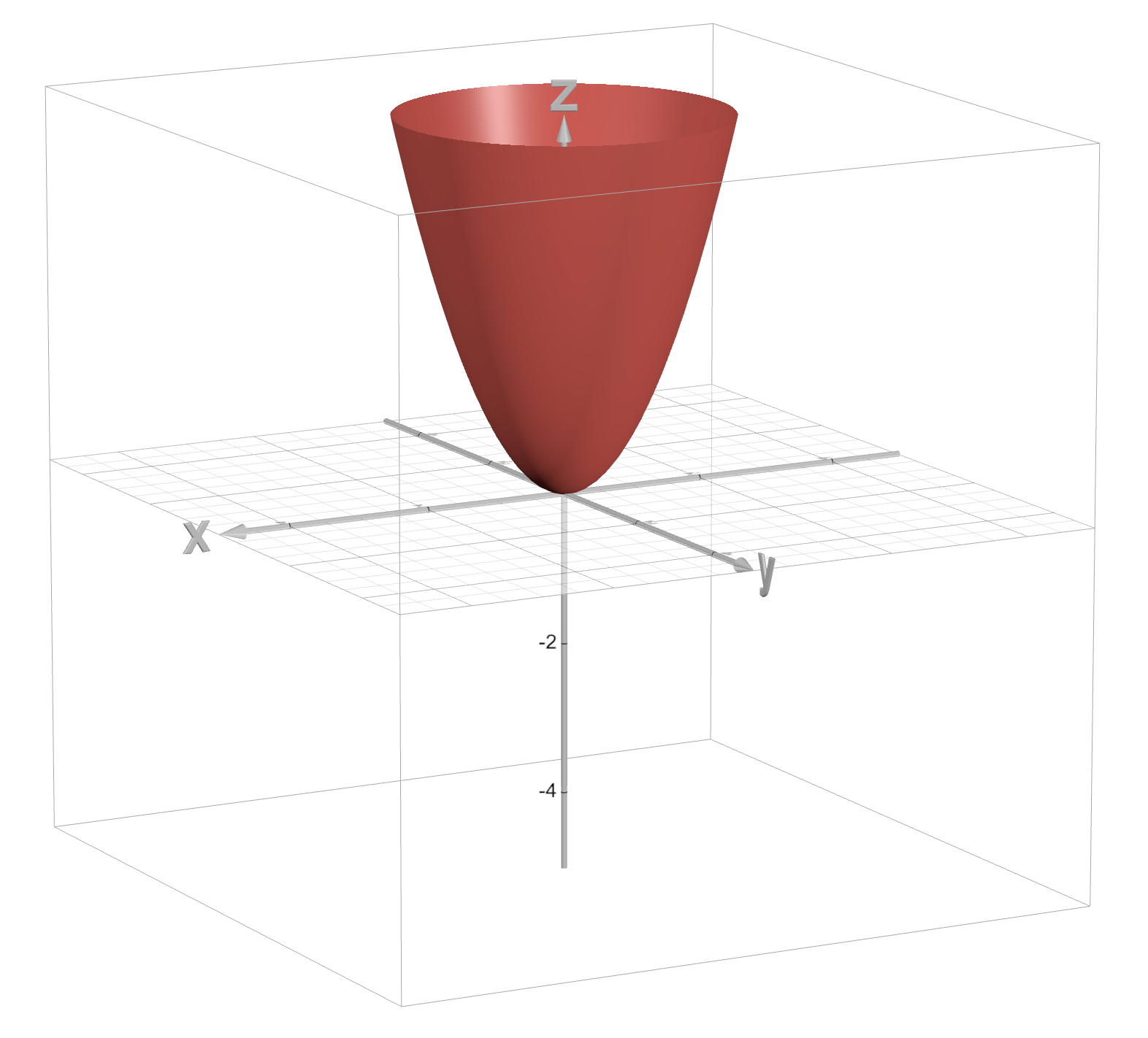
Elliptic Parabaloid

z = x² + y²

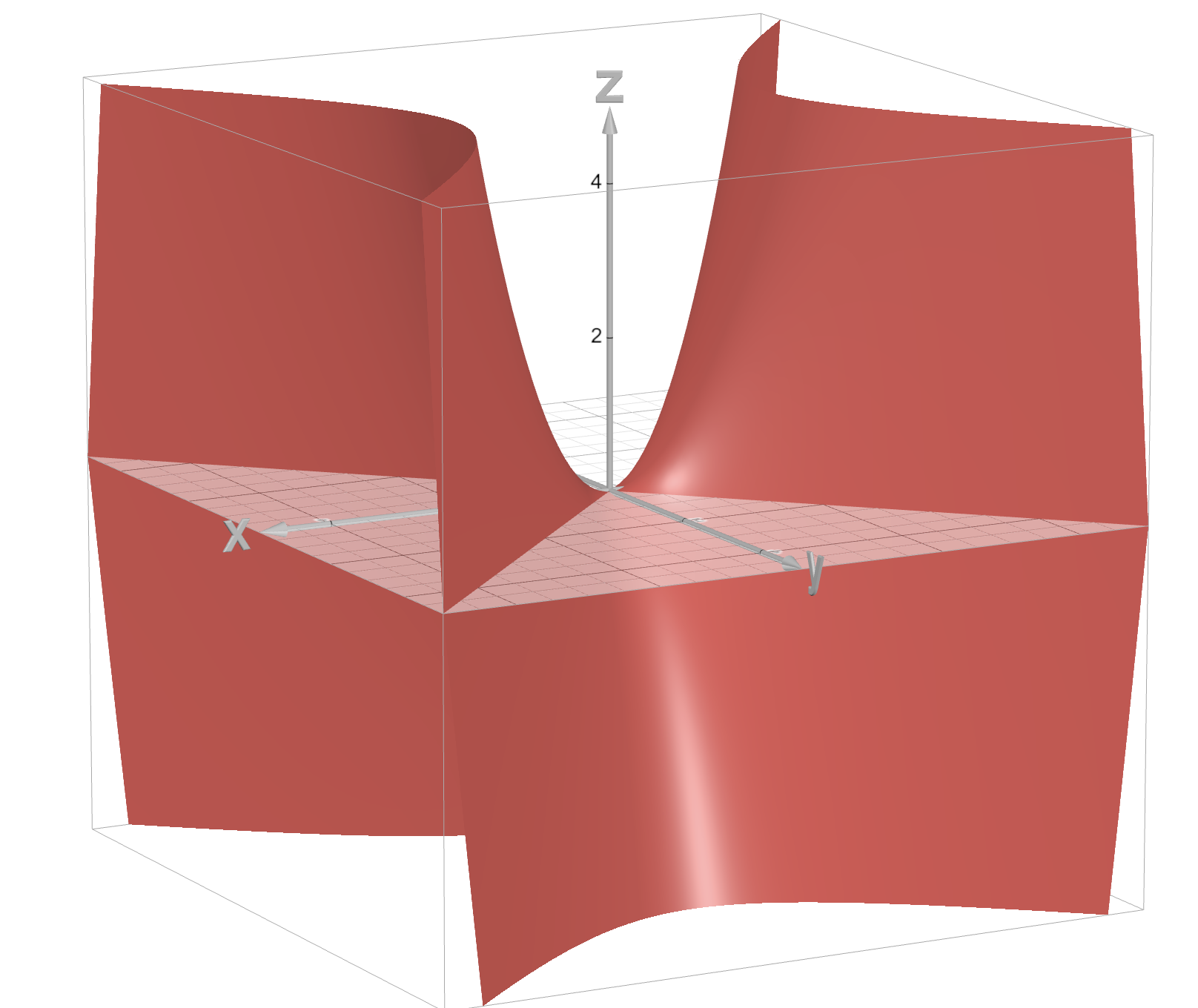
Hyperbolic Parabaloid

z = x² - y² (“saddle”)

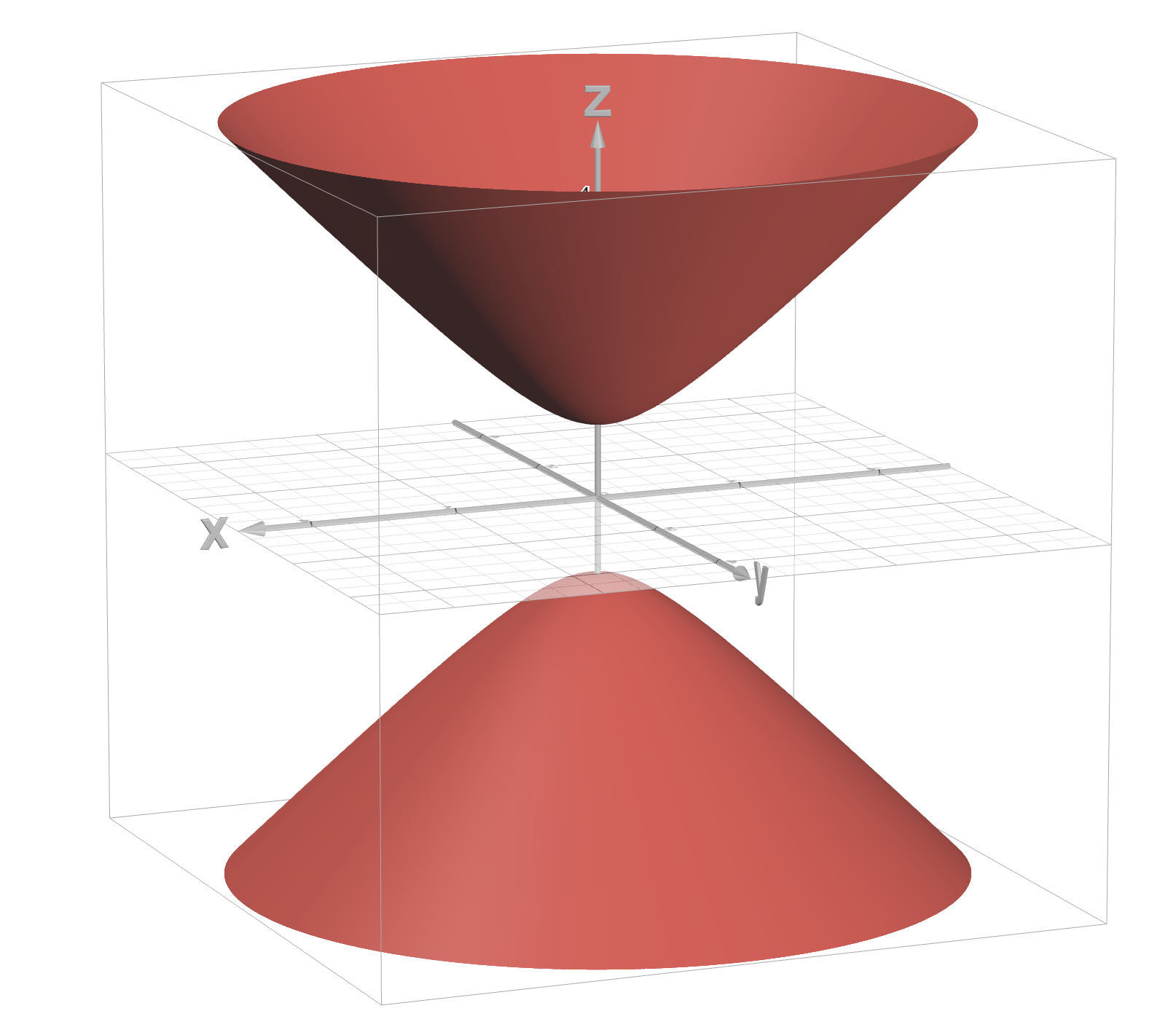
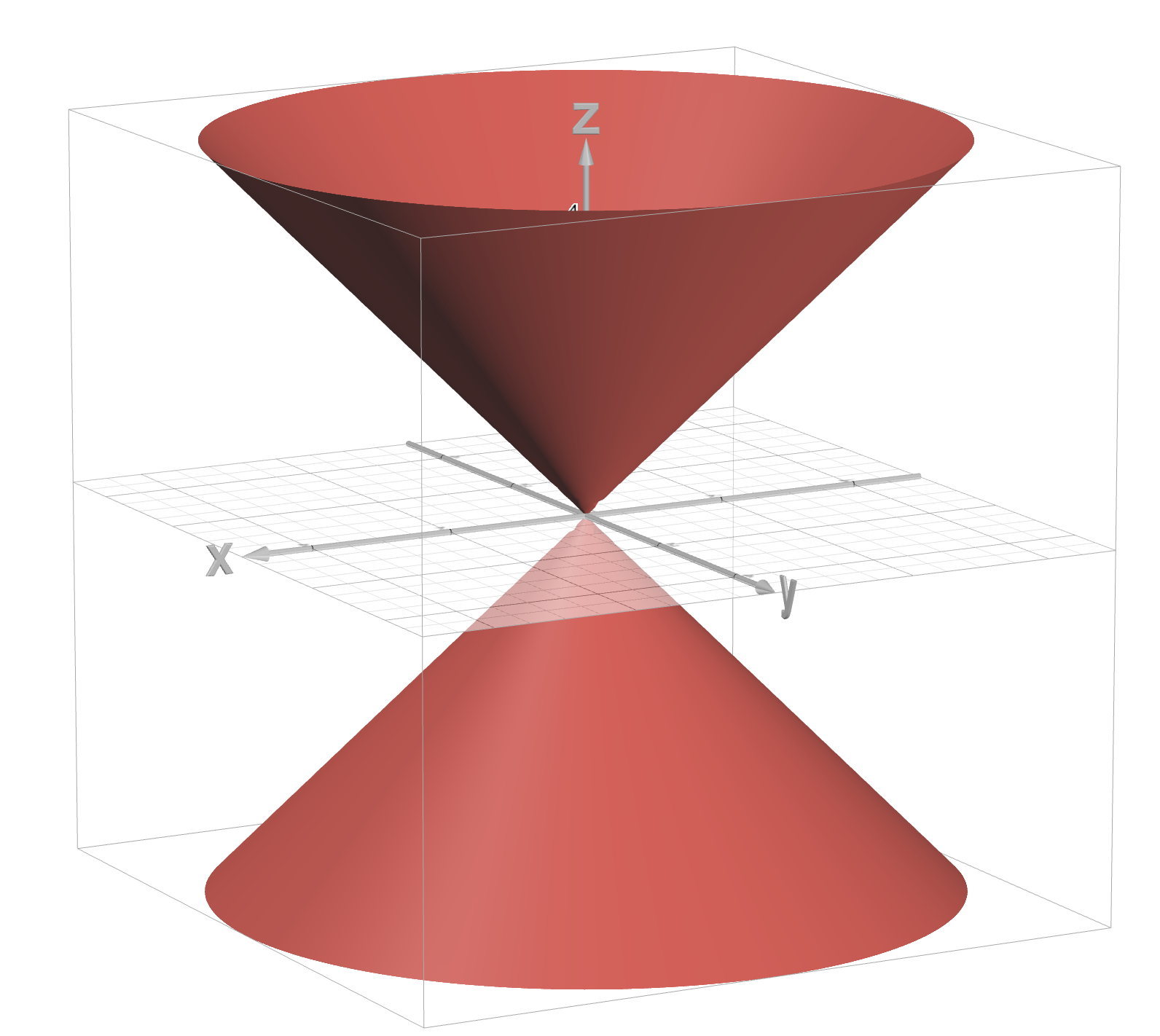
Cone

z² = x² + y²

dy/dx for a parametric curve <x(t),y(t)>

dy/dt ÷ dx/dt

d²y/dx² for a parametric curve <x(t),y(t)>

d/dt(dy/dx) ÷ dx/dt

integral from a to b of a parametric curve <x(t),y(t)>

integral from ta to tb of [y(t)x’(t)dt]

arclength for a parametric curve <x(t),y(t)>

integral from ta to tb of sqrt(x’(t)²+y’(t)²)

(dot product) a•b = ….

|a||b|cosθ

Unit tangent vector T(t)

r’(t)/|r’(t)|

Unit normal vector N(t)

T’(t)/|T’(t)|

Unit binormal vector B(t)

T x N

scalar projection of b onto a

(a • b)/|a|

vector projection of b onto a

(a • b)/|a| * a/|a|

sin2t (double angle identity)

2sintcost

cos2t (double angle identites)

2cos²tsin²t, 1 - 2sin²t, 2cos²t - 1

sin(x ± y)

sin(x)cos(y) ± cos(x)sin(y)

cos(x ± y)

cos(x)cos(y) ± sin(x)sin(y)

equation for a plane (given normal vector <a,b,c> and point (x0,y0,z0))

a(x−x0)+b(y−y0)+c(z−z0)=0

area of parallelogram formed by two vectors (double area of the triangle)

|PQ x PR|

|AxB| =

|A||B|sinx

direction vector for line of intersection between two planes

a = n1 x n2

Formula for distance from a point to the plane

D = (ax₁ + by₁ + cz₁)/sqrt(a²+b²+c²)