States of Matter Weeks 7-12 ILOs and Concepts

Describe the variables of state.

Variables of state are the variables needed to specify the state of a system. They include:

• amount of a substance it contains, n

• volume it occupies, V

• pressure, p

• temperature, T

Explain how the partial pressures or gases in a mixture relate to total pressure.

Total pressure = sum of partial pressures of each component

P = p_a + p_b + p_c + …

Rationalise how pressure changes as a result of changing the number or speed of molecules.

Pressure increases if number or speed of molecules increases as more collisions with the container walls and each other occur.

Work

Done in order to achieve motion against an opposing force

Kinetic energy

Energy as a result of motion

Potential energy

Energy as a result of its position

Total energy

Sum of kinetic energy and potential energy

Coulomb potential energy

Energy between 2 charges separated by a distance r. Varies as 1/r

Boltzmann distribution

Formula for calculating the relative positions of states of various energies

Boyle’s law

p inversely proportional to V

Charles’ Law

V proportional to T

p proportional to T

Avogadro’s principle

V proportional to n

Physical state

Its form (soild, liquid or gas) under the current conditions of pressure, volume and temperature

Equation of state

An equation that interrelates the variables that define the state of a substance

Perfect gas

Gas that obeys the perfect gas law under all conditions

Describe the assumptions used in the kinetic model

• molecules of a gas behave identically

• molecules are hard, perfectly elastic spheres

• volume of molecules negligible compared to the volume of the container

• no intermolecular forces between the molecules

• molecules move in continuous random motion

Explain the features of the Maxwell-Boltzmann distribution of speeds

y axis: percentage/proportion of particles, x axis = energy

highest point is where most of the particles are found

higher temperatures - curve moves right and down

Describe how molecules behave in perfect and real gases

In perfect gases, molecules behave with no intermolecular forces whereas real gases have intermolecular forces and the volume of real gases is no longer negligible as it is in perfect gases. Real gases deviate from perfect gases at high pressures and low temperatures.

Interpret experimental isotherms and use them to identify the values of critical constants

Experimental isotherms plot pressure against molar volume at different temperatures. They usually show that at small molar volumes gases deviate more from the perfect gas isotherm

Kinetic model of a gas

Considers only the contribution to the energy from the kinetic energies of the model and accounts for the equation of state of a perfect gas

Maxwell-Boltzmann distribution of speeds

Gives the fraction of molecules that have speeds in a specified range

Collision frequency

Average number of collisions made by a molecule in a period of time divided by the length of that period

Mean free path

Average distance a molecule travels between collisions

Compression factor

Helps summarise the extent of deviations from perfect behaviour

compression factor = measured volume (molar volume)/calculated volume of a perfect gas

Virial equation

Empirical extension of the perfect gas equation that summarises the behaviour of real gases over a range of conditions

Critical temperature

Gas can be liquefied by pressure alone if temperature is at or below the critical temperature

Van de Waals equation

Model equation of state for a real gas

Interpret and describe the features of phase diagrams

T₃ is the triple point where solid, liquid and gas all exist in equilibrium and is at a specific temperature and pressure for each substances. The triple point is also the lowest pressure at which the liquid phase of a substance can exist.

T_c is the critical point where the interface/boundary between liquid and vapour disappears and a single, uniform phase called a supercritical fluid is left.

Phase transition

Spontaneous conversion of one phase into another

Phase

Form of matter that is uniform throughout in chemical composition and physical state

Phase diagram

Indicates the values of pressure and temperature at which a particular phase is most stable or is in equilibrium with other phases

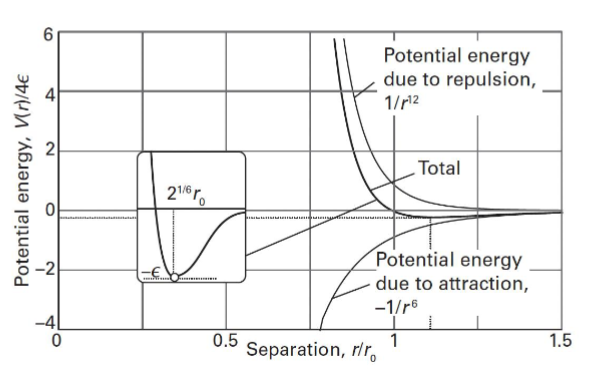
Lennard-Jones potential energy

Model of total intermolecular potential energy, including repulsion

Equation:

V=4(eplisom)(r_0¹²/r - r₀⁶/r) where r₀ is the separation when V=o and r is separation

The minimum on the Lennard-Jones potential energy diagram is the most stable, lowest energy state for the molecule and where attractive and repulsive forces are equal.

Relate the type of bonding and structure to key physical properties such as melting point, hardness, and electrical conductivity.

Describe how atoms or ions can be modelled as hard spheres in solids and how this leads to close-packed layers.

Atoms or ions can be modelled as spheres in solids. Spheres cannot fill all space: gaps always remain and so close packing gives an arrangement that minimises empty space.

Explain the concept of coordination number and its significance in determining the local environment of particles in solids.

Coordination number is the number of spheres immediately surrounding another sphere. Coordination number can give the type of structure and how efficiently spheres are arranged.

Molecular solid

Solid consisting of discrete molecules held together by van de Waals forces, possibly hydrogen bond

Covalent solid

Solid that forms an extended network through covalent bonds and the whole crystal system behaves like a giant molecule

Metal

Atomic orbitals overlap to form a band which is a set of molecular orbitals that are closely spaced with infinitesimally small gaps between orbitals and cover a finite range of energy. Electrons occupy the orbitals within the band.

Close packed layer

Layer of spheres arranged so there is a maximum utilization of space

Hexagonally close packed structure (hcp)

Structure is ABABAB… with third layer directly on top of first layer by placing second layer on up gaps of first layer and third layer on down gaps of second layer

Cubic close-packed structure (ccp)

Structure is ABCABC… Third layer is not directly above the first layer but instead above the gaps in the first layer. Again the second layer is on the up gaps of the first layer but the third layer is also on up gaps of second layer.

Capillary action

Tendency of liquids to rise up and down narrow tubes. If cohesion is greater than adhesion, moves down. If adhesion is greater than cohesion, rises up narrow tubes.

Nucleation

Provides surfaces to which molecules can attach and induce condensation

Colligative properties

Depends only on the number of solute particles present, not their identity.

Osmotic pressure

Minimum pressure that must be applied to a solution to stop the flow of solvent molecules (water) through a partially permeable membrane

Temperature-composition diagram

Phase diagram where the boundaries show the composition of the phases that are in equilibrium at various temperatures. Contain dew point line (top line, where last drop of liquid is - where condensation starts/end) and bubble point line (bottom line, where first bubble appears - where boiling starts)

Define state variables and apply the perfect gas law.

state variables are properties used to describe the state of a substance, including pressure, temperature, amount of substance and volume. Can give the perfect gas law.

Explain deviations from ideal behaviour using intermolecular forces.

Real gases deviate from ideal gas behaviour at low temperatures and high pressures - when intermolecular forces are non-zero. This is because at low temperatures, molecules no longer have sufficient kinetic energy to overcome their attractive intermolecular forces which means Z<1. At high pressures, molecules are forced closer together, volume of the molecules becomes significant and is no longer negligible, repulsive intermolecular forces dominate and Z>1.

Define dipoles, multipoles, and polarizability.

Dipoles - difference in electronegativity between two atoms creating a dipole moment.

Multipoles - combination of dipoles if more than one present (total overall dipole moment?)

Polarizability - how easily a molecule is distorted by a dipole moment/electric field. Larger molecules have greater electron density so are more polarizable.

Determine molecular polarity.

How polar a molecule is - depends on the difference in electronegativity of the atoms.

Explain how Gibbs free energy determines solid stability and melting behaviour.

At a certain pressure and temperature, the state with the lowest gibbs free energy is the most thermodynamically stable and has the least chemical potential. Melting occurs when the transition from solid to liquid produces a negative deltaG, meaning the liquid is more thermodynamically stable that the solid.

Identify tetrahedral and octahedral interstitial sites.

Tetrahedral sites: 3 spheres directly on top of 1 sphere.

Octahedral sites: 3 spheres on top of 3 spheres with the gap between spheres aligning to be on top of each other.

Recognise and describe simple cubic, bcc, and fcc unit cells.

Simple cubic: atoms only at cube verticies, coordination number of 6

Body centered cubic: atoms at cube corners and 1 at cube centre, coordination number of 8

Face centred cubic: atom at each corner of cube and in centre of each face, coordination number of 12

Explain why surface tension arises

Surface tension occurs because molecules at the top of a liquid experience unequal intermolecular forces - pulled down by the bulk below but only hit by gas molecules at top. Surface tension designed to minimise surface area: volume ratio.

Describe colligative properties and explain boiling point elevation, freezing point depression, and osmosis.

All colligative properties. Osmotic pressure is the pressure needed to stop osmosis, boiling point elevation occurs because molecules in the liquid get in the way of the molecules boiling off to gas, freezing point depression occurs because impure molecules get in the way of the regular layers that forms when a solid freezes.

Explain simple and fractional distillation using tie-line reasoning.

Simple distillation - good for when two mixtures have very different boiling points. One (more volatile) boils before the other, is condensed and collected and can be separated.

Fractional distillation - occurs when two mixtures have similar boiling points. Uses a fractional column and creates many small vapour-liquid equilibrium points. Boils, rises up fractioning column, condenses to a purer mixture and process repeats.

Define azeotropes and explain their impact on separations.

Azeotropes are mixtures that boil at a constant temperature and the vapour and liquid states have the same composition. Cannot be separated using simple or fractional distillation.