Derivatives of Trig Functions

(d)/(dx) sin (x)

cos (x)

(d)/(dx) cos (x)

-sin (x)

(d)/(dx) tan (x)

sec²(x)

(d)/(dx) cot (x)

-csc²(x)

(d)/(dx) sec (x)

sec(x)tan(x)

(d)/(dx) csc (x)

-csc(x)cot(x)

(d)/(dx) sin^-1u

(1/ sqrt(1-u²))(du)/(dx)

One divided by the square root of one minus u squared times the derivative of u (sin argument).

(d)/(dx) tan^-1u

(1/(1+u²))(du)/(dx)

One divided by one plus u squared times the derivative of u.

(d)/(dx) sec^-1u

(1/ ( |u| (sqrt(u²-1))(du)/(dx)

One divided by the absolute value of u times the square root of u squared minus one times the derivative of u. The absolute value of u must be greate than one.

(d)/(dx) cos ^-1u

(-1/ sqrt(1-u²))(du)/(dx)

Negative one divided by the square root of one minus u squared times the derivative of u (sin argument).

(d)/(dx) cot^-1u

(-1/(1+u²))(du)/(dx)

Negative one divided by one plus u squared times the derivative of u.

(d)/(dx) csc^-1u

(-1/ ( |u| (sqrt(u²-1))(du)/(dx)

Negative one divided by the absolute value of u times the square root of u squared minus one times the derivative of u. The absolute value of u must be greate than one.

(d)/(dx) e^u

e^u(du)/(dx)

e to the power of u times the derivative of u

(d)/(dx) a^u

a^u(ln(a))((du)/(dx))

a to the power of u times the natural log of a times the derivative of u.

Pneumonic Device: Princess Aulnadu

(d)/(dx) ln (u)

(1/u)(du/dx)

(d)/(dx) log_au

(1)/(u(ln(a)))((du)/dx))

One divided by u times the natural log of a time the derivative of u.

Pneumonic Device: Princess Ulnadu

Quotient Rule

lo d hi minus hi d lo all over lo lo

Physics Functions

Position

s(t)

Velocity

v(t) = s’(t)

Acceleration

a(t) = s’’(t) or a(t) = v’(t)

Jerk

j(t) = s’’’(t) or j(t) = a’(t)

Speed

|v(t)|

True Absolute Change

Δf=f(a+dx)-f(a)

Change in f equals f of a plus change in x minus f of a

True Relative Change

Δf/(f(a))

Change in f divided by f of a. (Change in f can be calculated by Absolute True Change equation)

True Percent Change

(Δf/(f(a))x100

Change in f divided by f of a times 100. (Change in f can be calculated by Absolute True Change equation)

Estimated Absolute Change

df=f’(a)dx

Estimated absolute change equals the derivative of f(a) times change in x.

Estimated Relative Change

df/f(a)

df divided by f(a) (df can be calculated by Estimated Absolute Change equation)

Estimated Percent Change

(df/f(a))x100

df divided by f(a) times 100

Average Mean Value

Calculates the average (mean) value

1/(b-a)∫(a,b)(f(x))(dx)

One divided by b minus a times the integral from a to b of f(x) dx

Difference Quotient

A formula that calculates the slope of a secant line between two points on a function

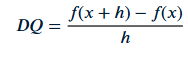
Horizontal Asymptotes

Compare degree of numerator to degree of denominator

If the degree of the denominator is higher than the degree of the numerator there is an asymptote at y=0

If the degrees of the numerator and denominatpr are equal, the asymptote is y = the ratio of the leading coefficients

If the degree of the numerator is higher than the degree of the denominator there is not horizontal asymptote

Vertical Asymptotes

To calculate vertical asymptotes of a rational function, simplify the function, crossing out like terms in the numerator and denominator and then set the denominator equal to zero and solve for x.

Intermediate Value Theorem

The Intermediate Value Theorem states that if a function f(x) is continuous on a closed interval [a, b], and N is a value between f(a) and f(b), then there exists a value c in the open interval (a, b) such that f(c) = N

If f(x) is continuous on and f(1) = 2 and f(5) = 8, then by the IVT, f(x) must take on the value 5 at some point between 1 and 5. 

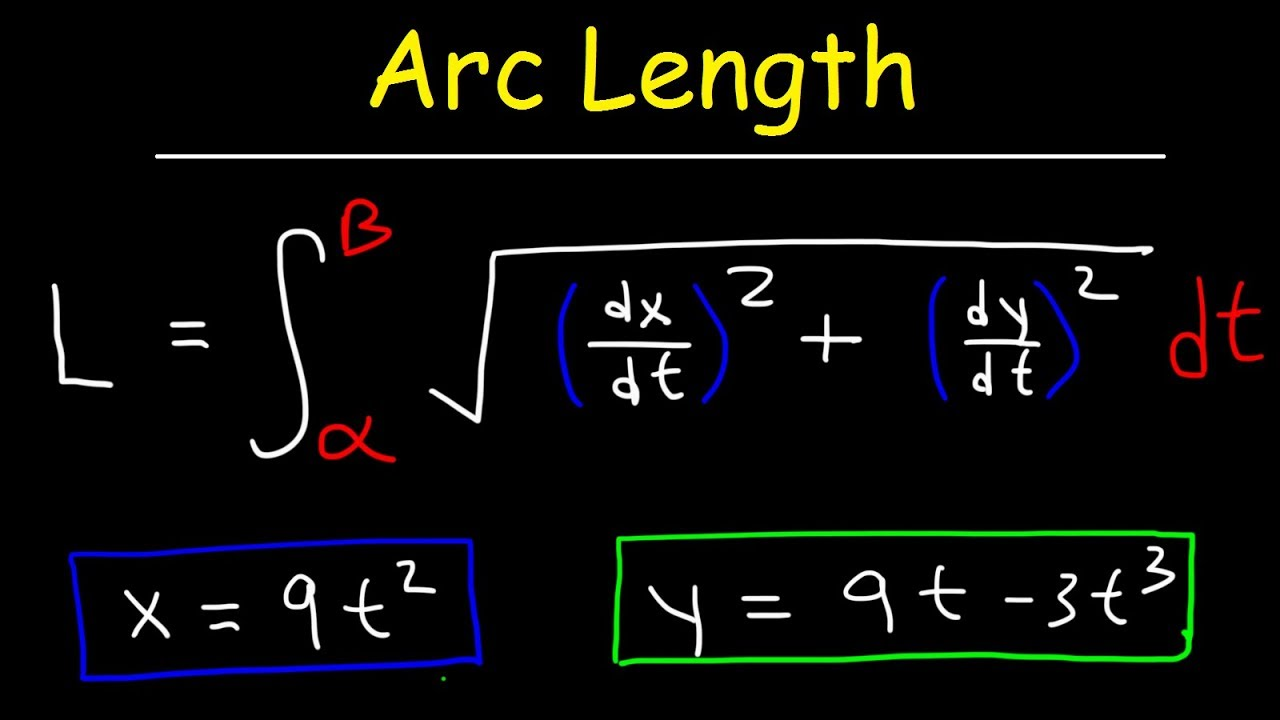
Length of a Path (Parametric)

Area of a Polar Curve

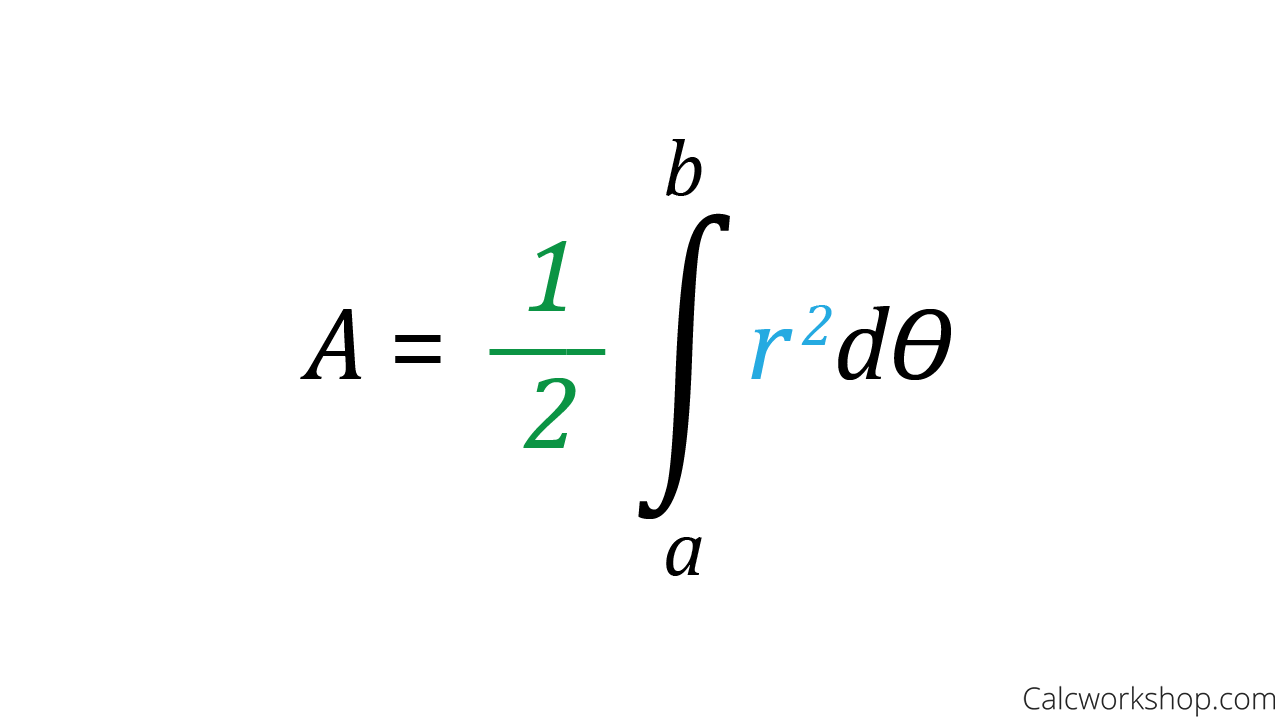
How to find where a particle is at rest

Calculate where velocity is zero

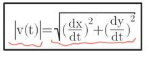
Parametric Equation for Speed

Mean Value Theorem

For a continuous function on a closed interval, there is some value c where the instantaneous slope (derivative) equals the average rate of change

The value c can be calculated by calculating the average rate of change of the function using the endpoints of the interval and the

(f(a)-f(b))/(a-b)

slope equation, then setting this equal to the derivative of the function and solving for x.

Derivative of Composite Functions

Implicit Differentiation

To implicitly differentiate, differentiate as normal, but write dy/dx next to every y you differentiate. After you have differentiated, isolate and solve for dy/dx.

To take the second derivative using implicit differetiation, use the same strategy as before, but for every dy/dx, plug in the first derivative. If you are evaluating the second dervative at a point, you can prematurely plug that point into dy/dx to keep calculations as simple as possible.

Inverse Functions

If g(x) is the inverse function of f(x),

g(x) = 1/f(x)

f(g(x))=x

If f(4)=2, g(2)=4

g’(x)=1/f’(x)

If f(4)= -8, then g’(-8)=1/f’(4)

Linearization Formula (used to calculate linear approximations)

L(x) = f(a) + f'(a)(x - a)

Where f(x) is the function, a is a point where you know the function value and derivative, and L(x) is the linear approximation of f(x) near a. 

When the second derivative of a function is concave up, the linearization of that equation with be an underestimate.

When the second derivative of a function is concave down, the linearization of that equation with be an overestimate.

When does a particle change direction?

When velocity changes sign

Distance Travelled

∫|v(t)| dt

The integral of the absolute value of the velocity function

When is the speed of a particle increasing?

When the sign of the acceleration is the same as the sign of the velocity

Extreme Value Theorem

A continuous function from a non-empty compact space to a subset of the real numbers attains a maximum and a minimum.

If a function is continuous on a closed interval [a, b], then it will have both an absolute maximum and an absolute minimum value within that interval

How to Find Max’s and Min’s with Derivatives

First Derivative Test

Differentiate the function f(x) to get f'(x). Set f'(x) = 0 and solve for x. These are the critical points. 

Choose test points to the left and right of each critical point. Evaluate f'(x) at these test points. 

If the point goes from + to -, it’s a local max

I the point goes from - to +, it’s a local min

Second Derivative Test

Find the critical points with the first derivative

Find the second derivative

For each critical point,

• If f''(x) is positive at a critical point, then it's a local minimum. 

• If f''(x) is negative at a critical point, then it's a local maximum. 

• If f''(x) is zero at a critical point, the test is inconclusive.
  

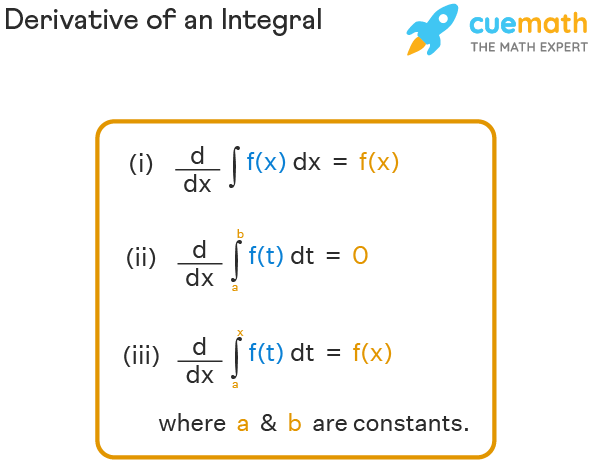
Derivative of an Integral