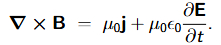Electromagnetism

Scalar

a physical quantity that only depends on magnitude

Vector

an object which is described by both a magnitude and a direction

Scalar field

a map between an N-dimensional space and a scalar quantity

Vector field 

a map between an N-dimensional space and an M-dimensional vector quantity.

What does the gradient of a scalar field represent

magnitude and direction of maximum increase of the scalar field

What is the gradient of a scalar field normal to?

lines (or surfaces) of constant field (contours) in direction of increasing field

What does (gradS) dotted with a unit vector of u represent?

the rate of change along the unit vector of u

What type of vector field is the result of the gradient on a scalar field?

A conservative field

What adjective describes any line integral over a conservative field?

path-independent

What value is given to any closed line integral in a conservative field?

Zero

What value is given to the curl of a conservative field?

Zero

What type of field is the divergence of a Vector field div V?

Scalar

What is the name of a vector field whose divergence is zero?

Solenoidal field

What type of field is the curl of a vector field?

Vector

What adjective is used to describe a vector field whose curl is zero?

Irrational

What type of result is yielded from the Laplacian acting on a scalar field?

scalar

What type of result is yielded from the Laplacian acting on a Vector field?

Vector

The result of the curl of a gradient of a scalar field curl(gradS)?

Zero

The result of the divergence of the curl of a vector field div(curl(v))

Zero

Principle of Superposition

The total field, E( r ), due to the individual electric fields associated to different individual charged particles, E_i ( r ), is obtained by adding together (or superposing) all the fields

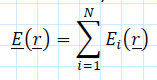
The electrostatic potential for a continuous charge distribution

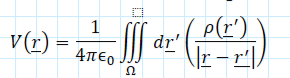
The electric field for a continuous charge distribution

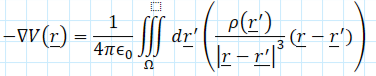
What are normal to the electric field lines?

The equipotential surfaces

In which direction to electric field lines point

From higher to lower potential

What equations of electrostatics relate potential to the charge densities?

Poisson Equation

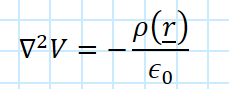
Gauss’ Law

The net electric flux through any closed surface equals the net electric charge within that surface, up to a factor

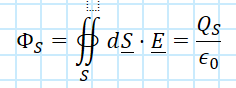
Divergence Theorem

The flux over a closed surface of a differentiable vector field equals the volume integral of the divergence of the field over the enclosed volume.

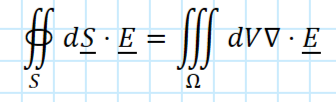
Stoke’s Theorem

The surface integral over an open bounded surface of the curl of a differentiable vector field equals the line integral of the curl of the field over the perimeter of the surface.

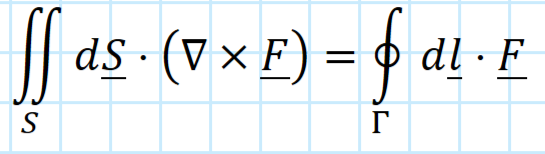
Force between charges q_1 and q_2 

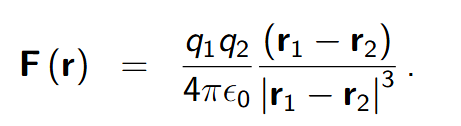
Electric field at any point due to charge q_1

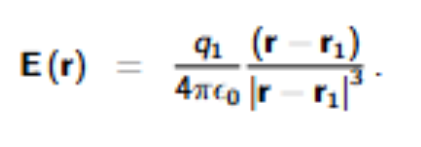
Relation between electric field and potential

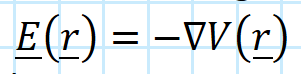
maxwells first equation

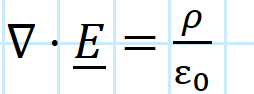
Maxwell 2

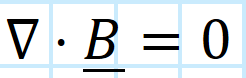
Maxwell 3

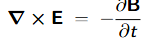
Maxwell 4