Graph Theory

EXAMPLE OF A GRAPH

defn of a graph

a graph G is a pair (V(G), E(G))

V(G)

• is a set

• elements of V(G) are the vertices of graph G

E(G)

• is a set

• elements of E(G) are the edges of the graph G

the sets V(G) and E(G) are linked by an

incidence function (see image)

• “e1 is incident to v1” if an end of e1 is connected to v1

defn of a loop

An edge e ∈ E(G) is a loop if ψ_G(e) = {v} for some vertex v ∈ V (G).

→ meaning both ends of the edge connects to the same vertex

defn of arc

An edge e ∈ E(G) is an arc if ψ_G(e) = {u, v}, for two distinct vertices u, v ∈ V (G).

• meaning an edge connecting two vertices together

parallel

Two edges e1 and e2 are parallel if ψ_G(e1) = ψ_G(e2)

• two edges connect together the same two vertices

defn of a simple graph

A graph is simple if it has no loops and no parallel edges.

adjacents

Two vertices u, v ∈ V(G) are adjacents (or neighbours) if there is an edge e ∈ E(G) such that ψG(e) = {u, v}. In this case, we write u ∼ v.

• meaning the vertices are connected by the same edge

An edge e ∈ E(G) is said to be ___________ to the vertices of ψ_G(e).

incident

adjacency matrix defn

Let G be a graph with n vertices v1, v2, ..., vn.

• An adjacency matrix of G is an n×n matrix A whose entry in row i and column j is equal to the number of edges linking vi and vj.

• see image for example

• note: there’s a 2 for entry (v1,v1) since both ends of e3 connects to v1

defn of a degree

Let G be a graph. The degree of a vertex v ∈ V(G), denoted by deg(v), is the number of edges incident to v, where loops on v are counted twice.

degree sequence

If V(G) = {v1, v2, ..., vn}, then the degree sequence of G is

(deg(v1), deg(v2), ..., deg(vn))

• the nums in a deg sequence can be in ANY ORDER

Handshake Lemma (formula)

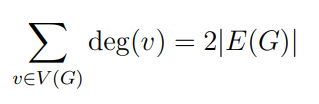
degree sequences are _______ to one graph

NOT unique; multiple graphs can have the same deg sequence

isomorphism concept

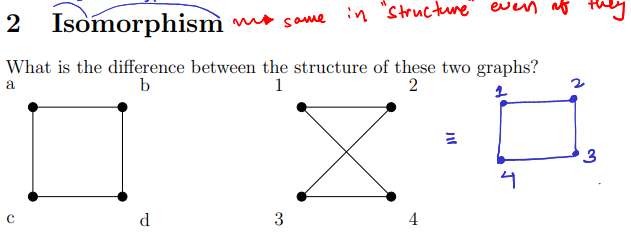
defn of isomorphism

Let G and H be two simple graphs. An isomorphism from G to H is a bijective function f : V (G) → V (H) such that for all u, v ∈ V (G), we have

u ∼ v ↔ f(u) ∼ f(v)

→ meaning adjacency properties are preserved

isomorphism basic example

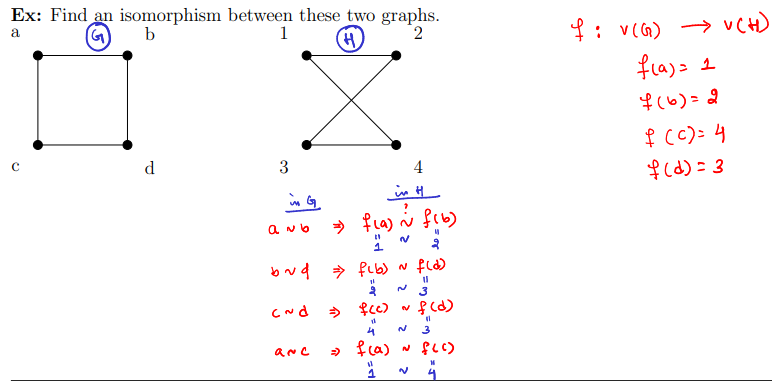
to show that two graphs are isomorphic

present an isomorphism between the two graphs

• show the bijective fn

• show the graph diagram

to show that two graphs G and H CANNOT be isomorphic

you must find a FUNDAMENTAL DIFFERENCE between G and H

the difference could be (verify in this order):

1. diff num of vertices

2. diff num of edges

3. diff deg sequence / diff num of elements in deg sequence

4. a subgraph of G that isn’t a subgraph of H

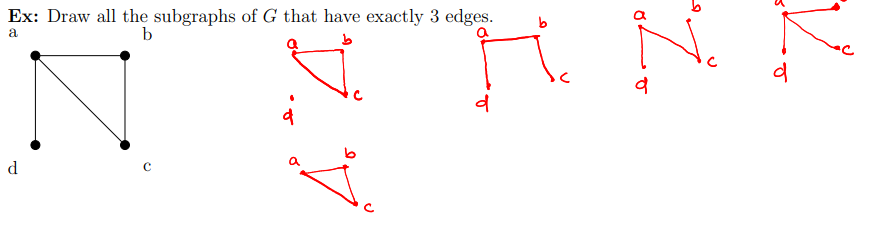
defn of a subgraph

Let G and H be two graphs. We say that H is a subgraph of G if V (H) ⊆ V (G) and E(H) ⊆ E(G). In this case, we write H ⊆ G

• the set of vertices of H is a subset of the set of vertices of G

• AND the set of edges of H is a subset of the set of edges of G

subgraphs visual

defn of a complete graph

let n be a positive integer (a natural num). the complete graph on n vertices, denoted by K_n, has the following properties:

• Kn is simple, |V(Kn)| = n → |V(K2)| = 2, meaning the graph of K2 has 2 vertices

• each pair of vertices is linked by one edge.

• every vertice is linked to every other vertice in the graph

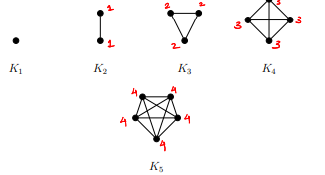
how many edges does a complete graph Kn have?

n “choose” 2

what is the deg sequence for a complete graph Kn?

(n-1, n-1, n-1, ….., n-1) → n - 1 repeated n times (since a complete graph of Kn has n vertices)

defn of a cycle

let n be a positive integer.

• a cycle of length n, denoted by C_n, is the following graph:

  • V(Cn) = {u1, u2, ..., un}. The vertex u1 is adjacent to u2 and to un.

  • The vertex u_n (the “last” vertice in the set of vertcies) is adjacent to u_n−1 and to u₁ (the first vertice).

  • For every other vertex, u_i is adjacent to u_i−1 and to u_i+1.

how many edges does a cycle graph Cn have?

n

• could think of a shape having the same number “sides” as vertices

what is the deg sequence of a cycle graph Cn?

(2, 2, 2, 2…..2) → repeated n times since a graph Cn has vertices