Week 5 (statistical inference)

Why do we standardise a number?

to improve its quality by making it consistent, accurate, and reliable for analysis, integration, and decision-making and compare it

How do we standardise a number?

with z-scores

What does the standard normal distribution look like?

e a symmetric, bell-shaped curve with its highest point at the center and its tails tapering off on both sides. standard distribution of 1 mean at 0.

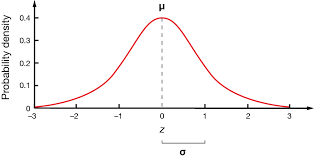
What do z scores and the standard normal distribution have to do with each other?

A z-score indicates how many standard deviations a value is from the mean, allowing for comparison of different data sets and the calculation of probabilities using z-tables and the standard normal curve. 

What are the two differences between calculating a z score for an individual and calculating it for a group of people?

the parameters used in the formula and the purpose of the calculation

Dispersion

tells us descriptive uncertainties

Descriptive statistics

• way of summarising what we know in a particular data set

• standard deviation

• range

Inferential statistics

• make predictions about a population based on a sample from that population

• using information we have in our data to draw conclusions about the population

• Inferential uncertainty

Inferential uncertainty 

• whether the pattern we find in our data is similar to what we’d find due to random processes

• result could have been produced by chance is very low than our uncertainty about our conclusions is low

• can’t calculate this

• so we calculate the probability that a random process could produce a pattern like the one we’ve found in our data

statistical inference

• we can use statistical inference to make statements about the unknown

• apply samples to whole population

• random process are highly predictable over the long time

• Test statistic 

• p value

test statistic

• information/error

• information is what is going on in the data

• error is all the reasons the data might be changing

• if the difference is big compared to the error we can be sure that something is going on

p value

• probability of a random process producing a pattern

• Once u know this we can make a decision about whether we think our data is just due to chance or if there is a meaningful pattern

Why are z scores useful?

• You can see where the score sits

• interpret a score meaningfully as it can compare to others

• can compare with other data as well (different measures)

• what proportion of people are scoring higher and lower

• represent how far the score is from the mean in standard deviation units