(9) Angular Kinematics

0.0(0)
studied byStudied by 0 people
learnLearn
examPractice Test
spaced repetitionSpaced Repetition
heart puzzleMatch
flashcardsFlashcards
Card Sorting

1/18

encourage image

There's no tags or description

Looks like no tags are added yet.

Study Analytics
Name
Mastery
Learn
Test
Matching
Spaced

No study sessions yet.

19 Terms

1
New cards

Angular kinematics

  1. units

    1. degree

    2. radian

  2. Quantities

    1. angular position and displacement

    2. angular velocity

    3. angular acceleration

  3. linear motion vs angular motion

    1. circular motion

2
New cards

Units

Degree

  • 1 revolution= 360°

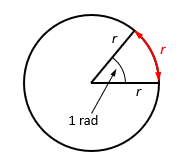
Radian

  • the angle with which the length of the arc becomes the same to the radius

  • 1 rad=57.30°

  • r=1rad

  • 2r=2rad

  • 3r=3rad

  • 2pi r= 2pi rad

  • 1 rev= 2pi rad= 360 degree

  • pi rad= 180 deg

  • pi/2 rad= 90 deg

  • pi/3 rad= 60 deg

  • pi/4 rad= 45 deg

  • pi/6 rad= 30 deg

pi=3.141592654

180/pi=57.29577951

<p>Degree</p><ul><li><p>1 revolution= 360<span>° </span></p></li></ul><p>Radian</p><ul><li><p>the angle with which the length of the arc becomes the same to the radius </p></li><li><p>1 rad=57.30<span>°</span></p></li><li><p>r=1rad</p></li><li><p>2r=2rad</p></li><li><p>3r=3rad</p></li><li><p>2pi r= 2pi rad</p></li><li><p>1 rev= 2pi rad= 360 degree</p></li><li><p>pi rad= 180 deg</p></li><li><p>pi/2 rad= 90 deg</p></li><li><p>pi/3 rad= 60 deg</p></li><li><p>pi/4 rad= 45 deg</p></li><li><p>pi/6 rad= 30 deg</p></li></ul><p>pi=3.141592654</p><p>180/pi=57.29577951</p>
3
New cards

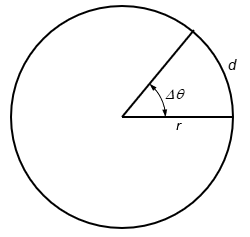
why radian?

simple relationship between the angle and length of the arc

  • d=r𐤃Θ

<p>simple relationship between the angle and length of the arc</p><ul><li><p>d=r<span>𐤃Θ</span></p></li></ul><p></p>
4
New cards

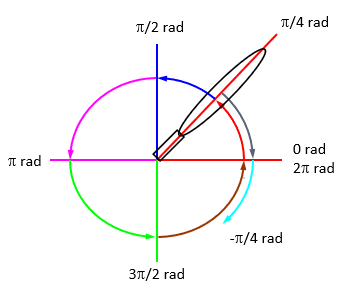
angular location at a given instant

  • unit: rad

  • direction

    • counterclockwise= +

    • clockwise= -

<ul><li><p>unit: rad</p></li><li><p>direction</p><ul><li><p>counterclockwise= +</p></li><li><p>clockwise= - </p></li></ul></li></ul><p></p>
5
New cards

angular displacement

  • change in angular position

    • net effect of angular motion

  • unit: rad

  • direction

    • counterclockwise: +

    • clockwise:-

  • zero angular displacement

    • no net rotation 𐤃Θ= Θ2-Θ1=0

    • no rotation dΘ= Θ2-Θ1=0

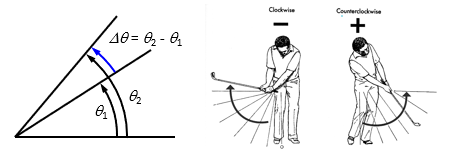
<ul><li><p>change in angular position</p><ul><li><p>net effect of angular motion</p></li></ul></li><li><p>unit: rad</p></li><li><p>direction</p><ul><li><p>counterclockwise: +</p></li><li><p>clockwise:- </p></li></ul></li><li><p>zero angular displacement</p><ul><li><p>no net rotation 𐤃Θ= Θ<sub>2</sub>-Θ<sub>1</sub>=0</p></li><li><p>no rotation dΘ= Θ<sub>2</sub>-Θ<sub>1</sub>=0</p></li></ul></li></ul><p></p>
6
New cards
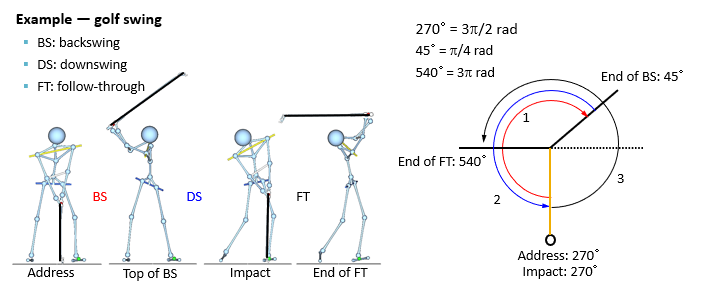
<p>example of angular displacement </p>

example of angular displacement

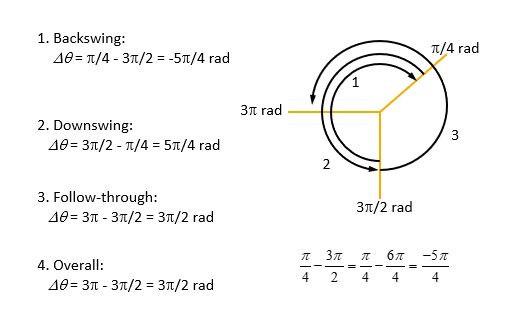
knowt flashcard image
7
New cards

Angular velocity

  • rate of change in angular position

  • angular displacement/time

  • direction

    • positive: counterclockwise rotation

    • negative: clockwise rotation

  • vector

  • unit: rad/s

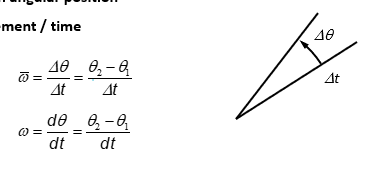
<ul><li><p>rate of change in angular position</p></li><li><p>angular displacement/time </p></li><li><p>direction </p><ul><li><p>positive: counterclockwise rotation </p></li><li><p>negative: clockwise rotation </p></li></ul></li><li><p>vector </p></li><li><p>unit: rad/s</p></li></ul><p></p>
8
New cards

zero angular velocity

  • zero average angular velocity: no displacement=no net motion

  • zero instantaneous angular velocity: no motion=constant angular position

<ul><li><p>zero average angular velocity: no displacement=no net motion</p></li><li><p>zero instantaneous angular velocity: no motion=constant angular position</p></li></ul><p></p>
9
New cards

angular acceleration

  • rate of change in angular velocity

    • a(bar)= 𐤃ω/𐤃t= ω2-ω1/𐤃t a= dω/dt= ω2-ω1/dt

  • positive angular acceleration

    • speed-up of counterclockwise ω

    • slow-down of clockwise ω

  • negative acceleration

    • Slow-down of counterclockwise ω

    • speed up of clockwise ω

  • vector

  • unit: rad/s2

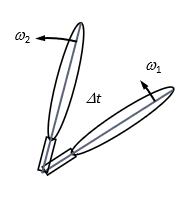
<ul><li><p>rate of change in angular velocity</p><ul><li><p>a(bar)= <span>𐤃</span><strong>ω/</strong><span>𐤃t= </span><strong>ω<sub>2</sub>-ω<sub>1</sub>/</strong>𐤃t a= d<strong>ω/dt= ω<sub>2</sub>-ω<sub>1</sub>/dt</strong></p></li></ul></li><li><p>positive angular acceleration</p><ul><li><p>speed-up of counterclockwise <strong>ω</strong></p></li><li><p>slow-down of clockwise <strong>ω</strong></p></li></ul></li><li><p>negative acceleration</p><ul><li><p>Slow-down of counterclockwise <strong>ω</strong></p></li><li><p>speed up of clockwise <strong>ω</strong></p></li></ul></li><li><p>vector</p></li><li><p>unit: rad/s<sup>2</sup></p></li></ul><p></p>
10
New cards

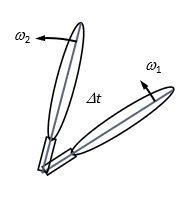
zero angular acceleration

a(bar)= 𐤃ω/𐤃t= ω2-ω1/𐤃t =0 a= dω/dt= ω2-ω1/dt= 0

  • zero average a: no net change in ω

  • zero instantaneous a: constant ω

<p>a(bar)= 𐤃<strong>ω/</strong>𐤃t= <strong>ω<sub>2</sub>-ω<sub>1</sub>/</strong>𐤃t =0 a= d<strong>ω/dt= ω<sub>2</sub>-ω<sub>1</sub>/dt= 0</strong></p><ul><li><p>zero average a: no net change in <strong>ω</strong></p></li><li><p>zero instantaneous a: constant <strong>ω</strong></p></li></ul><p></p>
11
New cards

example angular acceleration

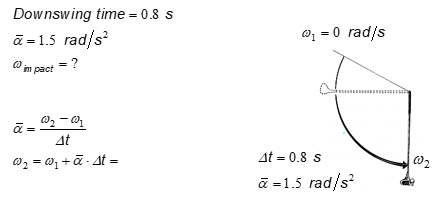
knowt flashcard image
12
New cards

linear vs angular quantity differences

<p></p>
13
New cards

circular motion

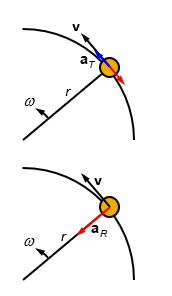
directions

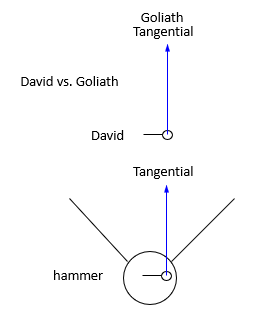
  • tangential (T): along the tangent

  • radial (R): Along the radius, perpendicular to the tangent

14
New cards

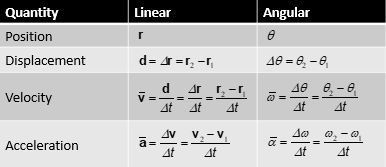
Velocity relationship

  • direction of the linear velocity: tangential

  • magnitude of the linear velocity

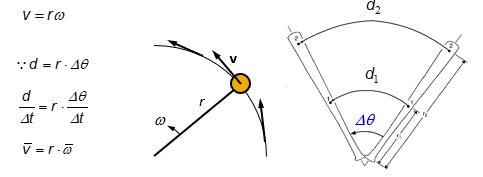
<ul><li><p>direction of the linear velocity: tangential</p></li><li><p>magnitude of the linear velocity </p></li></ul><p></p>
15
New cards

velocity relationship cont.

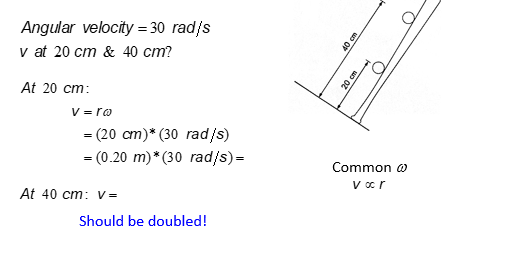
  • for a given ω: v is proportional to r

    • v=rω

    • v∝r

  • for a given r: v is proportional to ω

    • v=rω v∝ω

    • to hit the ball farther, one has to swing the bat faster

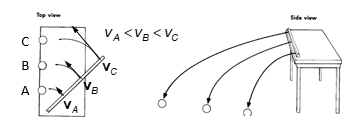
<ul><li><p>for a given <strong>ω: </strong>v is proportional to r </p><ul><li><p>v=r<strong>ω</strong></p></li><li><p>v<span>∝r</span></p></li></ul></li><li><p>for a given r: v is proportional to <strong>ω</strong></p><ul><li><p><span>v=<strong>r</strong></span>ω v<span>∝</span><strong>ω</strong></p></li><li><p>to hit the ball farther, one has to swing the bat faster </p></li></ul></li></ul><p></p>
16
New cards

velocity relationship cont. pt 2

  • for a give v: r and ω are inversely proportional to each other

    • v=rω ω∝1/r

    • v remains constant

    • r decreases —→ ω increases

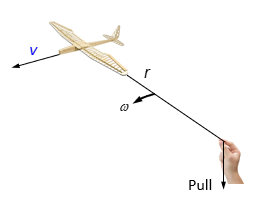
<ul><li><p>for a give v: r and <strong>ω</strong> are inversely proportional to each other </p><ul><li><p><strong>v</strong>=rω ω∝1/r</p></li><li><p>v remains constant </p></li><li><p>r decreases —→ ω increases </p></li></ul></li></ul><p></p>
17
New cards

example: Slinging and hammer throw

knowt flashcard image
18
New cards

example: batting

knowt flashcard image
19
New cards

two different kinds of acceleration

acceleration relationship

  • tangential acceleration

    • due to the change in speed (magnitude of v)(speed up or slow)

    • aT= ra= v2-v1/𐤃t

  • radial acceleration

    • due to the change in the direction of v

    • aR=rω2= v2/r

    • towards the center of rotation: centripetal acceleration

<p>acceleration relationship</p><ul><li><p>tangential acceleration</p><ul><li><p>due to the change in speed (magnitude of v)(speed up or slow)</p></li><li><p>a<sub>T</sub>= ra= v<sub>2</sub>-v<sub>1</sub>/𐤃t</p></li></ul></li><li><p>radial acceleration</p><ul><li><p>due to the change in the direction of v</p></li><li><p>a<sub>R</sub>=rω<sup>2</sup>= v<sup>2</sup>/r</p></li><li><p>towards the center of rotation: centripetal acceleration</p></li></ul></li></ul><p></p>

Explore top notes

Explore top flashcards