WJEC AS Physics - Unit 2.4, 2.5 + 2.6

Progressive wave

A pattern of disturbances travelling through a medium and carrying energy with it, involving the particles of the medium oscillating about their equilibrium positions

2 types of progressive waves

Transverse and Longitudinal

Transverse wave

A transverse wave is one where the particle oscillations are at right angles to the direction of travel (or propagation) of the wave

Longitudinal wave

A longitudinal wave is one where the particle oscillations are in line with (parallel to) the direction of travel (or propagation) of the wave

Polarised wave

A polarised wave is a transverse wave in which particle oscillations occur in only one of the directions at right angles to the direction of wave propagation

Examples of transverse waves

• Water waves

• Waves on a spring

• All EM waves

Examples of longitudinal waves

• Sound waves

• P-waves (seismic waves)

Displacement of a wave

Displacement is the shortest distance of a wave particle from its equilibrium position

Amplitude of a wave

Amplitude is the maximum displacement of a wave particle

Phase of a wave

If a particle along the wave is in phase with another, then it means that they are in the same point in the cycle at the same time. If they are at the opposite points in the cycle at the same time then they are called anti phase

Period of a wave

The time of one complete cycle. It is related to the frequency by the equation T=1/f. Where T=the period and f=the frequency

Speed of a wave

The distance that the wave profile moves per unit time

Equation for the speed of a wave

c=fλ

Wavelength of a progressive wave

The wavelength of a progressive wave is the minimum distance (measured along the direction of propagation) between two points on the wave oscillating in phase

Frequency of a wave

The frequency of a wave is the number of cycles of a wave that pass a given point in one second [or equivalently the number of cycles of oscillation per second performed by any particle in the medium through which the wave is passing]

How wavefronts can be produced

Using a ripple tank

What is always perpendicular to the wavefront

The direction of propagation

Distance between adjacent wave front is what

Wavelength

All the points on a wave front oscillate in what

Phase

The frequency of wave fronts

The frequency is the number of wave fronts that pass a point per second

Polarisation

The effect of passing light though a polarising filter

How many planes of vibration will a polarisation filter allow to pass

One

What polarisation does to light

Cause it to become plane polarised

Wave type with which polarisation will only occur

Transverse

Result of placing two Polaroid filters so that their angles of polarisation are at 90 degrees to each other

No transmission of light

What cross polaroids are used in

Stress analysis using plastic structures as a model

What appears when a plastic model is placed between two filters as one is turned relative to the other

Coloured lines of stress

In phase

Waves arriving at a point are said to be in phase if they have the same frequency and are at the same point in their cycles at the same time.

Wave sources are in phase if the waves have the same frequency and are at the same point in their cycles at the same time, as they leave the sources

Diffraction

Diffraction is the spreading out of waves when they meet obstacles, such as the edges of a slit. Some of the wave’s energy travels into the geometrical shadows of the obstacles

Principle of superposition

The principle of superposition states that if waves from two sources [or travelling by different routes from the same source] occupy the same region then the total displacement at any one point is the vector sum of their individual displacements at that point

Constructive interference

When the same parts of two waves from coherent sources occupy the same space e.g. 2 troughs or 2 crests

Destructive interference

When opposite parts of two waves from coherent sources occupy the same space e.g. a trough and a crest

Interference pattern

When waves from two identical sources meet

Coherent sources

Sources where everything about the sources are identical

How an interference pattern is produced

Alternate lines of constructive and destructive interference

Because the sources in an interference pattern are identical, what are the lines of constructive and destructive interference?

Fixed

If the sources of an interference pattern is light, how could it be displayed on screen?

Alternating dark and bright fringes

What is used to show interference

2 coherent sources of light

What the Young’s double slit experiment show

• light has a wave nature

• Allows for the measurement of wavelengths of light

Equation for Young’s double slit experiment

Δy=Dλ/a

Rearrangement of equation for Young’s double slit experiment

λ=aΔy/D

Assumptions that Young’s double slit experiment equation relies on

D > a

change in y > a

Path difference at O in Young’s double slit experiment is given by

S2O-S1O=0

Meaning of path difference being given by S2O-S1O=0

The constructive interference will take place at O and be a bright band

Must be whole number of what for a bright band to appear at P

Wavelengths difference between S2P and S1P

In Young’s double slit experiment, for a bright band to appear at P there must also be a whole number of wavelengths difference between S2P and S1P. This causes what equation to be true?

S2P-S1P=nλ but if P is the next bright band to O then S2P -S1P = λ since n=1

Path difference at O for a dark band to appear

Half a wavelength difference

For a dark band to appear then the path difference at O must be half a wavelength difference. This causes what equation to be true?

S2O - S1O = λ/2 and general for an any dark band S20 - S1O = λ (1/2 + n)

Diffraction effect if λ < d

Little diffraction

Diffraction effect if λ =d or λ > d

Wave spreads as roughly semicircular wavefronts

Diffraction effect if λ > d

The main beam spreads

Advantages diffraction has over an interference pattern

• the order/lines are much further apart - the measurement of the angle is easier and more accurate (less uncertainty)

• Because a diffraction grating is used it makes the beams/orders much brighter/the larger number of slits makes it brighter

• A large number of slits makes the beams sharper/more focused

What the advantages diffraction has over an interference pattern

The separation, d, of the slits/gaps is very small

Diffraction grating

A plate on which there is a very large number of parallel, identical, very closely spaced slits

Pattern produced if monochromatic light is incident on the plate of a diffraction grating

A pattern of narrow bright lines is produced

Diffraction grating works on same principle as what

The double slit experiment

Equation for diffraction gratings

d sinθ= nλ

Stationary wave

A pattern of disturbances in a medium, in which energy is not propagated. The amplitude of particle oscillations is zero at equally-spaced nodes, rising to maxima at antinodes, midway between the nodes

Nodes

The places on a wave where the amplitude of particle oscillations is zero

Antinodes

The places on a wave where the maximum amplitude of particle oscillations occurs

Intermodal distance

The distance between two adjacent nodes

Intermodal distance is equal to

Half a wavelength

Method for determining the speed of sound in air

1. Use a selection of tubing forks and find the 1st position of resonance (where the sound of the fork suddenly increases)

2. Length L is measured (tube out of water)

3. Frequency of the fork is noted

4. Each measurement is repeated and mean L is calculated

1st position of resonance in determining the speed of sound of air

λ/4 of a stationary wave

Equation for determining the speed of sound of air practical

λ/4 = l+e

Where l= total length pit of water, e=end correction (distance between tuning fork and open ended cylinders top)

Energy transfer properties in stationary waves

Energy is stored not transferred

Energy transfer properties in progressive waves

Energy is transferred along the wave

Amplitude of stationary waves

It varies from zero at nodes to maximum at antinodes

Amplitude of progressive waves

Is the same for all particles within a wave

Frequency of stationary waves

All particles oscillate at the same frequency except those at nodes

Frequency of progressive waves

All particles oscillate at the same frequency

Wavelength of stationary waves

Equal to twice the distance between adjacent nodes

Wavelength of progressive waves

equal to the distance between adjacent particles at the same phase

Phase difference between 2 particles in stationary waves

Points between nodes are in phase. Points on either side of a node are out of phase

Phase difference between 2 particles in progressive waves

Points exactly a wavelength (2 intermodal distances) apart are in phase. The phase of points within a wavelength can be 0 to 360

Diagram for determining speed of sound in air

Phase difference

The difference in position of 2 points within a cycle of oscillation. Given as a fraction of the cycle or as an angle, where one whole cycle is 2π or 360 degrees, together with a statement of which point is ahead in the cycle

Coherence

Waves or wave sources, which have a constant phase difference between them (and therefore must have the same frequency) are said to be coherent

Stationary wave

A pattern of disturbances in a medium, in which energy is not propagated. The amplitude of particle oscillations is zero at equally-spaced nodes, rising to maxima at antinodes, midway between the nodes

Refractive index

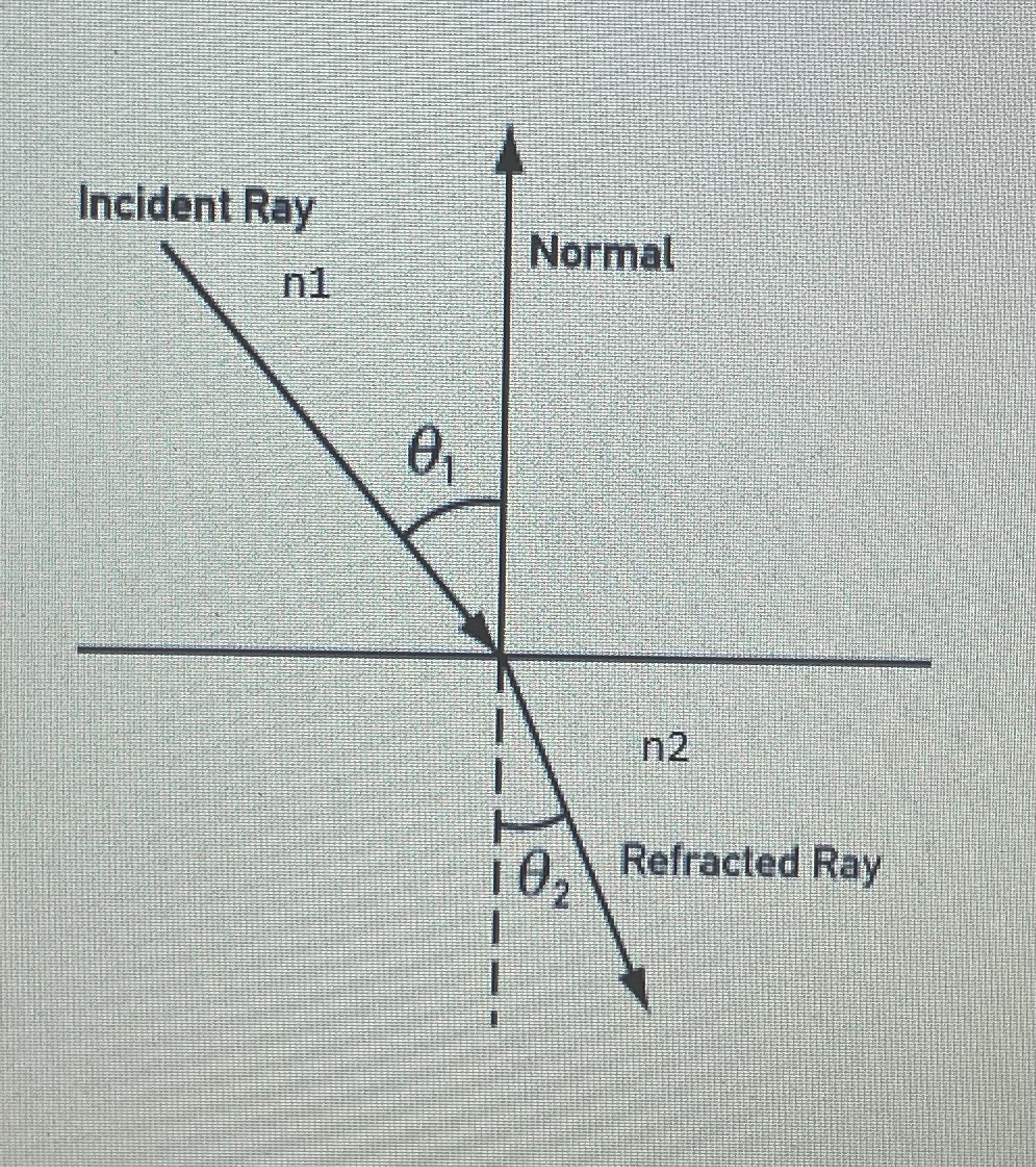
For light, Snell’s Law may be written n1 sinθ1=n2 sinθ2 in which θ1 and θ2 are angles to the normal for light passing between medium 1 and medium 2; n1 and n2 are called the refractive indices of medium 1 and medium 2 respectively. The refractive index of a vacuum is fixed by convention as exactly 1

Snell’s Law

At the boundary between any two given materials, the ratio of the sine of the angel of incidence to the sine of the angle of refraction is constant

Critical angle

When light approaches the boundary between two media from the ‘slower’ medium, the critical angle is the largest angle of incidence for which refraction can occur. The refracted wave is then travelling at 90 degree to the normal

Refraction

Light changes direction as it goes from one medium to another

Equation for refractive index

n=c/v

Where c= speed of light and v=speed of light in a medium

Diagram for Snell’s Law

Total Internal Reflection

When light moves from a more optically dense material to a less optically dense material causing a change in speed of light

Critical angle and total internal reflection

When the incident angel is greater than the critical angle, TIR occurs

Conditions for total internal reflection

• n1 > n2; light must travelling from a medium of higher refractive index to a medium of a lower refractive index

• θ1 > θc; angle of incidence must be greater than critical angle

Fibre optics

• TIR occurs

• n1 sinθ1 = n2

• Different pathways are called modes

• Number of possible pathways = multimode fibre

• A monomode fibre has only one pathway

Monomode fiber

A fibre with only one pathway

Multimode fiber

Number of possible pathways in the fibre

Advantages of monomode fibres

• longer lengths and faster/higher rates of data transfer

Disadvantages of monomode fibres

Very expensive

Advantages of multimode fibres

Disadvantages of multimode fibres

• light hits the boundary between the core and cladding of the angle between the light ray and axis is small; TIR occurs and so there is no loss of light from the fibre

• The paths are at different angles and therefore have different path lengths; they arrive at the other end at slightly different times - the pulse is spread out and smeared

• Repeated pulses will overlap which means they will spread out and cause multimode dispersion; to avoid this data transfer must be slower and the distance must be shorter