Unit 3 AP precalculus

Sin²x + cos²x =

1

Sin(α ± β) =

sin(α)cos(β) ± cos(α)sin(β)

Sin(2θ) =

2sin(θ)cos(θ)

Cos(2θ) =

Cos²(θ) - sin²(θ)

Cos(π/2 - θ) or Cos(θ - π/2) =

Sin(θ)

sin(-θ) =

-sin(θ)

Cos(-θ) =

Cos(θ)

cos (a ± B) =

cos (a)cos(ß) -(±) sin(a)sin(B)

how to express complex numbers with polar coordinate (r,θ)

rCos(θ) + iSin(θ)

sin(π/3)

√3/2

cos(π/3)

1/2

Formula for angle in radians

(Arc length)/radius

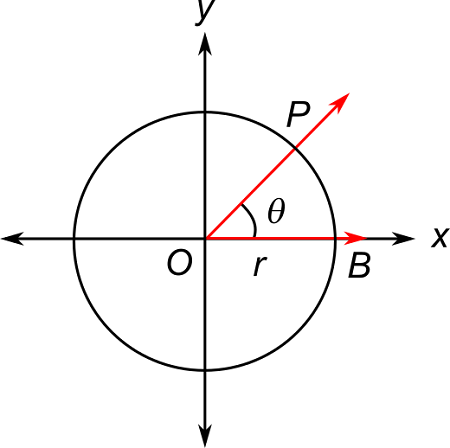
Sin(θ) is the ratio of

The vertical displacement of P from the x-axis to the distance between the origin and point P

Cos(θ) is the ratio of

The horizontal displacement of P from the y-axis to the distance between point P and the origin

Given an angle in standard position the tangent of the angle is the same as

The slope of the terminal ray

Cos(θ) in terms of sin(θ)

Sin(θ + π/2)

Sin(θ) is even or odd

odd

Cos(θ) even or odd

Even

Range of secant and cosecant

(-oo, -1] U [1, oo)

arcsinx in terms of arcos

arcos(√(1 - x²))

If a polar function is positive and decreasing or negative and increasing then

The distance between the function and the origin is decreasing