Multivariable Calculus - Lecture #2

Dot product, Orthogonal Projection, Cross product,

given vectors a: ⟨ a1, a2,a3 ⟩ and b: ⟨ b1, b2,b3 ⟩

Dot Product: 2 ways to find it

if you are given components:

if you are given angle between the 2 vectors:

it gives a ____

scalar

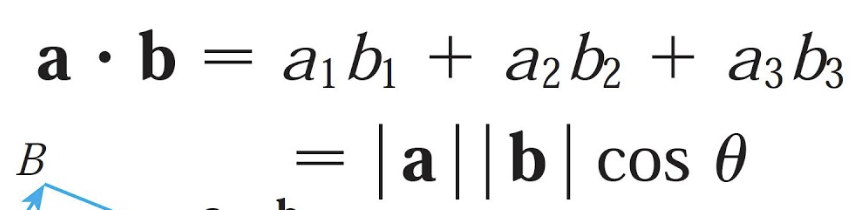
Properties:

1. v⋅w

2. v⋅(u+w)

3. (cv)⋅w

4. v⋅v = ____ thus |v| = _____

w⋅v

v⋅u + v⋅w

c(v⋅w) = v⋅ (cw)

|v|² (≥0 for all v), √(v⋅v)

θ =angle between the vectors =

θ restriction

if θ = 0 or π, then the vectors are _____

if θ = π/2, then the vectors are _____

0 ≤θ ≤ π

parallel

orthogonal

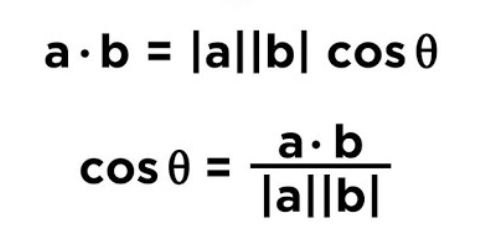
How to prove parallel vectors

How to prove perpendicular (orthogonal vectors)

scalar multiples

dot product is 0

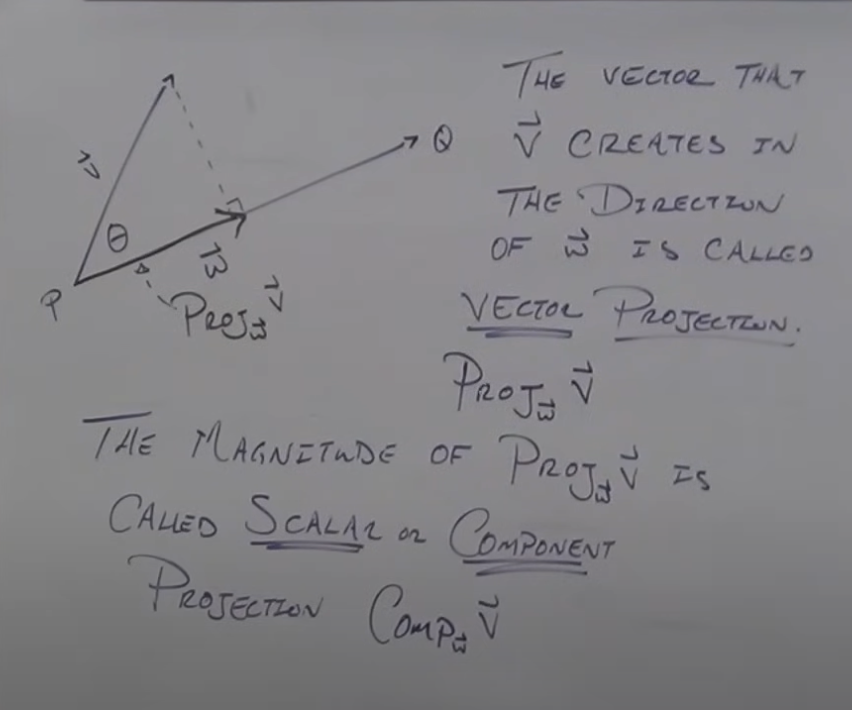
The vector that vector v creates in the direction of vector w is called the _______.

The magnitude of the vector projection is called the _____.

vector projection

scalar/component projection

scalar/component projection 2 formulas:

It is positive for an ___ angle and negative for an ____ angle).

acute, obtuse

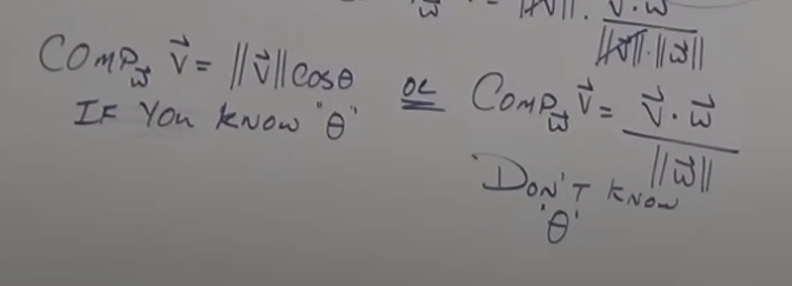
vector projection of v in the direction of u formula

the one youre projecting onto has the ____

magnitude * direction

scalar * vector

direction

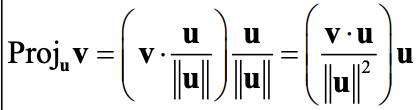
Work = _____ = ___

|f||d|cosθ, f⋅d

direction cosines

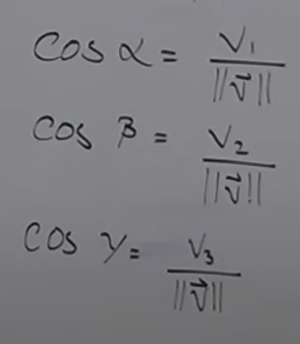
how to find unit vector from direction cosines

Cross product: u x v

2 ways to find it

if you have component form:

if you know angle θ btwn u and v:

it gives a ____

|u||v|sinθ * unit vector perp to u and v

vector

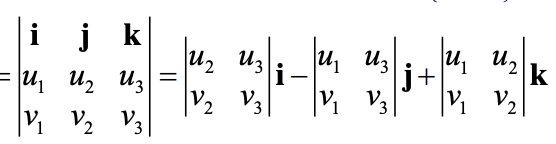
u x v is a vector _____ to both u and v

____ is ALSO a vector orthogonal to u and v

u x v = ____(v x u)

orthogonal

v x u

-

if a⋅b = 0

if a x b = 0

a and b are orthogonal

a and b are parallel

|u x v| =

|u||v| sinθ

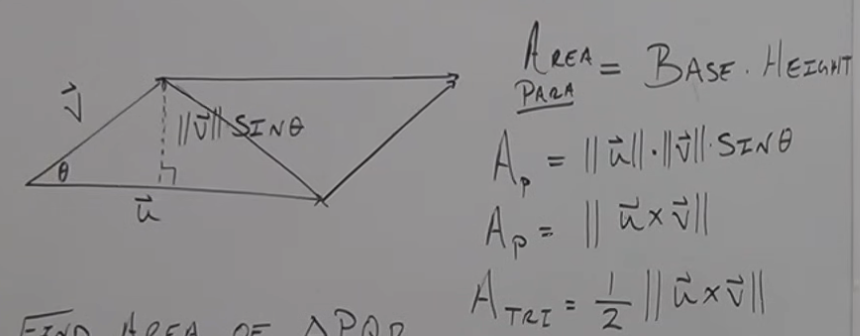
Area of parallelogram and area of triangle given two vectors that go from the same point

magnitude of cross product

magnitude of cross product / 2

algebraic properties of the cross product: suppose u, v, and w are vectors in R3 and t is a scalar

1. v x u = ___ u x v (corollary: u x u = ___)

2. u x (v+w) = _____, (u+v) x w = _____

3. (tu) x v = t(u x v) = u x (tv)

4. u x 0 = ___

5. u⋅(v x w) = ____ (triple scalar product)

6. u x (v x w) = _______ (triple vector product)

-

u x v + u x w, u x w + v x w

0

(u x v)⋅w

(u⋅w)v-(u⋅v)w

triple scalar product: volume of parallelepiped formed by

vectors u, v, w

V = _____

How to find the triple scalar product:

|u⋅(vxw)| note the brackets mean abs value

Do cross product v x w but replace i j k with u1 u2 u3

if u⋅(v x w) = 0, then u, v, and w are

coplanar

|τ| =

|f| |r| sinθ