ECONOMETRICS

What does regression do?

Minimizes SSR

SSR formula

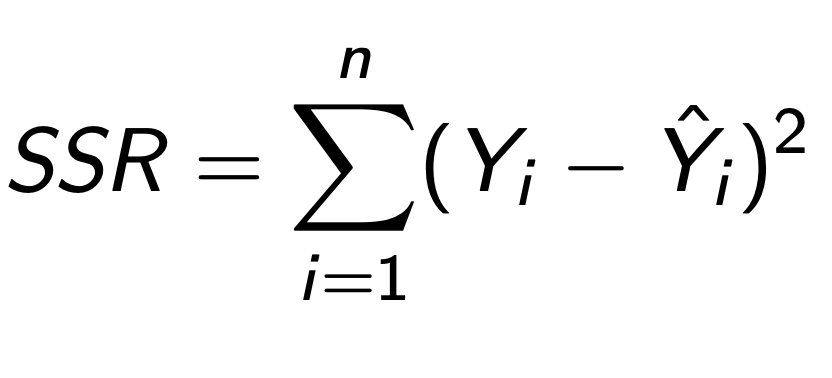
Normal equations

solution of SSR, derivatives of SSR wrt to alpha/beta

FOC wrt alpha 

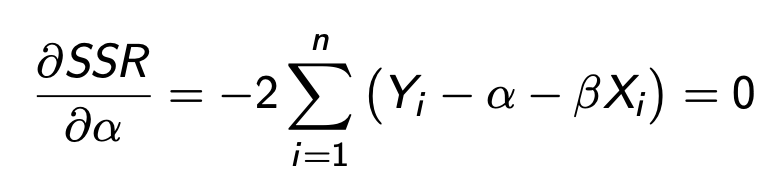
FOC wrt beta

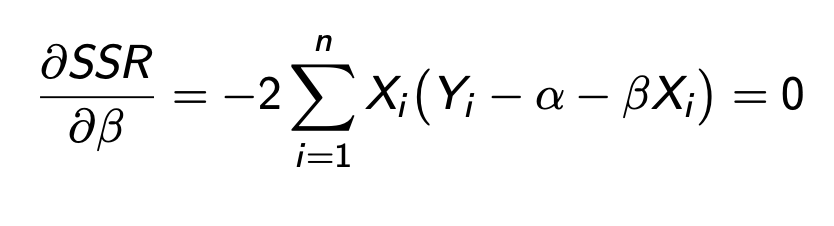
Beta

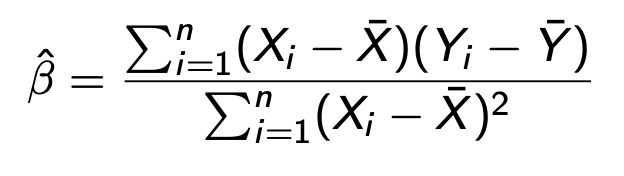
Or cov(x,y)/var(x)

Alpha

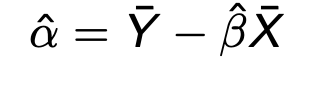
Sample covariance

measures relation between 2 random variables

Sample variance

spread of data

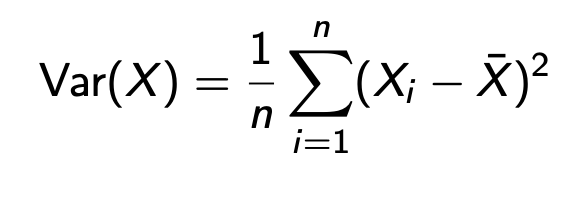
SST

Total Sum Squares

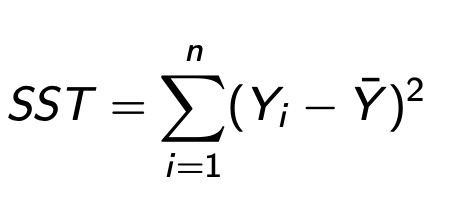
SSE

Explained Sum of Squares

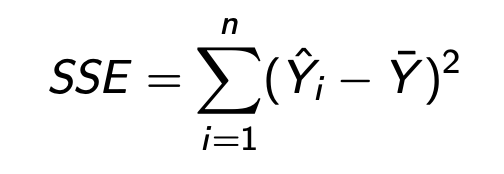
SSR

Residual Sum of Squares

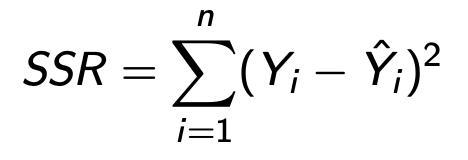
Coefficient of Determination

R² proportion of variation explained by regression

SSE/SST 1 - SSR/SST

Goodness of fit

Gauss Markoff Assumptions 

OLS: linearity, random sampling, …

Standard Error

sigma² = SSR/(n-2)

Standard error of beta

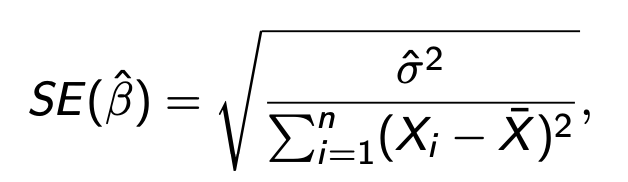
Stanard error of alpha

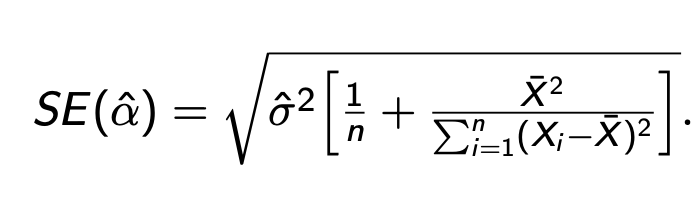
t test hypothesis

Ho: B = Bo
Ha: B ≠ Bo

if tcrit (wrt 1-alpha/2 and df - 2) < t reject ho

t

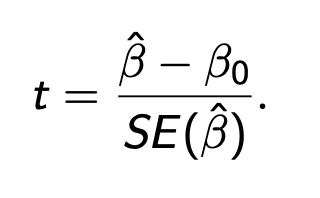
Confidence Interval

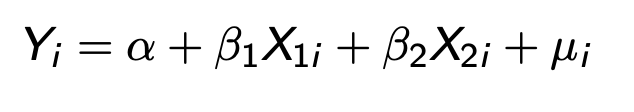
Coeffs in regression with mmultiple parameters

Partial effects

Effect of Xi on Y holding X2 constant and vv

Take deriv wrt each B to get new beta

Adjusted R²

R² automatically inflates artificially, R² bar (adj) penalizes irrelevant regressors

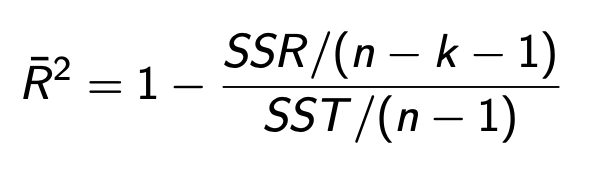
Omitted var bias, what is effect on included coeff?

omitting relevant vars that are related to vars in model creates bias for coeff in existing vars

effect on existing vals (if there is relation bt X1/X2

LOOK AT NOTES FOR MATRIX FORM

Du

Dummy Variables

allos to handle cat vars and encodes qualitative characteristics

Interaction term

lets us see affect of 1 var to depend on another

beta (x1*x2)

ex if education * male, beta is diff in return to educ bt men/somen

What are the 5 assumptions of OLS

Random sampling, linearity in param, no perfect multi-collinearity, zero conditional mean, homoskedasticity

A: Random sampling, what happens if it is violated?

all xi/yi come from same pop drawn independenly

sample is representative of pop

2. biased estimates

A: Linearity in parameters

x/y relation doesnt have to be linear but parameters must enter linearly
y = alpha + beta x² + u is stil linear in parameter

A: Zero cond mean

error has mena zero —> all determinatns are captured and only pure noise remains

A: Homoskedasticcity

variance X depend on any regressor 

Gauss Markov Theorem

under classic linear reg assumptions
(linearity, expected mean = 0 and homeoskedasticity)

then OLS estimators (a/b) are BEST LINEAR UNBIASED ESTIMATORSB

BLUE

Best linear unbiased estimators
- Linear: expressed as linear combination of Y
- unbiased (expected val of alpha/beta = a/b)
- best: minimum variance among all linear unbiased estimators

Unbiased

expected value of estimator B is B 

Consistency

consistent if predicted value converges to real value as sample size approaches infinity

Perfect vs near MC

one regressor is exact linear combo of others other is very close (high corr)

CANNNOT ESTIMATE MODEL IN PERFECT MC

Aux regression for perfect MC

Residual variation must be positive otherwise for R²j we have perfect MC

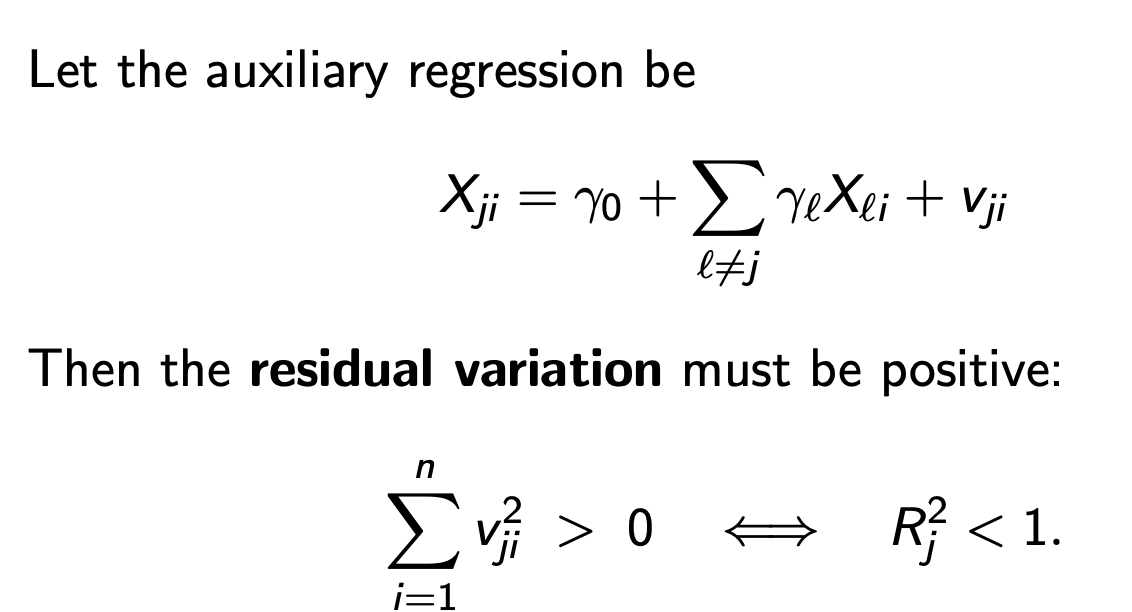
What does MC near do/not do

DOES NOT BIAS OLS COEFFICIENTS

Does:

• increase var

• wide CI

• small t

• makes coeff sensitive

VIF 

Variance Inflation Factor 

Rj² is from aux reg of Xj on all other regressors 

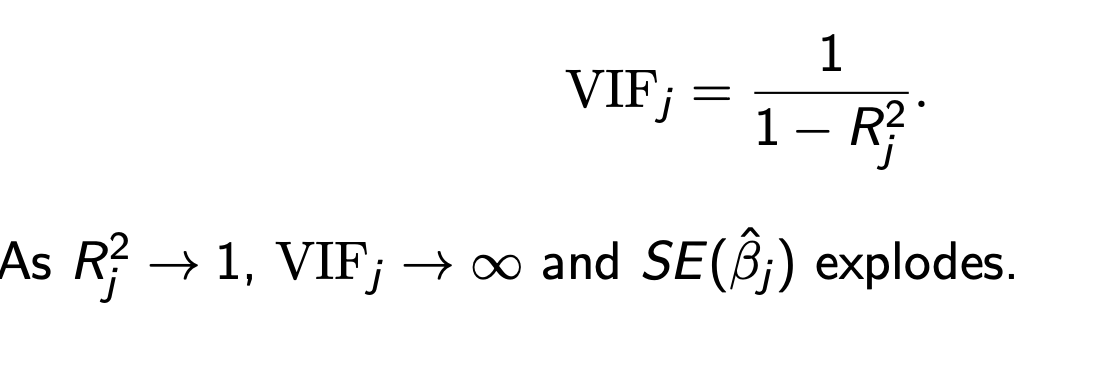
How to dieagnosse MC

• pairwise corr among regressors

• scatterplots/corr heatmaps

• collect Rj²

• get VIF

• VIF GREATER THAN 10 IS SEVERE

What are sources of MC

Dummy var trap, deterministic identities, similar proxies, high order polynomials

source of MC: Dummy var trap

including all factor of dummies and an intercept - remove and use one cat as ref

source of MC: deterministic identities

vars are exact cobinations/sum to one paired with other vars

source of MC: too simiar proxies

add highly corr measures of same concept

source of MC: high order polynomials

x/x²/x³/x^4 can be highly corr with finite samples

helps to center xHo 

how to fix MC

simplify: drop redunant vars/combine proxies

Transform: center/standardize regressors

Theory first: justify variables by model want to test

Prediciton: regularization methods

Heterskedasticity vs homoskedastity

variance of u given x is constant (sigma²) over i

HETERO it RELIES ON sigma² of i - VARIES ON i/Xi

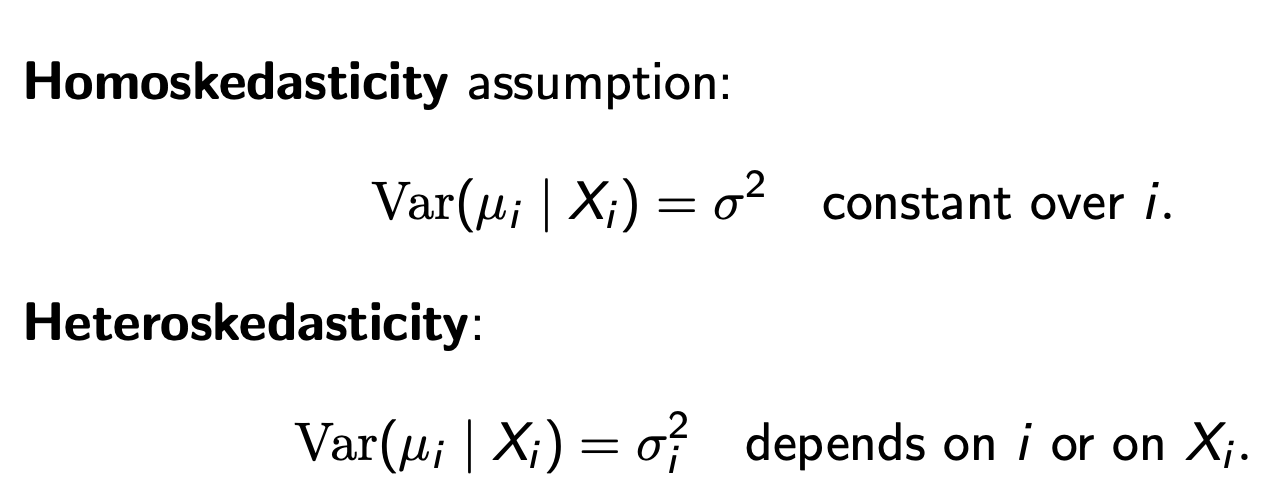
Effects of heteroskedasticy on OLS

OLS coeffs are UBIASED AND CONSISTENT

OLS SE are INVALID

• therefore t/F tests based on SE are invalid

Breush Pagan Test

Tests whether error variance depends on regressors

Ho: homoskedasticity

test stat = nR² (follows X²m distribution ) (m = number of regressors in aux)

Breush Pagan test steps

1. Estimate OLS, get resid

2. regress squared resid on variables

3. compute nR² from aux

White Test

Ho: constant variance of errors, model is correctly specified

regresses resid on X but also on X² and interactions

null: nR² follows X²q (q = nuber of aux regressors

NED LARGE N (aux reg is big)

can use subset

heteroskedasticity robust standard error

all diff obs have individual SE - use each squared resid in variance calc

SE robust > SE OLS (heteroskedasticity is present)

White’s (1980) heteroskedasticity-consistent estimator

each squared residual used directly

Weigted Least squares

impproves coefficients 

• get ui from ols

• model squared resid as function of x

• run WLS using weight of w= 1/sigma²

  • may need to repea

When to use robust SEs?

misspecified variance

What to do for heteroskedasticity

• plot resid against fitted vals

• use BP/white test to diagnose

• report hetero-robust SE

• consider WLS if variance pattern present

What are main sources of model misspecification?

• wrong regressors

• measurement errors

• wrong functional forms

Misspecification: Wrong regressors/omitted vars

estimated coeff = B1 + b2 (cov x1*x2 / var x1)

omitting pos cor regressive increases biases in corr regressors

Misspecification: Wrong regressors/endogeneity

regressor corr w error (covariance between regressor/resid ≠ 0)

FAILS ZERO MEAN COND

• could be from omitted vars

• simultaneity/reverse causlaity

• measurement error in x

CAUSES BIASED/INCONSISTENT OLS

fix w better design/controls/instrumental vars

Misspecification: Wrong regressors/irrel vars

B1 remains unbiased

variance of B1 increases (R2 increases bc extra regressors)

lowers power of tests/wide CI

Misspecification: Wrong form/curvature

what is it, what are effects, how to diagnose?

conditional mean nonlenear, model estimated only in x not x²

OLS BIASED AND INCONSISTENT

diagnosis:

• resid vs fitted values = systematic pattterns

• scatter of y/x reveal curve

fix by adding x², poly, or transform

Y = b ln x

<> y for 1% <> in X

ln y = bx

Percent <> in y for 1 unit <> in x

ln y = bln x

b = elasticity, partial deriv of y wrt x 

misspecifications; functional form: interactions

effect of x depends on x2

omitting interaction = misspec and biased slope on x1/x2

expected val of y given x wrt x1 = b1 + b3x2

Ramsey RESET

form check

if functional form correct higher order functions of fitted vals should not add explanatory power

1. estimate baseline and get y^

2. reestimate w extra powers of y^², y^³

3. use f test for joint sig of added terms

Ho: no nonlinear terms or interactions

general check (doesnt identify exact form needed)

Endogeniety problem 

mean value of residuals  is not zero 

biased/inconsistent cov

from reverse causality, omitted vars, measurement error

Why does OLS fail with simultaneity

• regressors are not exogenous (corr with error term)

Endogenous

jointly determined within system
ex. price/quantity within a market

Exogenous

proxy for ability/regressor

ex) weather and income

Proxy variable

proxy for ability/regressor that is included inregressionIn

Instrumental variable

z, instrument that affects x (helps predict) but is uncorrelated with our dependent variable (but only trhough x not directly)

helps us to isolate exogenous variation in endogenous regressor x

ex. weather shocks affect regressor agricultural supply but X consumer demand directly

What are conditions for a valid instrument (2)?

Revelance: must be corr with x (cov and must have non-zero coeff in auxilariy)

Exogeniety (inclusion restriction)

Z affects y only thorugh X (not directly or through omitted variables

Weak relevance

fails relevance

Strong invalid instrument

fails exogeniety

How to test relevance 

1st stage regression

if x = pi0 + pi Z + V and pi ≠ 0, then z is relevant (good)

2nd stage: estimate structural model by LS (replace endo reg 2 fitted xx^ from first stage)

How to test exogeniety?

cannot, U is unobserved must justify using economic reasoning

F stat

Ho: instruments are irrelevant (pi = 0)

F STAT > 10 is strong instrument

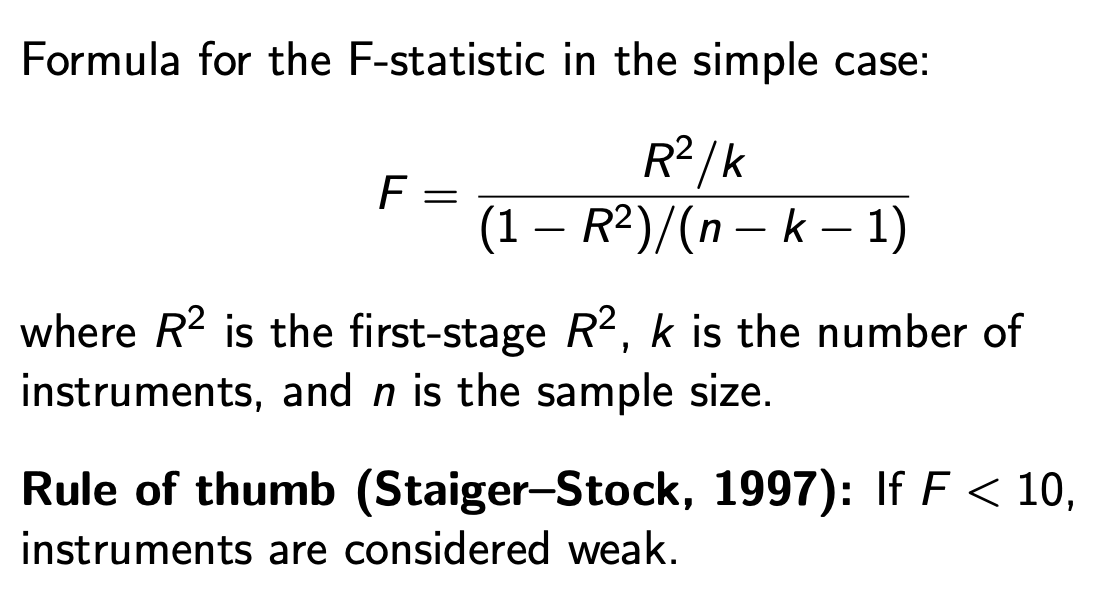
What is the coefficeint of the IV estimator? 

B^ iv = cov(z,y) / cov(z,x)

if x is its own instrument you get cov(x,y)/var(x) = regular OLS

2SLS

Two stage least squares estimates

CAN DIFFER SIGNIFICANTLY FROM STANDARD OLS

x^ = purged version of X

removes endogenous part of x before running wnd stage reg

When/why to use 2SLS

if regressors are exogenous

if not OLS is unbiased and more efficient than 2SLS

How to compare OLS/2SLS? 

Hausman (Durbin-Wu-Hausman) test 

if both consistent (regressor exogenous) they should be close

if only 2SLS consistent (regressor endogenous) they differ systematically 

Hausman Test Interp/Steps

Ho: OLS is okay (exogenous)

Ha: OLS is inconsistent (endogenous)

Steps:

• Estimate model by OSL/2SLS

• Compute diff bt coeff vec

• test whether this diff is stat sig

What are main objectives when using time series?

dynamic modeling, forecasting

(understand structure/response to shocks and accurate predictions)

Persistence

Lasting effects of shocks

Financial returns stylized facts

• weak/no autocorr

• voliatity clusters (lg <> followed by lg <> and VV)

• asymmetric volatality (neg shocks inc volatility more than + shocks)

Beta in time series

CAPTURES SYSTEMATIC RISK (that X be diversified away)

B measures sensitivity of stocks return to movt in overall market

>> Response of asset returns to market returns

slope of regression of Ri onto Rm

trend

Spurious regression

if Xt1/xt2  affect yt, ommiting t can bias regression

2 related variables trend over time 

including a B3t3 allows yt to have its own effect on trend after controlling for x1t/x2t

unrellated variables may trend togethre over time —> corr ≠ causation 

multiplicative decomposition

Yt = Tt * Ct * St * ut *

take logs to get into additive form: ln(y) = ln(t) + ln(C)

Methods of removing seasonality

• remove dummy variables

• mean average smoothing

Remove seasonality with dummy variables 

regress yt on szl dummy variables 

D = 1 if obs in that time period

et = resid 

* Note that m = 2, do not do all otherwise perfect MC

FITTED COMPONENT CAPTURES SZL

RESIDUAL = DE-SZNL SERIES (can always add Y back in)

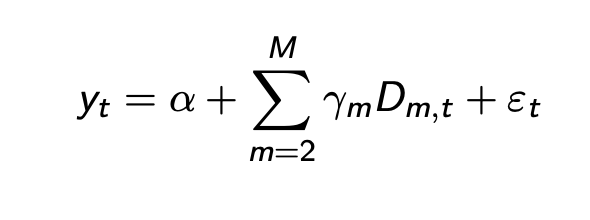
Moving average smothing 

larger q = smoother trend 

estimated trend is avg of q obs

centered moving avg

uses past/future obs

non-centered moving avg

only present/past obs

Trend-Cycle decomp

long/med movt

often estimated together bc difficult to seperate

How to sep trend-cycle?

HP filter

HP filter

Hodrick-Prescott filter: separates long-term comp from short term cyclical fluctuations (Ct = yt - Tt)

Term 1: ensures trend Tt follows yt closely 

Term 2: penalizes <> in slope of T to ensure smoothness 

Standard smoothing parameter: lamda = 1600, … 

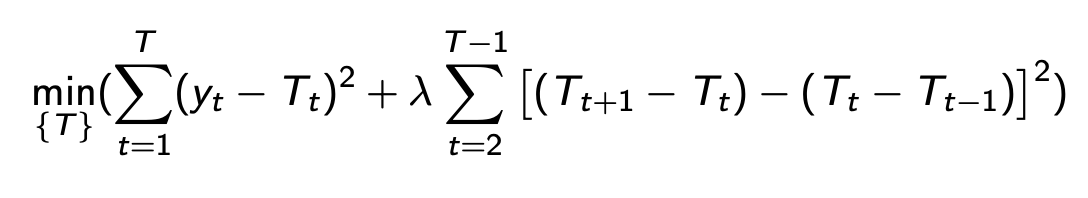
X-13ARIMA-SEATS

method of szn adjustment in nat stat offices

X13ARIMA: TS decomp based on moving averages/ARIMA

SEATS: extracts sznl trend/irregular

>> getrs rid of recurring szn patterns, estimate underlying trend/cylical movt, improve comparability across timeW

White Noise

ut ~ (0, sigma²)

no autocorr

Random walk

summed sequence of random shocks/white noise terms 

yt = yt-1 + ut

yt = y0 + u1 + … ut

ex) stock prices