Beam bending and shear force, and second moments (8a)

What is a bending beam, and what assumptions apply to the beams discussed here?

• A bending beam is a slender structural member, often horizontal, subjected to loads in one plane that act perpendicular to the beam axis.

• The beams considered here are prismatic beams (constant cross-section).

• Analysis assumes the beam operates in the linear elastic region, with small deflections and small strains.

What are the two types of beams considered?

• Simply Supported Beam:

  • Supported at both ends by knife-edge simple supports.

  • One support is often shown on rollers to indicate no longitudinal constraint.

• Cantilever Beam:

  • Supported at one end only by a built-in (fixed) support.

What happens inside a beam when it bends under load?

• When a beam bends, it develops internal forces and internal bending moments at every point along its span.

• For a simply supported beam with a point load W at mid-span, these internal forces and moments vary along the beam to maintain equilibrium and resist the applied load.

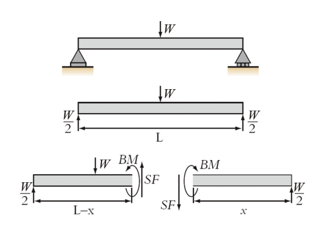
How do supports and internal forces behave in a simply supported beam with a central point load?

• The simple supports produce vertical reaction forces, each equal to W/2 due to symmetry.

• By sectioning the beam and drawing free-body diagrams of either side, equilibrium requires that an internal shear force and an internal bending moment exist at the cross-section.

• These internal actions ensure the beam remains in static equilibrium under the load.

Why does a shear force exist inside a simply supported beam with a central point load?

• In the right-hand section of the beam, a shear force (SF) must act on the internal cut face to balance the vertical reaction force W/2W/2W/2.

• This internal shear force acts to shear the cross-sectional plane (perpendicular to the beam axis) and is required to maintain vertical force equilibrium.

Why does a bending moment exist inside a simply supported beam?

• A bending moment (BM) must exist at the internal cross-section to satisfy rotational equilibrium.

• It counteracts the combined effect of the reaction force W/2W/2W/2 and the shear force (SF), preventing the beam from rotating.

• This internal moment acts to bend the beam’s cross-section and is present at every point along the beam where bending occurs.

What internal forces act on the left-hand section of a simply supported beam?

• The left-hand section must also have an internal shear force and bending moment on its internal face to maintain equilibrium.

• These internal actions are equal in magnitude but opposite in direction to the shear force and bending moment on the right-hand face of the same cross-section.

Why must we determine how shear force and bending moment vary along a beam?

• exist at every section along the beam, but their magnitudes vary depending on the location.

• Understanding these variations is essential because they determine the bending stress distribution within the beam.

• Accurate diagrams are therefore critical for structural analysis and design.

Why is a sign convention needed before determining shear force and bending moment distributions?

• A sign convention must be defined for both shear force and bending moment to ensure that calculations are consistent and unambiguous.

• It establishes a clear framework for identifying positive and negative shear forces and bending moments when analysing their distribution along the beam.

How do we analyse a beam section under a Uniformly Distributed Load (UDL)?

• When analysing a UDL, we cut the beam at a chosen section and treat the cut portion as a free body.

• This approach is similar to the point load case, where the left-hand section was used as the free body.

• The distributed load over the cut section is replaced by its equivalent resultant force, acting at the centroid of the loaded length.

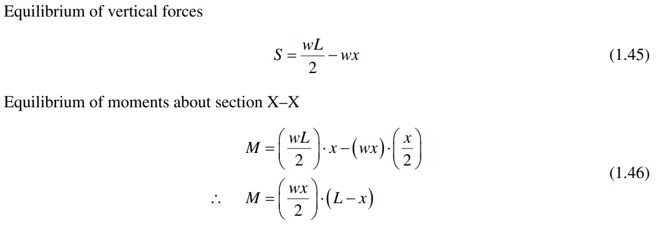
How are shear force and bending moment related in a beam under a UDL?

• For a beam with a uniformly distributed load (UDL) w, consider a small element of length dx.

• Over this distance:

  • The shear force changes from S to S + dS.

  • The bending moment changes from M to M + dM.

• Taking moments about the right-hand end (point A) of this small element and applying equilibrium leads to the relationship between shear force and bending moment.

• This results in the fundamental differential equation:
  dM/dx = S.

What is the key relationship between shear force and the bending moment curve?

• The shear force at any point on a beam equals the negative slope of the bending moment curve.

• Mathematically:
  S(x) = dM/dx.

How do different loading types affect shear force and bending moment?

• Point Load:

  • Produces constant shear between loads.

  • Produces a linear (straight-line) bending moment between loads.

• Uniformly Distributed Load (UDL):

  • Produces linear (sloping) shear.

  • Produces a parabolic bending moment.

What do shear force and bending moment diagrams show, and why are they important?

• Shear Force (SF) and Bending Moment (BM) diagrams show how the internal shear forces and internal bending moments vary along the beam.

• They are essential for analysing stresses, determining critical sections, and ensuring safe structural design.