Handout 2: General addition & multiplication rule, [B|A]

Week 2

When do we use the general addition rule?

If events A and B are disjoint, we use simple addition

If events A and B are not disjoint, we use the general addition rule to not double count!

What is the general addition rule?

P(A or B) = P(A) + P(B) - P(A and B)

What is conditional probability?

This presumes that an event has occurred

• ex. if you have lung cancer, assume you were a smoker

How do you find the probability of event B given event A?

P[B|A] = P[A and B] / P[A]

• always divide by the probability of the event given! (B, GIVEN A)

• ex. finding the probability of being in 1st class and surviving (not disjoint)

When would you use the general multiplication rule?

When events A and B are independent, we can use the multiplication rule

• BUT the general multiplication rule is used when events A and B are dependent

What is the general multiplication rule?

P[A and B] = P[A] x P[B | A]

P[B and A] = P[A] x P[A | B]

What is interdependence?

• If events A does not help you find the probability of B, they are independent

• Disjoint events are dependent (knowing something about 1 reveals info about the other)

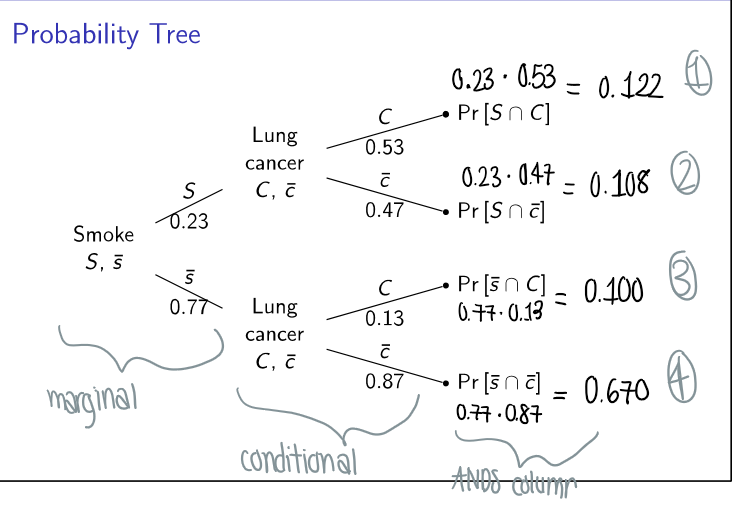
What is a possibility tree?

A different representation of a contingency table