Fracture Mechanics

1. Assess the question, 2. Attempt question on Paper/ Chalkboard, 3. Look at answers & assess level of knowledge

Find Stress Amplitude ?

1. Endurance limit given

2. Tensile Strength = UTS, needed for Calculation

3. Determine which model to use to evaluate fatigue life based on material properties and loading conditions: Soderberg (based on Yield Stress) , Goodman (based on UTS) & Gerber (non-linear & UTS squared)

4. Using Goodman model as Yield Stress isn’t given & linear.

5. Rearrange equations for Stress Amplitude

🧠 What are the differences between plane strain fracture toughness and plane stress fracture toughness?
Hint: Think about thickness, crack-tip constraints, and toughness values.

• Plane Strain Fracture Toughness (KIcK_{Ic}KIc​):

  • Occurs in thick specimens.

  • Out-of-plane deformation is restrained.

  • Offers smaller plastic zone

  • Used for conservative (safe) design.

• Plane Stress Fracture Toughness:

  • Occurs in thin specimens.

  • Material can deform in all directions.

  • Less constraint → higher apparent toughness.

• Comparison:

  • K IC, plane strain < K plane stress

  • Plane strain gives a worst-case estimate of material fracture resistance.

🔧 A SENB specimen with B=12 mm,a=12.2 mmB = 12 \text{ mm}, a = 12.2 \text{ mm}B=12 mm,a=12.2 mm, pop-in at 10.2 kN, max load 11.7 kN. What is KQ​?

1. Force at Crack Pop (not Max Load !!!)

2. Find f(a/w)

3. Input into KQ equation

4. VALIDITY CHECKS: (gives most of marks)

5. Pmax / PQ < 1.1

6. Check smallest parameter & complete validity check

🔬 What is the purpose of plane strain fracture toughness testing (e.g. SENB and CT specimens)?

Measure the material’s resistance to crack growth in the most conservative (least tough) condition: plane strain. Due to smallest plastic zone .

🔍 How is crack initiation (PQ) identified in SENB/CT tests?
Hint: 3 types of failure, Pmax rules.

To find PQ:

1. Type I: PQ = PS (load where deviation starts)

2. Type II: PQ = Highest load before PS (pop-in)

3. Type III: PQ = Pmax (brittle fracture)

Check validity:

• Pmax / PQ ​< 1.10

• If not, PQ invalid → test fails

📉 A steel plate with a 20 cm crack is subjected to 65 MPa stress. How do you calculate the safety factor using the R6 diagram?

1. Draw a diagram of the component, determine what type of crack it is (e.g. Centre crack)

2. Determine b , distance between the crack & the edge of the sample (in this case b is on either sides of the crack & do not simplify the given value for 2a)

3. b = W - 2a / 2 , in order to get one value for b this only applies for centre cracks

4. Now find Pc, collapse load

5. Find Pi, applied load = Applied Stress x Width x Thickness

6. Lr = Pi / Pc (Applied / Collapse Load)

7. Find C, Stress Intensity Factor for Centre Crack

8. Find Ki, (Applied) using Paris Law Eqn.

9. Use KC, (Fracture Toughness = Collapse) given in Equation

10. Kr = Ki / KC

11. Plot point (Lr, Kr) = (0.204, 0.396) on the R6 diagram and draw a line from origin to point B.
    Use the triangle rule:

    FL=OB/OA

(OA - the distance to the plotted points added up, OB - the distance to the projected values intercepted on the line added up.)

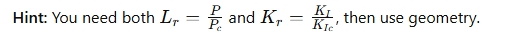
🔁 What happens to the safety factor if the crack doubles in length under cyclic loading from 0 to 65 MPa?

Redo Lr​ & Kr​ for crack length 40 cm.

🔍 A fracture toughness test on a CT specimen (B = 50 mm) gives varied crack lengths. PQ​=180 kN, Pmax​=190 kN, σy​=920 MPa. Is the result valid and what is the fracture toughness?

1. Highlight what test is being performed (E.g. Compact Tension Test)

2. Find parameters: W

3. Mean Crack Length, a (Is NOT based on the surface, as the surface is based on Plane Stress, whereas the interior is only under plane strain conditions.)

4. As Crack Pop, the Load , F is NOT based on the maximum load but is the LOAD AT the crack pop !

5. Find a/w & shape function - f(a/w) for Compact Tension Test

6. Calculate KQ value

7. VALIDITY TESTS:

8. Pmax/PQ < 1.1

9. Find smallest parameter (e.g. B)

10. Next calculate validity for multiple parameters of a. (BOTH AT THE SURFACE & THE CENTRE)

11. For the centre, keep a1 consistent for the first value of the numerator & the numerator, use first equation for the centre

12. For the surface, keep a1 consistent from the previous, just change the second value in the numerator & use the second equation for the surface.

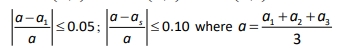
📈 Estimate the fatigue lifetime of a plate using:

1. Find out what type of crack = Edge or Centre

2. Ensure: a, initial crack length is correct value & calculate C

3. Rearrange & Find Critical Crack Length, using Paris Law Equation: KIC = C*max stress sqrt (pi *ac)

4. Now Find n:

5. Input delta K except for a, rearrange of dn

6. Integrate both sides & take out constant term

7. Apply limit for a (i.e. ac & ai)

8. Finis

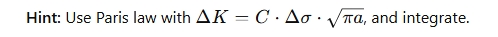
If the plate is subjected to periodic positive overloads how would this affect the calculated lifetime ?

• Initial effect: Crack grows faster due to spike in ΔK\Delta KΔK

• Afterward: Residual compressive stresses reduce crack growth rate

• Net effect: Retardation occurs → lifetime increases

📈 Estimate the fatigue lifetime of a plate using:

1. Find out what type of crack = Edge or Centre

2. Ensure: a, initial crack length is correct value & calculate C

3. Rearrange & Find Critical Crack Length, using Paris Law Equation: KIC = C*max stress sqrt (pi *ac)

4. Now Find n:

5. Input delta K except for a, rearrange of dn

6. Integrate both sides & take out constant term

7. Apply limit for a (i.e. ac & ai)

8. Finis

Sources of Error

Assumption of Constant Geometry Factor (C):

• We usually assume approx. C≈1, but in reality it can vary as the crack grows.

• Likely effect: Overestimate

Estimate the time to failure (in days).
Then state whether this estimate is likely to be an over- or under-estimate.