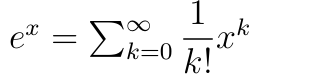Calc 2 exam final

sin²(ax)

(1 - cos(2*a*x)) / 2

cos²(a*x)

(1 + cos(2*a*x)) / 2

integral of sec(x)

ln|secx + tanx|

integral of tanx

-ln|cosx| or ln|secx|

root(a²-x²)

x=a * sin(theta) dont forget to multiply by dx

root(a²+x²)

x=a * tan(theta) dont forget to multiply by dx

root(x²-a²)

x = a * sec(theta) dont forget to multiply by dx

sin(2 * theta)

2cos(theta) * sin(theta)

Arc length formula

Integral of root(1 + (f’(x))²)

Degree of numerator equal to or greater than denominator

Use polynomial long division

derivative of arcsin(x)

1/(root(1-x²))

derivative of arccos(x)

-1/(root(1-x²))

derivative of arctan(x)

1(1+x²)

derivative of cot(x)

-1/(1+x²)

derivative of arcsec(x)

1/(|x|*root(x²-1))

derivative of arccos(x)

-1/(|x|*root(x²-1))

lim(x→oo or -oo) of arcsin(x) and arccos(x)

DNE

lim(x→oo) of arctan(x)

pi/2

lim(x→ -oo) of arctan(x)

-pi/2

lim(x→oo) arccot(x)

0

lim(x→ -oo) arccot(x)

pi

lim(x→oo or -oo) arcsec(x)

pi/2

lim(x→oo) arccsc(x)

0

lim(x→ -oo) arccsc(x)

pi

r = a + b * sin(theta)

limacon of original circle

petals

constant multiplying theta, if the constant is even then there are two times the constant amount of petals

Cos petals are centered on the axis, and sins petals are rotated by pi/(2 * the constant multiplying theta)

each petal that isn’t there as a result of the even coefficient rule is created as if it was generated on its original axis (IE 3cos(4 theta) has 8 petals, all petals lying on the axis’ are affected by the +b and coefficient of the functions effects on the x and y axis as if it was the original petal, and then its rotated, the extra petals from the even rule have the x intercept of the function coefficient minus the shift constant, and y axis for sin)

x²+y²=r² properties

centered at (zero(s) of x, zero(s) of y) with radius r

1-cos(theta)

2sin²(theta / 2)

tangent line is horizontal when

derivative is zero

Quadratic formula

Remember, x can be anything, it can be (x-1) or even cos(x) or cos(θ))

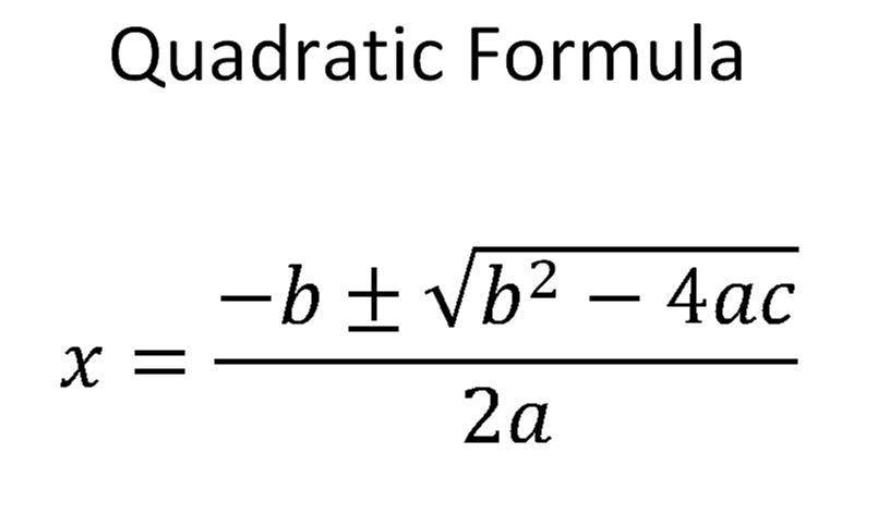
Z

a+bi and r(cosθ + isinθ)

a

rcosθ

b

rsinθ

tanθ

b / a

z_k

r * e^{(i * θ_k)}

θ_k

2kπ/n (where k is 1 less than the solution number we’re on and n is the total number of solutions)

z (for polar complex solutions)

r*e^iθ

r in complex solutions (z_k)

value when Z is isolated

z (for polar complex solutions)

plug θ_k into the r(cosθ + isinθ)

Area

magnitude of cross product

Shell Method

2π * integral from a to b of x or y times h₂ - h₁

Washer method

π * the integral from a to b of R² - r²

Surface Area integral

integral from a to b of 2π * f(x) times square root of 1 + f’(x)²

cos(2x)

1-2sin²(x)

sin(u)

behaves like u for small u values

cos(u)

behaves like (-1)^k for large u (doesn’t qualify for AST)

e^x summation formula