Discrete Mathematics

What are tautologies?

A tautology is a statement in logic that is always true, no matter what the truth values of its components are.

What are the domination laws?

x∨1=1 and x∧0=0 for ANY x

How do you prove a “if and only if” statement?

If a then b AND if b then a.

What is a quotient of a set?

A quotient of a set (sometimes called a quotient set) is what you get when you take a set and group together elements that are equivalent under some equivalence relation.

What does A x A mean?

It literally lists every possible pair of elements in A.

R∪R^−1=A×A - what does this express?

• It expresses a linear partial order

What does it mean for 2 numbers to be congruent modulo m?

They leave the same remainder when divided by m.

How is set builder notation read?

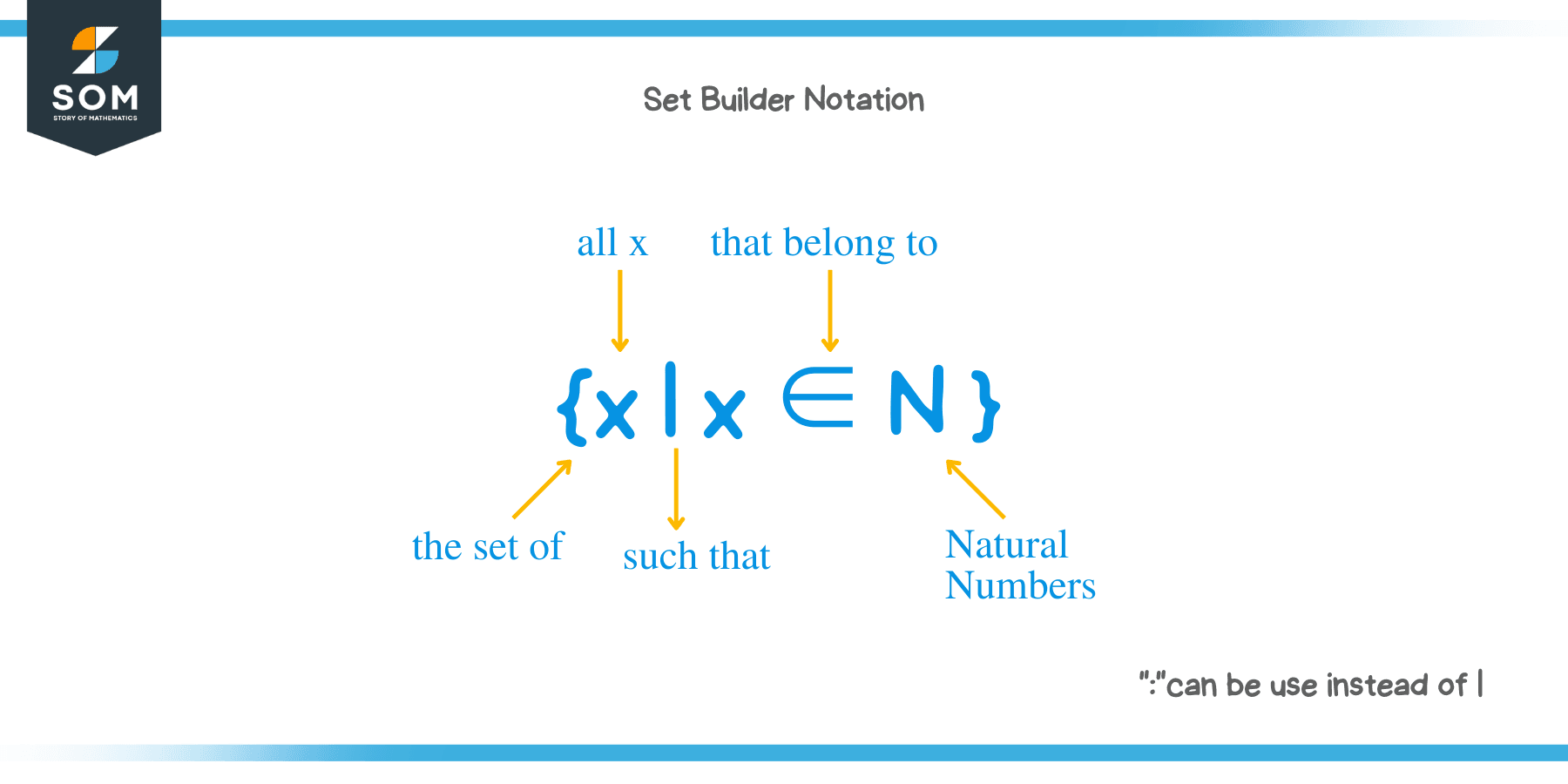
What is the definition of a quotient in maths?

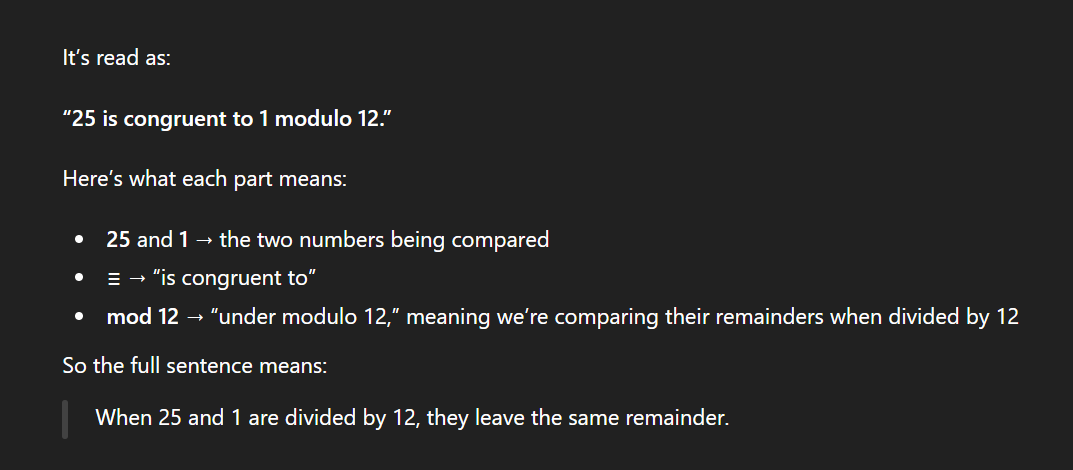
What does 25 ≡ 1 mod 12  mean?

• Divide 25 by 12 → 25÷12 = 2 remainder 1

• Divide 1 by 12 → 1÷12 = 0 remainder 1

What is Peano arithmetic?

What is the definition of + ?

What are the semantic rules of Boolean Formulae?

What are the rules for Disjunctive Normal Form (DNF) ?

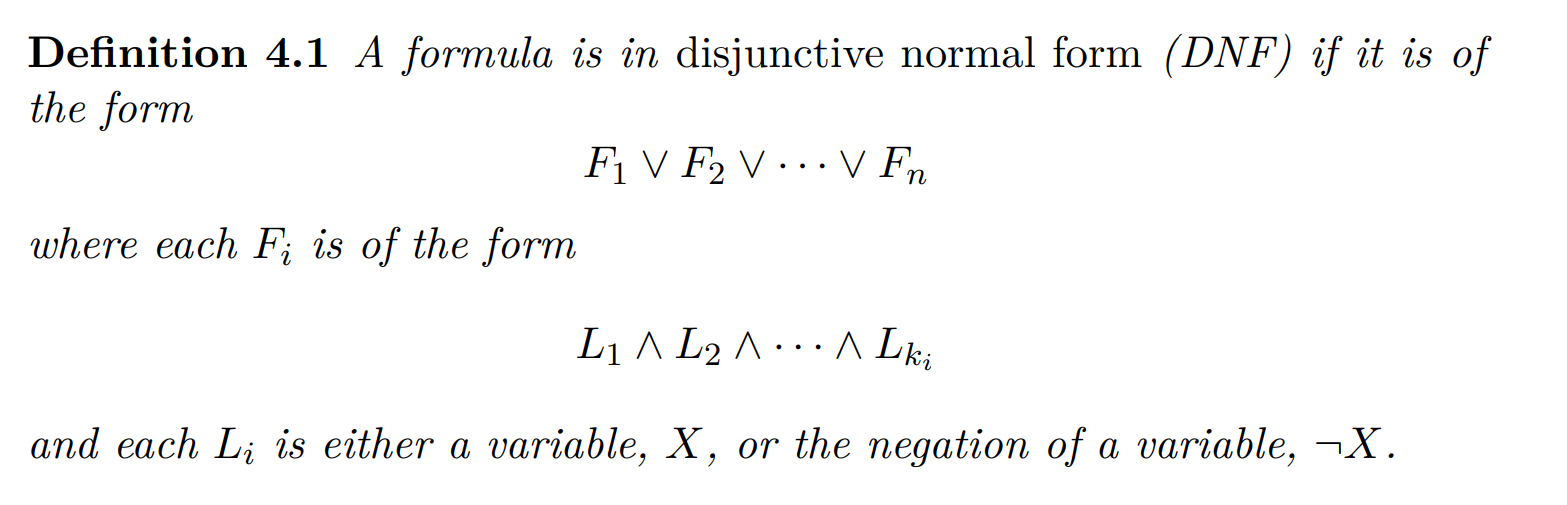
What are the rules for Conjunctive Normal Form (CNF) ?

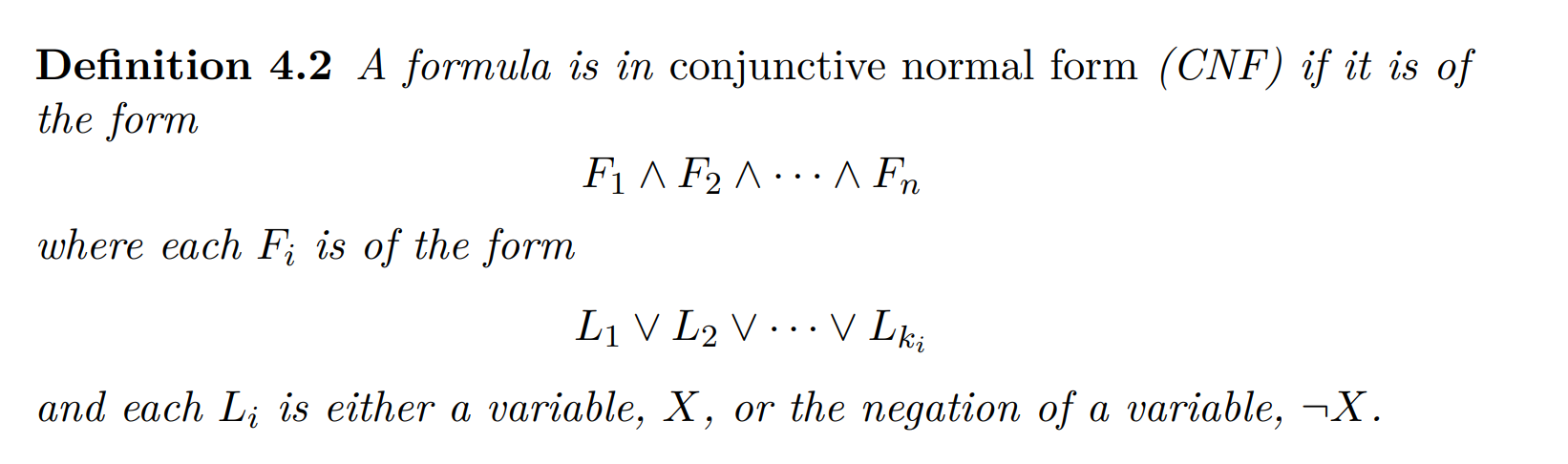
F = F1 ∧ F2 , is it true that F1 & F2 have fewer symbols than F

YES! Because the symbols in F1 & F2 are also counted in F!

What is the meaning of “↔”

Equal to

How does course-of-values induction work?

((X→Y)∧(¬X→Y))→Y - is this always true?

Yes, since x → y is only false when y is false, which is not the case when x is either true or false here.

When is a relation antisymmetric?

A relation R on a set A is antisymmetric if, whenever a R b and b R a, it is the case that a = b.

What is the definition of R^−1

When are 2 functions equal?

If they give the same output on every input. This is the same as saying that they are equal as sets of pairs, because every input value belongs to exactly one pair by definition of function.

What does “R is a relation on A” mean?

Both elements in each pair come from the same set A

For a finite set size, and 2 functions that are both injective, what must the sizes of A and B be?

∣A∣ ≤ ∣B∣, since injective function is a 1-1 function, but there can be elements in B that are not reached. However, every element in A must distinctly map to ONLY 1 element in B.

f:A→B (What exactly does it mean?)

• A is the domain — the set of all possible inputs for the function f.

• B is the codomain — the set that contains all possible outputs of f.

f is a function that takes elements from the set A and sends them to elements in the set B.

What is commutative?

The order of the operation doesn’t matter — you get the same result either way.

What does “id” mean?

What does R^−1⊆ R mean?

“every element of R−1 is also in R.”

What does ⟺ mean?

If and only if

What is a reflexive relation?

“If I put the same number in both places, does the relation still hold?”

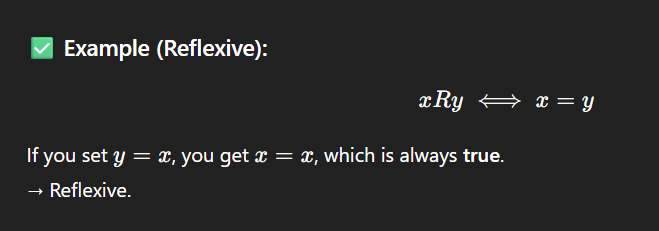
What is meant by parity?

Parity refers to whether an integer is even or odd.

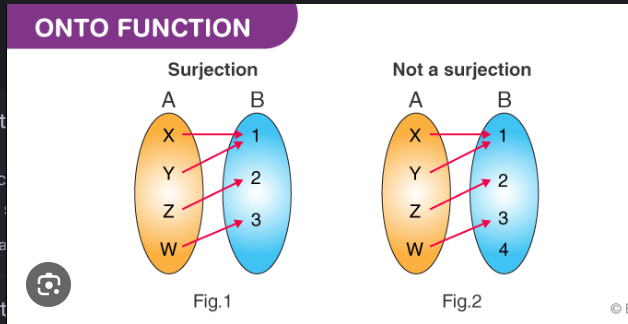
What are surjective functions?

“Everything is reached in B" (CAN but does not have to have more than one A going to the same B)

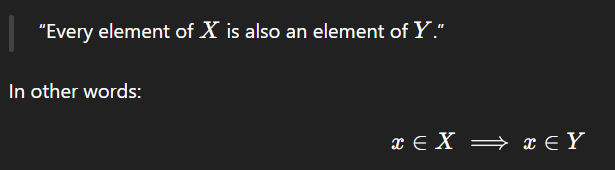
What does this mean: X⊆Y

What are equinumerous sets?

A is the same size as B if there is a bijection between A and B

What does PN mean? (Power set)

The set of sets of naturals (A powerset is the set of all possible subsets of a given set, including the empty set and the set itself.)

What are injective functions?

1-1

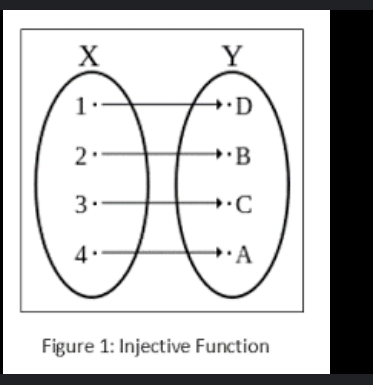
What are bijective functions?

Both surjective and injective functions

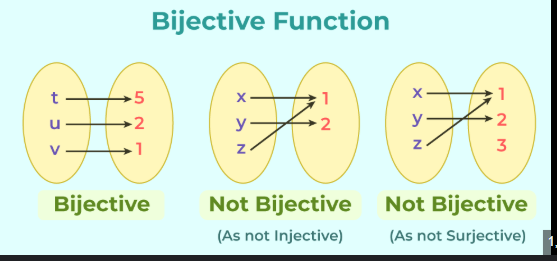
What are the 2 conditions for an inverse relation to be a function?

What is a cartesian product?

Given two sets A and B, the Cartesian product A×B is the set of all ordered pairs where the first element comes from A and the second element comes from B

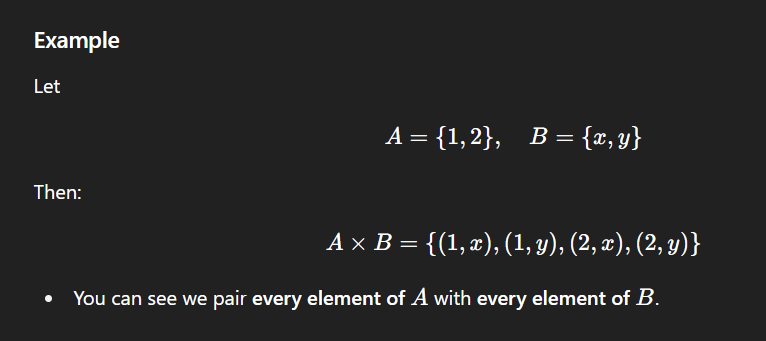
What is a reflective binary relation between a set?

A binary relation R on a set A is reflexive if a R a for every a ∈ A.

(every element of the set is related to itself)

What is R in a R b?

R is itself a set that That means R is a subset of the Cartesian product of two sets A and B.

When is a binary relation transitive?

If a is related to b, and b is related to c,
then a must also be related to c.

What is a proposition?

A statement that is either true or false, BUT NOT BOTH!

What are the distributive laws?

Can you use implication in de Morgan law?

No, it must be only with AND and OR

Write in logical notation. (don’t forget div(x,y) meaning)

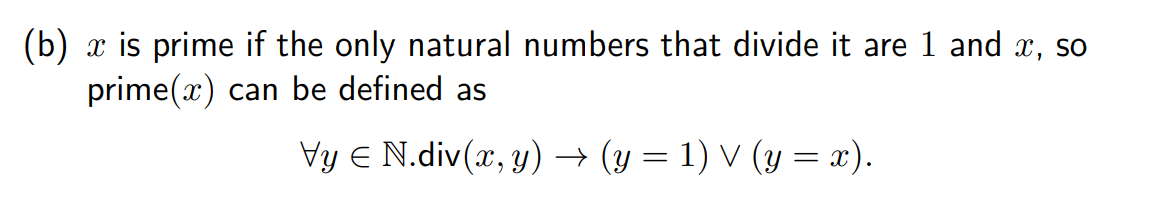
How to read implication?

What does the full stop mean in set notation?

Such that

What does disjoint mean?

Two sets X and Y are called disjoint if X ∩ Y = ∅.

(A∨B)∧(C∨D) ≡ ? (using distributive laws?)

(A∧C)∨(A∧D)∨(B∧C)∨(B∧D).

What is the law of excluded middle.

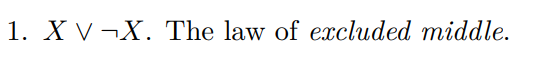
How can X ∨ ¬X be expressed with implication?

(X → Y )

What is a literal?

A propersitin variable (X,Y)

What are the 2 rules for a set?

A set is determined completely by its elements: all that matters is whether an element is in a set or not.

A set doesn’t keep its elements in any particular order, and an element cannot appear more than once in a set. (writing an element more than once does not change the set.)

What is a predicate?

A proposition with a variable (x is a number)

What is a proposition?

a statement that is either true or false, but not both.

What are the absorption laws?

X ∨ ( X ∧ Y) = X

X ∧ (X ∨ Y) = X

What are the distributivity laws?

Distributivity: x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z)

x ∧ (y ∨ z) = (x ∧ y) ∨ (x ∧ z).

What are the 5 axioms that must hold for something to be Boolean algebra

Associativity

Absorption

Distributivity

Commutativity

Complements

Is ∅ (the empty set) in every possible set?

YES!

How can you work out how many elements are in a power element P(A)

2^n where n = number of elements in A

{x | (x ∈ A) ∨ (x ∈ B)}. What does this mean?

The set of all elements x such that the condition is true.

What is the existential quantifier symbol?

∃

y∣x  - what does this mean?

When we say “y divides x” (written y∣xy \mid xy∣x), we mean:

x is a multiple of y, or equivalently, x can be written as y times some integer.

What does “:” mean?

means “is defined as” or “means that.”

Are quantifiers commutative?

No, only operations.