Chapter 10: Rotational Kinematics & Energy

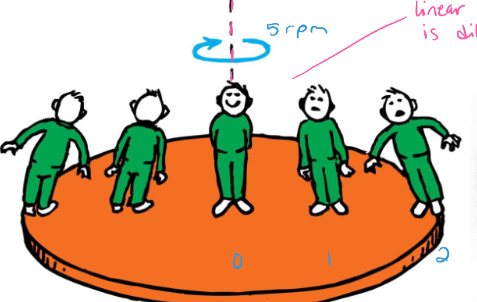
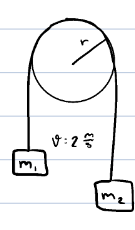
How do the rotational/angular speeds of each person compare?

• They all have the same rotational speeds

• Same rpm regardless of their position on the rotating system

• same ω

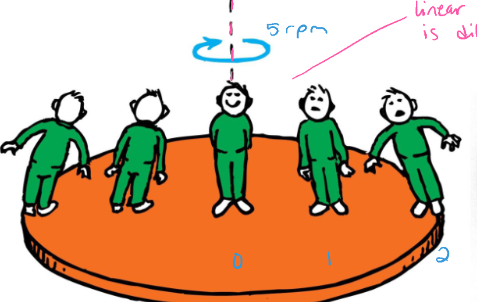
How do the linear speeds of each person compare?

• The person farthest from the axis of rotation has the highest linear speed

• linear speed increases with distance from the center of rotation

• v = ωr

  • ω is the same, radius increases → v increases

The top of a bike wheel…

• rotates 2x faster than the bottom

• top of wheel rotating forward, whole bike moving forward (botom of wheel moving backward)

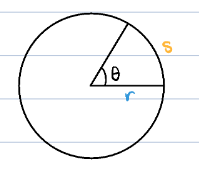
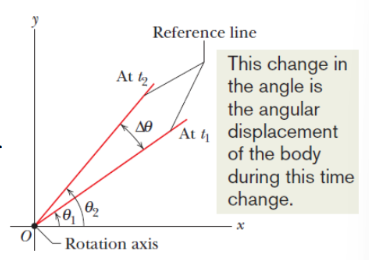
Angular Position

• θ = s/r

• r = radius: distance from rotational axis

• s = arc length

• θ in radians

In angular position, the reference line is _______ to the rotational axis.

perpendicular

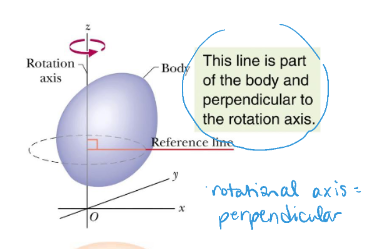
Angular Displacement

• If a body rotates about the rotation axis (changes angular position of reference line from θ₁ to θ ₂ ) the body undergoes angular displacement

• Δθ = θ₂ - θ₁

• in the counterclockwise direction = positive

• in the clockwise direction = negative

Angular Velocity

• how fast something is rotating

• how fast the angle is changing in time

• ω = Δθ/Δt

Rolling = ?

• translation (linear) + rotation

• K_roll = K_t + K_r

• K_roll = ½ mv² + ½ Iω²

2600 rev/min is equivalent to how many rad/sec?

(2600 rev/min)(1 min/60 s)(2pi rad/1 rev) = 273 rad/s

Angular Acceleration

• if the angular velocity is not constant → there is angular acceleration

• how fast the angular velocity is changing

  • speeding up: +, down: -, constant: 0

• α = Δω/Δt in rad/s²

If angular velocity (ω) is constant, what is angular acceleration?

• constant angular velocity = spinning/angle changing at the same speed all the time, not speeding up or slowing down

• there is no angular acceleration

• α= dω/dt = 0

Are angular quantities vectors?

Yes, angular quantities are vector quantities because they have both magnitude and direction.

A flywheel is initially rotating at 20 rad/s and has a constant angular acceleration. After 9.0 s it has rotated through 450 rad. Its angular acceleration is…?

• ω₀ = 20 rad/s

• t = 9.0 s

• angular displacement: θ = 450 rad

• angular acceleration = ?

• use kinematic equation:

  • θ = ω₀​t + ½ ​αt²

  • 450 rad = 20 rad/s*9.0 s + ½ (​α)(9.0)²

  • α = 6.67 rad/s²

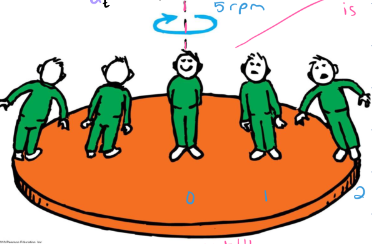
How would you find the person with the highest linear speed?

• v = ωr

• would convert 5 rpm to rad/s for angular speed

• then multiply each by their radius; person 2 will have highest linear speed

Radial Acceleration

• a_r = a_c = v²/r = ω²r

• equal to centripetal acceleration

• how hard the center-pulling force has to work to keep object moving in a circle

• points towards center

• arises due to change in direction

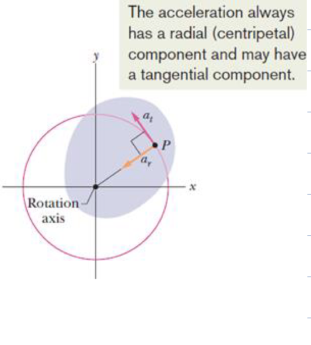
Tangential Acceleration

• a_t = αr

• a = sqrt( a_r² + a_t² )

• arises due to change in magnitude; points along direction of motion (tangent to the circle)

Tangential & Radial acceleration are…

perpendicular to each other

Calculate the linear speed due to the Earth’s rotation for a person at the equator of the Earth. The radius of the Earth is 6.40×10^6 m.

• v = ωr

• v = ?

• r = 6.40×10^6 m

• ω = ?

• ω = Δθ/Δt = 2π radians / 24 hours = (2π / 86400) radians per second

• v = (2π / 86400) rad/s * 6.40×10^6 m

• v = 465 m/s

Kinetic Energy of Rotation

• Treat a rotating rigid body as a collection of particles with different speeds and add up the kinetic energies of all particles to find total KE

• K = ½ m₁v₁² + ½ m₂v₂² + …

• K = ½ Iω²

  • radian measure where I is the moment of inertia of the body

  • ω is the same for all particles

Moment of Inertia

• A measure of an object's resistance to rotational motion

• dependent on the mass distribution relative to the axis of rotation

• I = ∑ m_ir_i²

  • m_i is mass and r_i is the distance from the axis

• linear: mass resists linear acceleration

• rotational: moment of inertia resists angular acceleration

A higher moment of inertia means…

• It is more difficult for the object to rotate

• inertia = resistance to changes in rotational motion

• due to greater mass distribution further from the axis

  • larger r

A lower moment of inertia means

• it is easier for the object to rotate

• inertia = resistance to changes in rotational motion

• due to less mass distribution closer to the axis

  • smaller r

Moment of Inertia Equation will…

vary based on the shape

A pulley with a radius of 3.0 cm and a rotational inertia of 4.5×10^-3 kg*m² is suspended from the ceiling. A rope passes over it with a 2.0-kg block attached to one end and a 4.0-kg block attached to the other. The rope does not slip on the pulley. When the velocity of the heavier block is 2.0 m/s, the total kinetic energy of the pulley and blocks is…

• r = 3.0 cm = 0.03 m

• I = 4.5×10^-3 kg*m²

• m₁ = 2.0 kg

• m₂ = 4.0 kg

• v = 2.0 m/s

1. Assign Linear vs. Rotational

• Linear = straight line = blocks

• Rotational = spinning about an axis = pulley

2. Connect Linear & Rotational

• Given v (linear), we need ω for pulley (rotational)

• v = ωr

• 2.0 m/s = ω(0.03 m) → ω = 66.7 rad/s

3. Find Total KE

• K = K₁ + K₂ + K_r

• K = ½ m₁v² + ½ m₂v² + ½ Iω²

• K = ½ (2.0 kg * 2.0² m/s) + ½ (4.0 kg x 2.0² m/s) + ½ (4.5×10^-3 kg x m²)((66.7 rad/s)²)

• K = 22 J

Rolling

• combination of translation of the center of mass and rotation of the rest of the object around that center

• rolling = linear/translational + rotational motion

Which wheel will win? A: rolling, B: sliding

• B: sliding will win

  • only translational motion, no rotation

  • All PE goes into linear kinetic energy

  • mgh = ½ mv²

• A: rolling will lose

  • has both translational and rotational motion

  • PE splits → some energy goes into spinning in addition to moving forward

  • mgh = ½ mv² + ½ Iω²

  • A has less linear velocity/speed in comparison

A rolling object has…

• 2 types of kinetic energy

• a rotational KE due to its rotation about its center of mass: ½ Iω²

• a translational KE due to translation of its center of mass: ½ mv²

A bowling ball is rolling without slipping at constant speed toward the pins on a lane. What percentage of the ball’s total KE is translational KE? Moment of inertia of a solid sphere is 2/5 MR².

• rolling without slipping: translational & rotational KE

• K_roll = K_t + K_r

• K_roll = ½ mv² + ½ Iω²

• K_roll = ½ mv² + ½ (2/5 mr²)(ω²)

• K_roll = ½ mv² + ½ (2/5 m(v²/ω²)(ω²))

• K_roll = ½ mv² + 1/5 mv²

  • factor out mv²

• K_roll = mv² * (1/2 + 1/5) = 7/10 mv²

• K_t = ½ mv²

• Fraction: K_t / K_roll = ½ / 7/10 = 71.4% translational KE

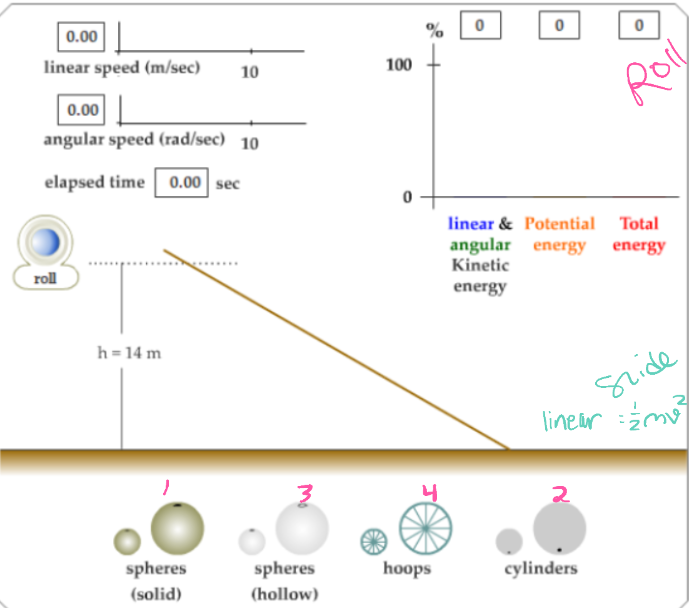
Which roll the fastest? Which slide the fastest?

• Roll: Solid sphere

  • greater mass moves faster due to greater mass distribution

  • when bigger fraction is rotational (2/3 vs 2/5 mr²) then the center moves slower and it will move slower

  • smaller I will move faster

• Slide: Linear, all the same

  • ½ mv²

  • all K_t when sliding, equivalent speed when from the same height

  • v = sqrt(2gh)

A solid sphere of mass 4.0 kg and radius 0.12 m starts from rest at the top of a ramp inclined 15 degrees and rolls to the bottom. The upper end of the ramp is 1.2 m higher than the lower end. What is the linear speed of the sphere when it reaches the bottom of the ramp? I = 2/5 MR² for a solid sphere and g = 9.8 m/s²

• m = 4.0 kg

• r = 0.12 m

• theta = 15 degrees

• h = 1.2 m

• I = 2/5 MR²

• g = 9.8 m/s²

• v = ?

• K_roll = K_t + K_r

• E_i = E_f

• (K_t + K_r + U_g)_i = (K_t + K_r + U_g)_f

  • K_t & K_r are initially = 0 because the sphere is at rest

  • U_g final is = 0 because the sphere will not have any more PE

• U_gi = ½ mv² + ½ Iω²

• U_gi = ½ mv² + ½ (2/5 mr²)(ω²)

• U_gi = ½ mv² + ½ (2/5 m(v²/ω²)(ω²))

• U_gi = ½ mv² + 1/5 mv²

  • factor out mv²

• U_gi = mv² * (1/2 + 1/5) = 7/10 mv²

• mgh = 7/10 mv²

  • m cancels

• (9.8 m/s)(1.2 m) = 7/10 v²

• v = 4.1 m/s