HCS 202 Exam 2

Purpose of hypothesis testing

Determine whether there is sufficicent evidence to make a sound scientific conclusion

what does a single sample t test compare

a sample mean to a population mean when the population standard deviation is unknown

what is required for a single sample t test

sample mean, sample standard deviation, and population mean

statistical assumptions

Characteristics about the data that need to be met before performing selected types of inferential statistics.

4 common assumptions

independence of data, appropriate measurement variables, normality of distributions, homogeneity of variance

independence of data

no two observations are related in a dataset (not robust)

appropriate measurement variables

the variables of interest must be measured on the appropriate scale (not robust)

normality of distributions

The distribution of sample means for each condition must have a normal shape (robust if sample size is over 30/large)

homogeneity of variance

standard deviations from the sample and population are similar (robust)

Non-robust assumptions

must be met in order to proceed

robust assumptions

assumptions can be violated to some degree and still continue with test

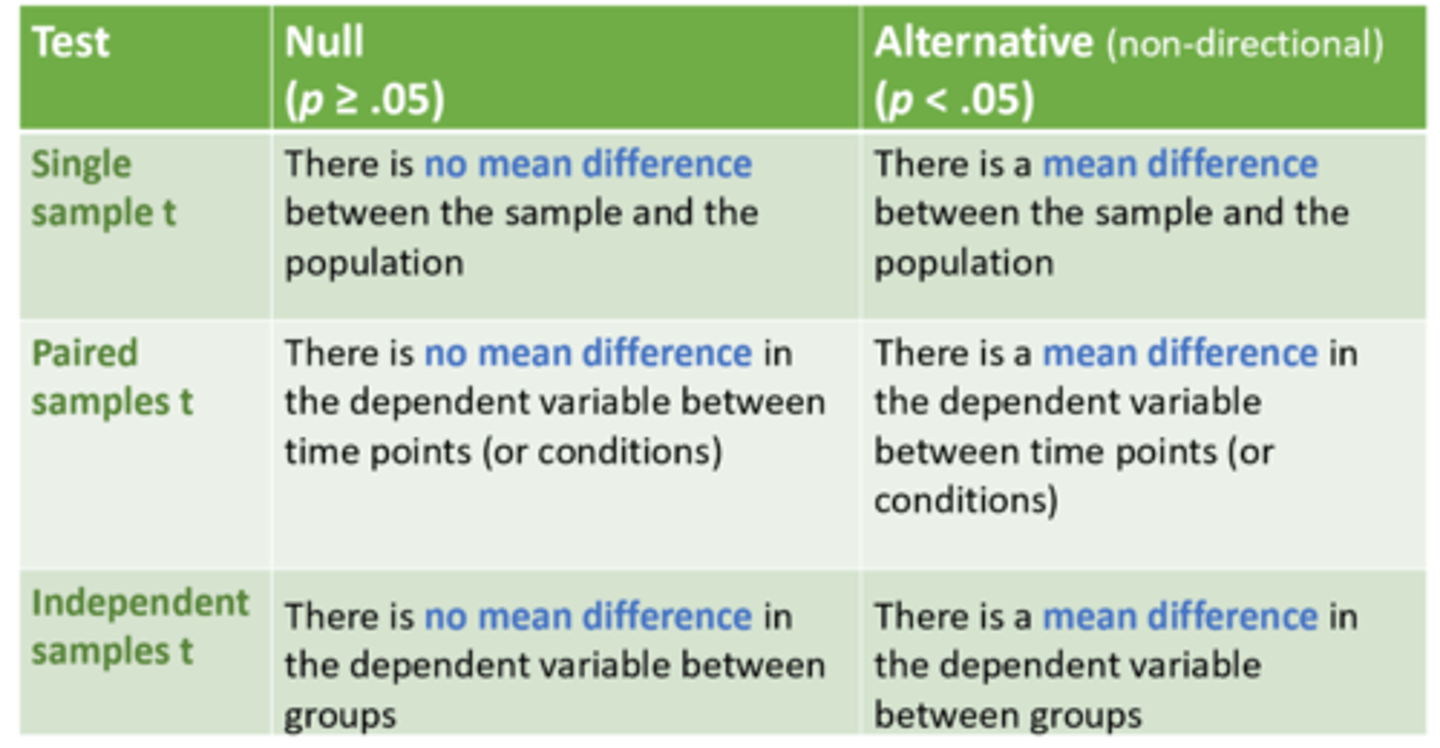
Null Hypothesis

states there is no effect on the population/ no difference between the sample mean and the population mean

alternative hypothesis

states there is an effect on the population/ a difference between the sample mean and the population mean

If data is incompatible with null hypothesis

we reject the null

if data is compatible with the null

we fail to reject the null

Two kinds of alternative hypothesis

one tailed or two tailed

One-tailed hypothesis

the direction of the affect is specified, used when there are no outcomes in a direction not studied, more powerful

two-tailed hypothesis

non-directional, used when outcomes can be in either direction, most common

Decison Rule

the rule that determines wether or not we reject or fail to reject the null

alpha (a)

the significance level or critical region used to set the descisison rule/ reject or fail to reject the null

If an observed statistic is greater than alpha/ inside the critical region

we reject the null

if an observed statistic is less than the crititcal value and falls inside the unshaded region

we fail to reject the null

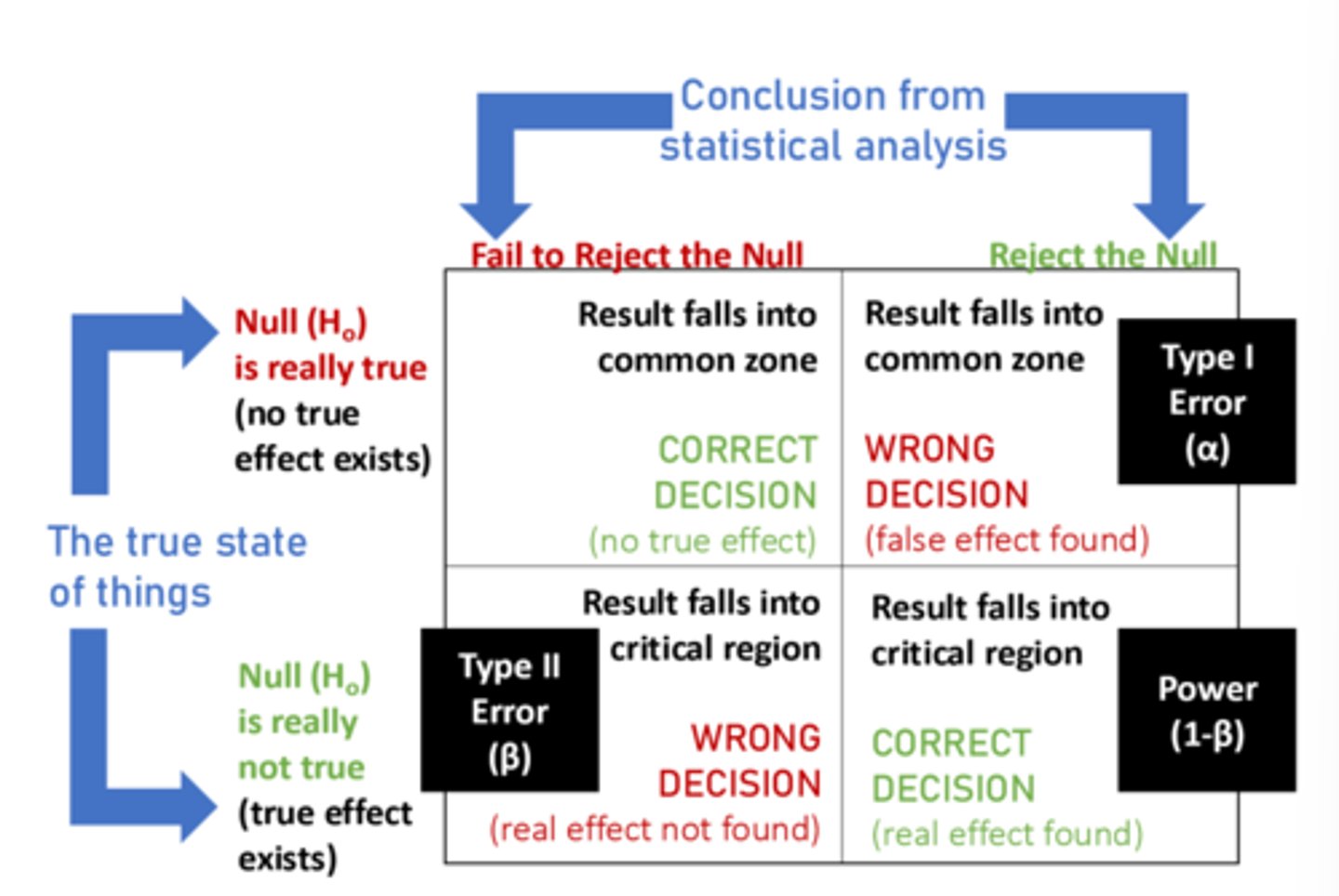
alpha represents the probability of what kind of error

type 1 error

common practice alpha value

5%, 5% possibility of being wrong

beta represents the probability of what type of error

type 2 error

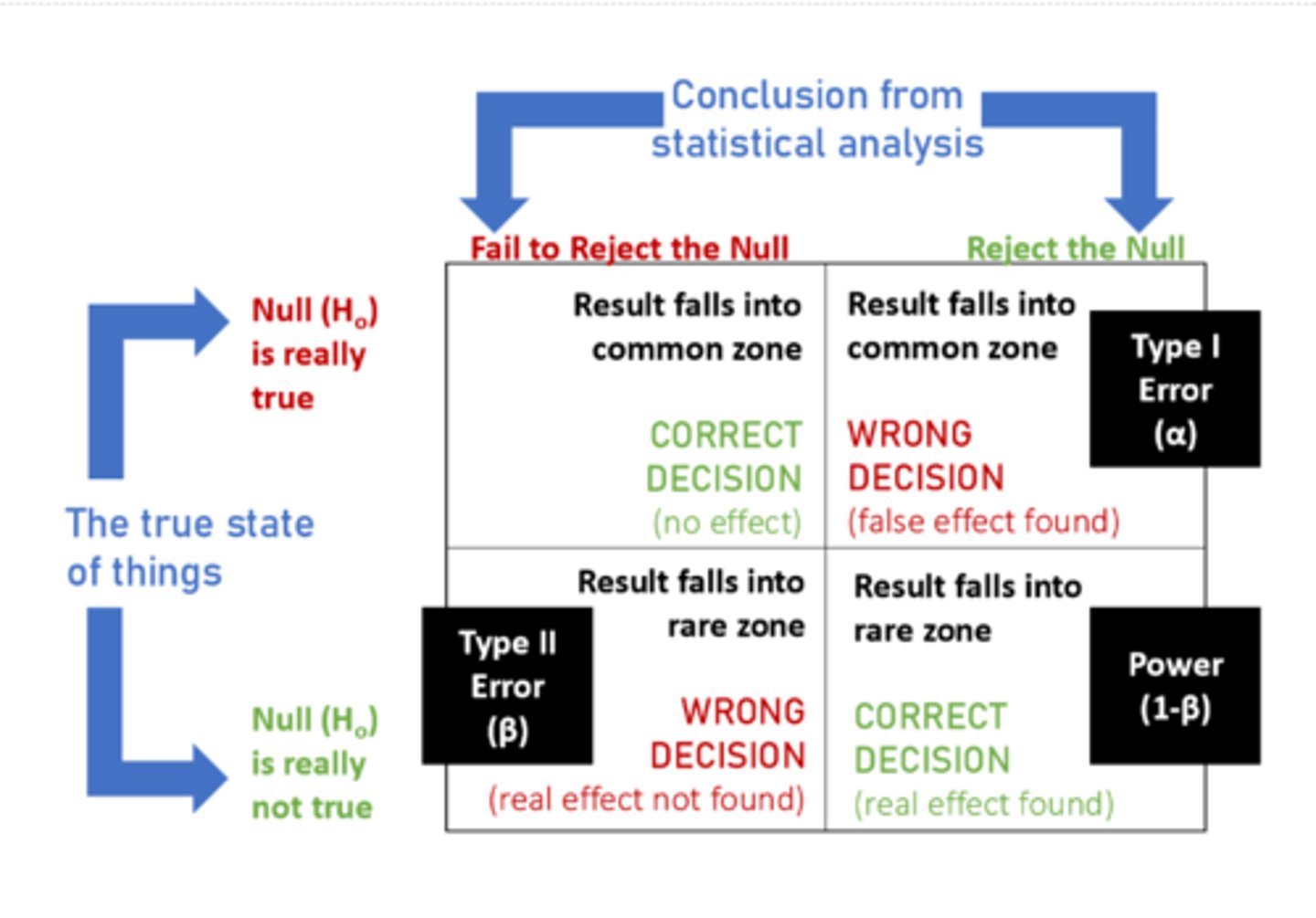
type 1 error

Rejecting null hypothesis when it is true

type 2 error

failing to reject a false null hypothesis

power

1-B, also known as a true positive

power is influenced by

sample size, effect size, alpha

4 Possible Outcomes of Hypothesis Test Table

How to identify our critical Value

critical value calculator, in appendix b of textbook

What is needed to input in critical value calculator

is the test one tailed or two tailed, what is our a value, and the n value

p value

The probability level which forms basis for deciding if results are statistically significant (not due to chance).

degrees of freedom for a single sample t test(df)

n-1

what df represents

the number of independent choice of values in a sample

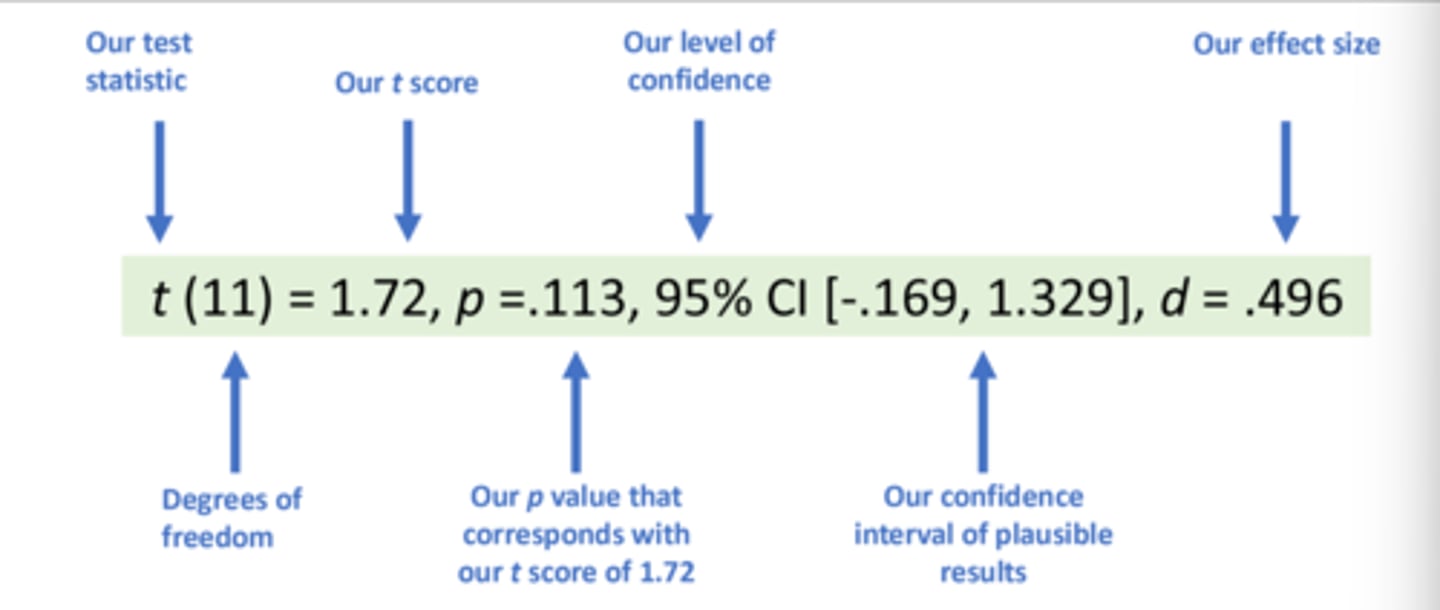
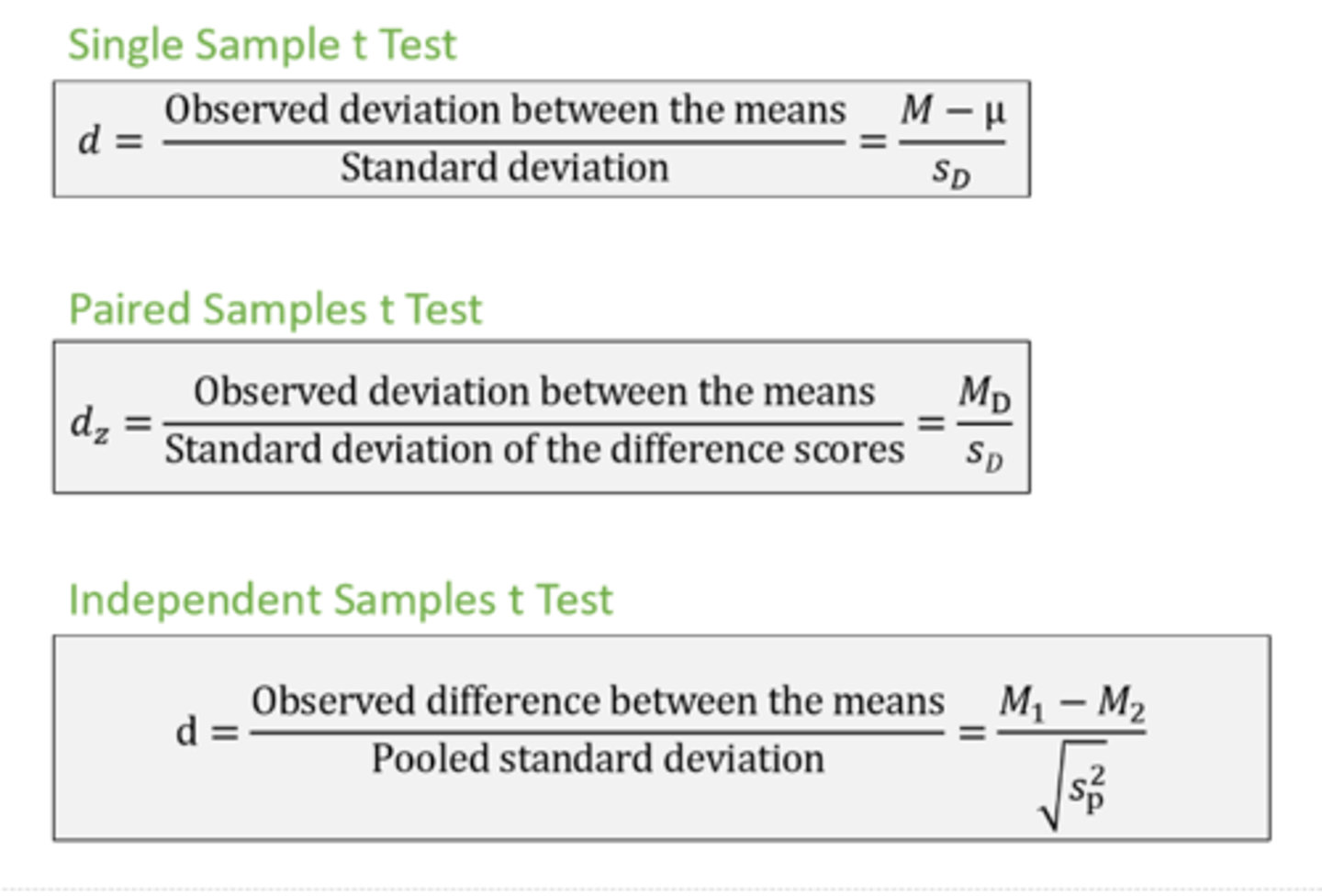
T test equation

t value = (sample mean - population mean) / standard error of sample mean

SEM (standard error of sample mean)

(SD / square root of N)

4 Steps to calculate a single sample t score

1. Calculate Sample Mean - Population Mean

2. Calculate SEM

3. Divide step 1 over step 2

4. Find p value corresponding with t score from t table online

population mean symbol

μ

p-value < alpha

we reject the null

p-value > alpha

we fail to reject the null

standardized mean difference

(sample mean- population mean)/ standard deviation

d variable represents

standardized mean difference

d=

(m-u)/s

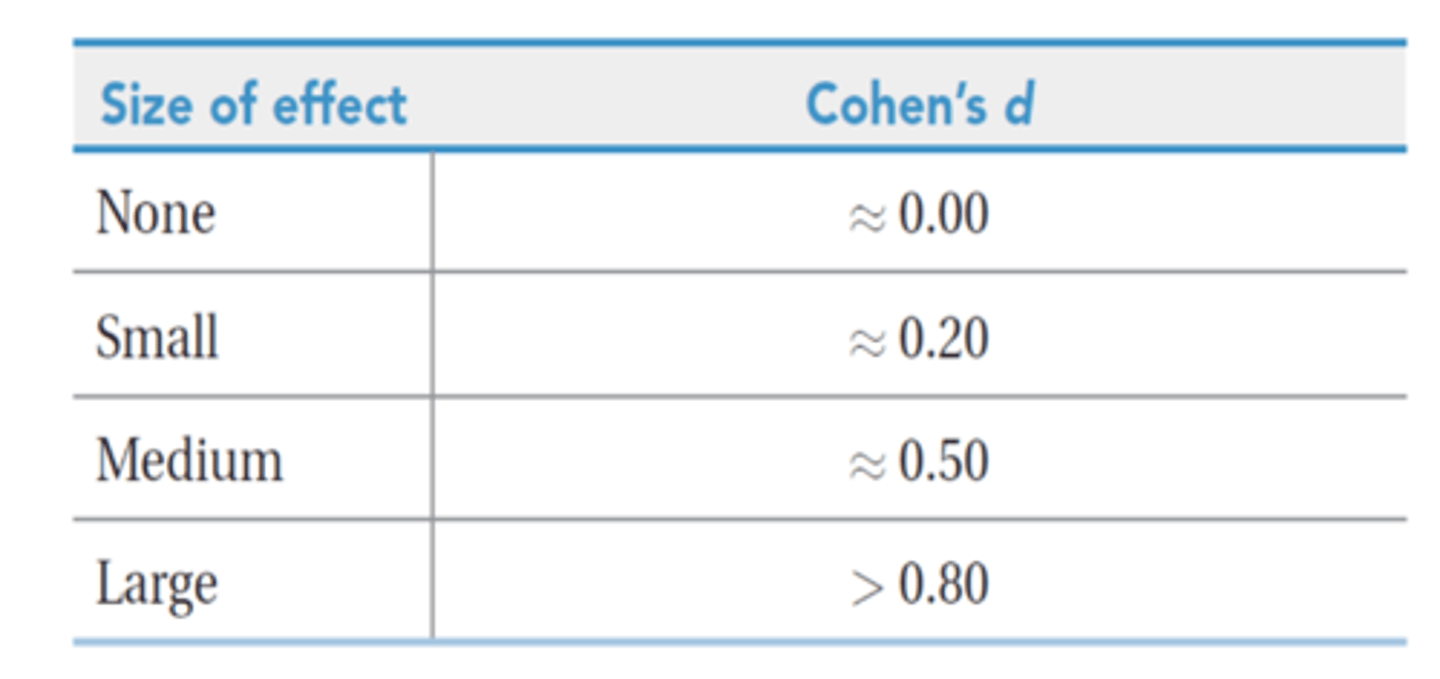
cohens d

a measure of effect size that assesses the difference between two means in terms of standard deviation, not standard error

effect size determined through

cohens d

d=0

no effect size

d=.20

small effect size

d=.50

medium effect size

d>.80

large effect size

confidence interval

estimates the likely values that might occur in a a population given sampling error

margin of error calculation

(t score from textbook appendix)(SEM of sample)

Confidence interval has

upper bound and lower bound

Calculation of CI

(sample mean-population mean) +- MOE

If the null is located within the confidence interval

we fail to reject the null, not enough evidence to suggest a mean difference

if the null is located outside the confidence interval

we reject the null, as evidence suggests a mean difference

Sample size effect on CI

Larger sample size will narrow the CI

The closer a value is to the middle of the CI

The more plausible it is

Wide CI

Are imprecise estimates

Slide for meaning of variables in a single sample t test

Related samples t test

compares two sample means which are related to eachother

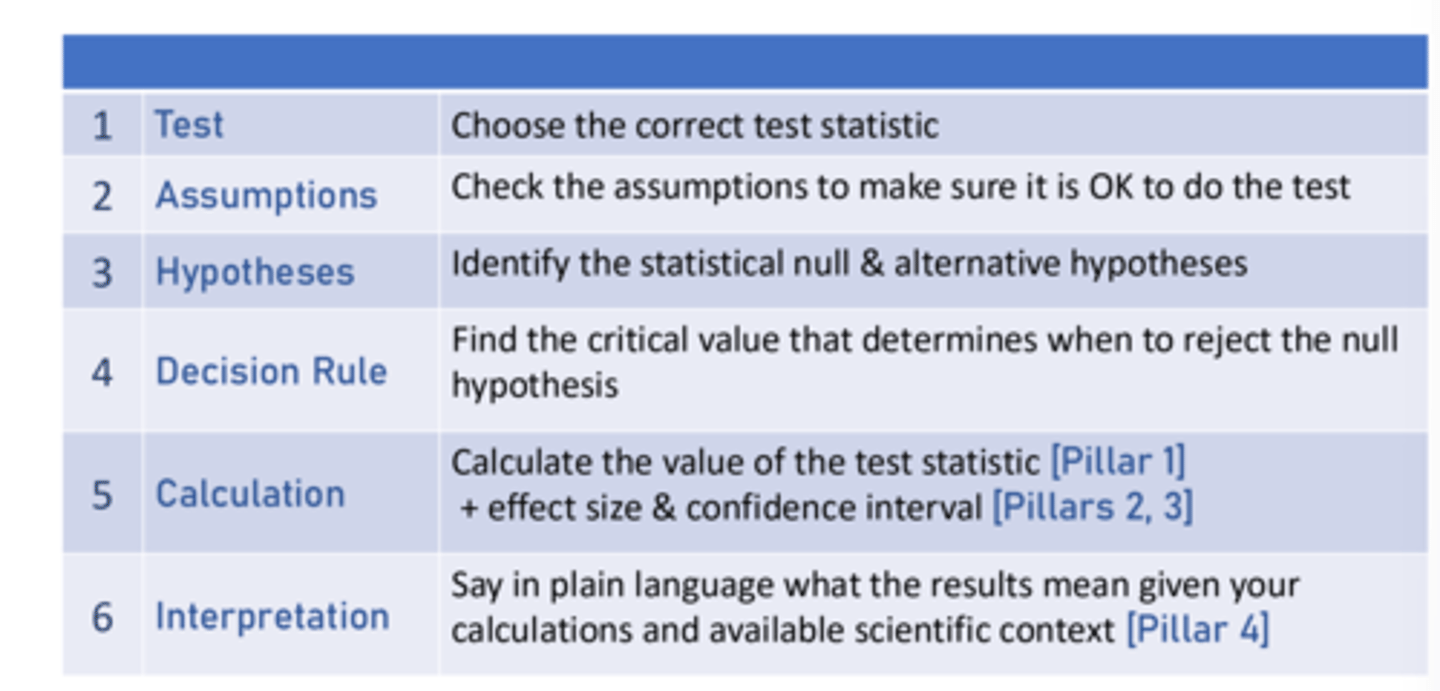
Hypothesis testing steps diagram

advantages of using a repeated measures design

requires a smaller sample and has higher probability to reject the null

Assumptions for a related samples t test

independence of data (not robust), appropriate measurement of variables (not robust), normality (robust, especially with large n)

Steps for related samples t test

1. Choose one or two sample t test

2. Check assumptions

3. Identify the null and alternative hypothesis

4. Set the descisision rule

5. Calculate t statsistic

Independent samples t test

compares two sample means that are unrelated

pooled variance

A weighted average of the two estimates of variance—one from each sample—that are calculated when conducting an independent-samples t test.

different kinds of t tests

single sample, paired samples, independent samples

paired samples t test

compares two sample means from the same group or matched groups

independent sample t test

compares two sample means from different groups

Assumptions needed for each test

Methods for assessing normality

Steps For All Statistical Analyses

Two testable assumptions

normality, homogeniety of variance

2 Methods to assess homogeneity of variance

general rule and levenes test

general rule for assessing homogeneity of variance

difference in variance should be no less than 3

Levene's test

determine if the p value is greater than or equal to .05 to be considered equal variance (robust if group sizes are equal)

Shapiro-Wilks test for normality

A statistical test used to determine if the shape of a data set approaches a normal distribution. Used when the number of subjects is equal to or greater than fifty.

How to calculate shapiro wilks test

calculates W statistic, and determines how well the data matches a normal distribution

W use

W closer to 1 means normality, W closer to 0 means not normal

Hypothesis Specific for each test

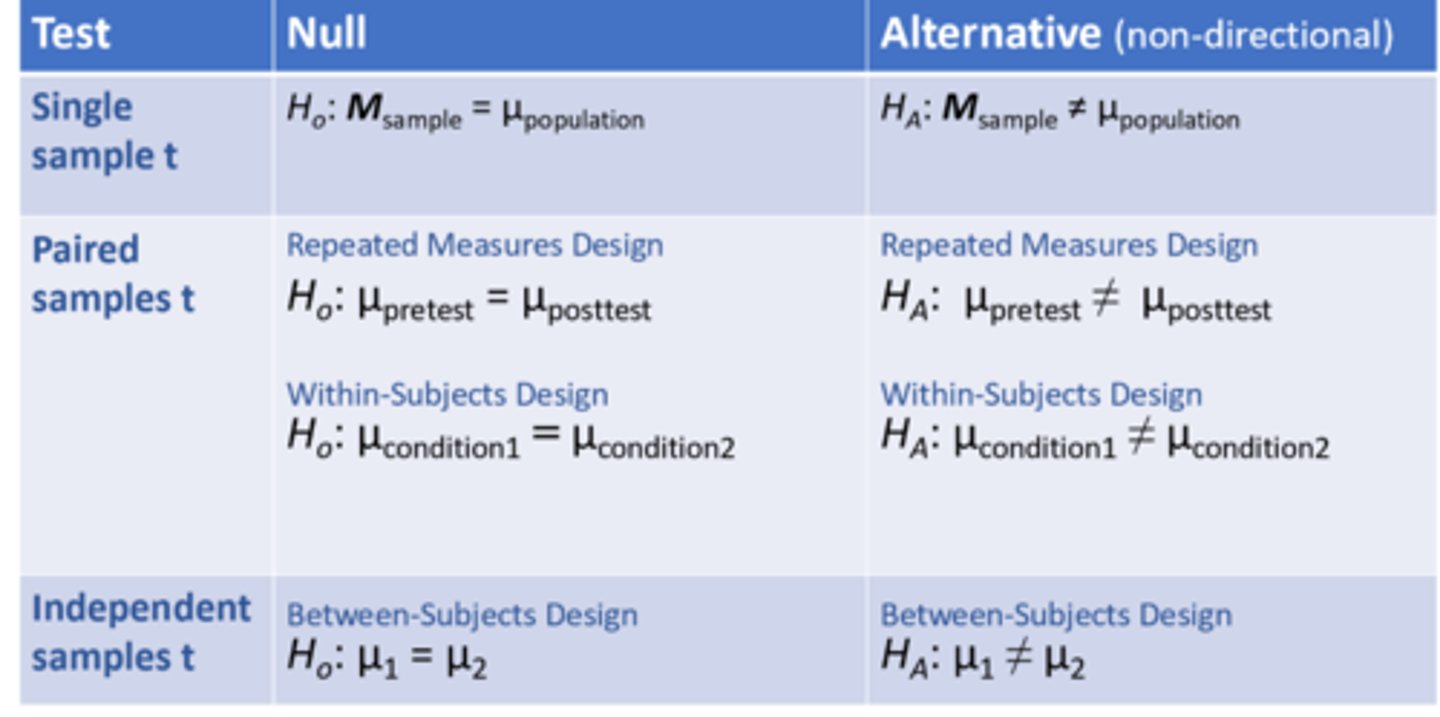
P values for each test

degrees of freedom calculation for different tests

Possible outcomes for hypothesis testing

Power is influenced by

alpha, effect size, and sample size

t calculation

mean difference/ SEM

t calculation for single sample t

t calculation for independent sample t

t calculation for paired sample t

cohens d for different tests

cohens d values

Be able to

Can you