The Relational Database Model

2Y2 | Midterms

• The relational model, introduced by E. F. Codd in 1970, is based on predicate logic and set theory.

o Predicate logic

is used extensively in mathematics to provide a framework in which an assertion (statement of fact) can be verified as either true or false.

E.F Codd

He introduced the relational model.

1970

When was the relational model first introduced?

Example: A student with a student ID of 324452 is named Mark Reyes.

o Set theory

is a part of mathematical science that deals with sets, or groups of things, and is used as the basis for data manipulation in the relational model.

Example: Set A contains 15, 23, and 52 while Set B contains 41, 52, 70, 12. It can be concluded that the A and B share a common value, 52.

• The relational model has three (3) components:

1. A logical data structure represented by relations

2. A set of integrity rules to enforce that the data is consistent and remains consistent over time

3. A set of operations that defines how data is manipulated

• A table (relation)

is as a two-dimensional structure composed of rows and columns.

• Each table row (tuple) represents data about an entity.

• Each table column represents an attribute, and each column has a distinct name.

• Each intersection of a row and column represents a single data value.

• All values in a column must conform to the same data format.

attribute domain

Each column has a specific range of values known as the ________________.

Table 1. Student Table Attribute Values

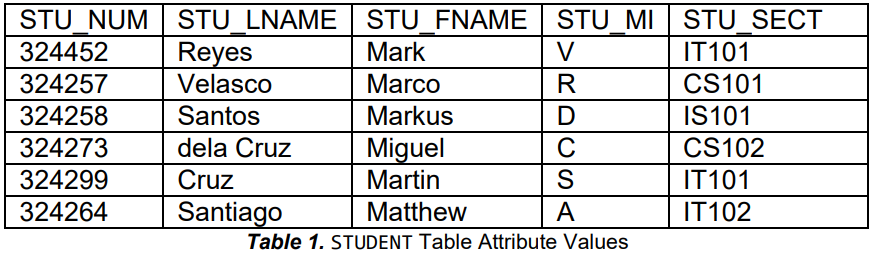
• The order of the rows and columns is not important in a DBMS.

• The following are some conclusions based on the table above.

o The STUDENT table is composed of six (6) rows/tuples and five (5) columns/attributes.

o Each of the six (6) rows describes a student. For example, row 5 describes Martin S. Cruz.

o Because the STU_MI values are limited to characters A to Z, the domain is [A, Z].

o STUNUM is the primary key since it is guaranteed unique for each student. STULNAME would not be a good primary key because students can have the same last name. Same reason applies to other attributes.

Key

is an attribute or group of attributes that determines the values of other attributes. For example, an invoice number identifies all of the invoice attributes, such as the invoice date and the customer name.

• Determination

is the state in which knowing the value of an attribute makes it possible to determine the value of another. It is based on the relationships among the attributes.

• Functional dependence

means that the value of one or more attributes determines the value of one or more other attributes.

Determinant or the key.

The attribute whose value determines another is called the

Dependent.

The attribute whose value is determined by the other attribute is called the _________.

• The standard notation for representing the relationship between attributes is: ATT_A → ATT_B

For example,

STUNUM → STULNAME

STUNUM is the determinant and STULNAME is the dependent. When given a value for STUNUM, you can determine the value for STULNAME because only one (1) value of STULNAME is associated with any given value of STUNUM.

• Functional dependence

can involve a determinant that comprises multiple attributes.

For example,

STUNUM → (STULNAME, STUFNAME, STUMI, STU_SECT)

Composite key

is a key that is composed of more than one attribute.

Key attribute

An attribute that is a part of a key is called a ____________.

• The types of keys are the following:

Superkey

An attribute or combination of attributes that uniquely identifies any row in the table.

Superkey Example

Example STUNUM and any combination with STUNUM

Ex. (STUNUM, STULNAME)

(STUNUM, STUFNAME, STU_SECT)

Candidate Key

A superkey without any unnecessary attributes

Example: STU_NUM

Primary Key

A candidate key selected to uniquely identify all other attribute values in any given row; cannot contain null entries.

Example: STU_NUM

Foreign Key

An attribute or combination of attributes in one table whose values must either match the primary key in another table or be null.

Example: STU_SECT can be a foreign key if it is used as a primary key of another table.

Secondary Key

An attribute or combination of attributes used strictly for data retrieval purposes.

Example: (STULNAME, STUFNAME, STU_MI)

Integrity Rules

Entity integrity

is the condition in which each row in a table has its own unique identity.

Referential integrity

is the conditional in which every reference to an entity instance by another entity instance is valid.

Integrity rules

are followed to maintain a good database design.

Entity Integrity

Requirement

All primary key entries are unique, and no part of a primary key may be null.

Purpose

Each row will have a unique identity, and foreign key values can properly reference primary key values.

Example

No invoice can have a duplicate number, nor can it be null; in short, all invoices are uniquely identified by their invoice number.

Referential Integrity

Requirement

A foreign key may have either a null entry, as long as it is not a part of its table’s primary key, or an entry that matches the primary key value in a table to which it is related.

Requirement

Every non-null foreign key value must reference an existing primary key value.

Purpose

It is possible for an attribute not to have a corresponding value, but it will be impossible to have an invalid entry.

Purpose

The enforcement of the referential integrity rule makes it impossible to delete a row in one table whose primary key has mandatory matching foreign key values in another table.

Example

A customer might not yet have an assigned sales representative (number), but it will be impossible to have an invalid sales representative (number).

Table example

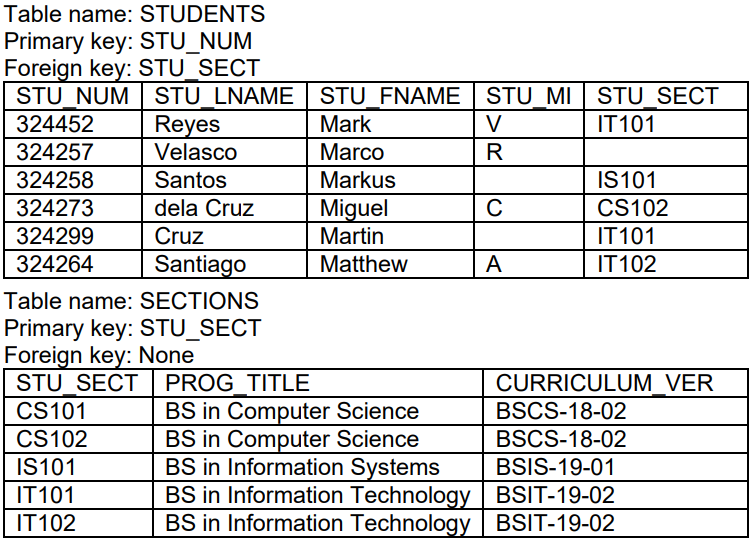
• The following are the features of the tables:

o Entity Integrity: The STUDENTS primary key (STU_NUM) column has no null entries, and all entries are unique. Similarly, the SECTIONS table’s primary key is STU_SECT, and this primary key column is also free of null entries.

o Referential Integrity: The STUDENTS table contains a foreign key, STUSECT, that links entries in the STUDENTS table to the SECTIONS table. The STUCODE row identified by the (primary key) number 324257 contains a null entry in its STUSECT foreign key because Marco Velasco does not yet have a section assigned to him. The remaining STUSECT entries in the STUDENTS table all match the STU_SECT entries in the SECTIONS table.

• To avoid nulls, special codes called flags are used to indicate the absence of some value. For example, the code NS can be used as the STUSECT entry in the second row of the STUDENTS table to indicate that Marco Velasco's section does not yet have a section assigned to him. If such a flag is used, the SECTIONS table must contain a dummy row with a STUSECT value of NS.

Relational Algebra

Data

can be manipulated to generate useful information.

Relational algebra

is a set of mathematical principles that form thebasis for manipulating relational table contents.

• Closure

The use of relational algebra operators on existing relations (tables) produces new relations is called _.

• Predicate

The condition to be evaluated is also known as .

• The eight (8) fundamental relational operators are:

SELECT

Retrieves a subset of rows

σ CONDITION (TABLE)

Example: σ STU_NUM = 324452 (STUDENTS)

UNION

Merges two union-compatible tables into a new table, dropping the duplicate rows.

Symbol: ∪

Syntax: TABLE1 ∪ TABLE2

Example: STUDENTS ∪ SECTIONS

union-compatible

Two or more tables that have the same number of columns and the corresponding columns have compatible domains are __.

INTERSECT

Retrieves rows that are common to two union-compatible tables

Symbol: ∩

Syntax: TABLE1 ∩ TABLE2

Example: STUDENTS ∩ SECTIONS

DIFFERENCE

Retrieves rows from one table that are not found in another union-compatible table

Symbol: –

Syntax: TABLE1 – TABLE2

Example ': STUDENTS – SECTIONS

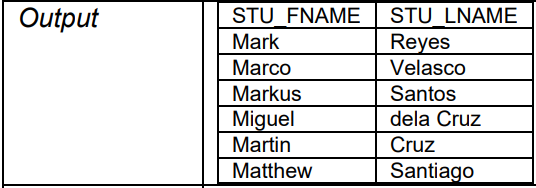
PROJECT

Retrieves a subset of columns

Syntax: π COLUMNS (TABLE)

Example: π STU_FNAME, STU_LNAME (STUDENTS

Symbol: π

JOIN

Retrieves rows from two tables based on criteria (Ex. Rows with common values in their common attributes)

Symbol: ⨝

Syntax: TABLE1 ⨝ TABLE2

Example: STUDENTS ⨝ SECTIONS

PRODUCT

Retrieves possible pairs of rows from two tables (Cartesian Product)

Symbol: x

Syntax: TABLE1 x TABLE2

Example: STUDENTS x SECTIONS

DIVIDE

Retrieves values

÷

Syntax: TABLE1 ÷ TABLE2

Example: STUDENTS ÷ SECTIONS