Stat. Week 2 - BIVARIATE PEARSON CORRELATION

Pearson Correlation

Main idea:

• If two variables are dependent of each other, Pearson’s r gives us information about the strength of this association

• We don’t know if one variable causes the other (no causal direction)

• Changes in one variable are associated with changes in the other variable

Calculation Pearson’s r

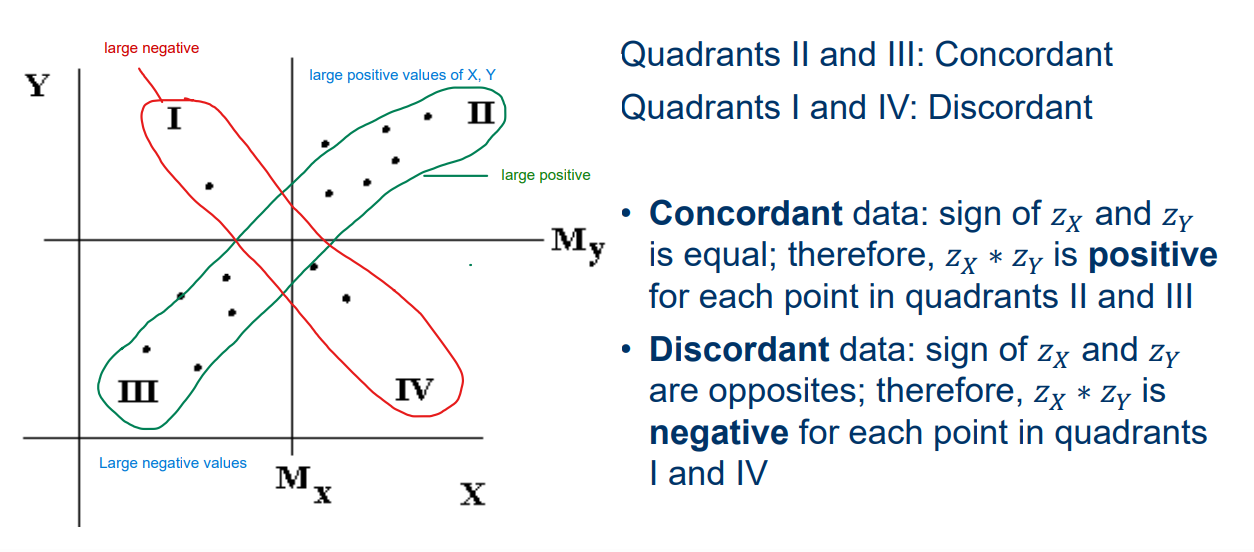
It is helpful to divide a X, Y scatterplot in 4 quadrants

Concordant data points: data points that lie above the mean of both X and Y or below the mean of both X and Y > II and III

Discordant data points: data points that lie below the mean of X and above the mean of Y, or above the mean of X and below the mean of Y > I and IV

Assumptions

Scores of the X and Y variables:

1. are quantitative (or both dichotomous)

2. are linearly related

3. have a bivariate normal distribution

4. do not have extreme outliers

5. Homoscedasticity: Y-scores have the same variance across levels of X (and vice versa)

T-test

Factors that can influence Pearson’s

1. Data patterns in X, Y plot (see ‘The cross’)

2. Selection of Extreme Groups

3. Correlations of samples with combined groups

4. Extent to which r is controlled by other variables

5. Bivariate outliers

6. Different shapes of distribution of X and Y (Normality assumption)

7. Curvilinear or nonlinear relationships

8. Transformation of data (e.g. log)

9. Attenuation as a result of unreliability of measurement*; unreliable measurements weaken the correlation between such measurements

10. Artificial part-whole correlations (e.g. using a sumscore)

11. Aggregated data (Simpson’s paradox and the ecological fallacy)

Pearson’s and causal conclusions

the following are conditions for interpreting an association between X and Y as causal:

1. Cause X and outcome Y must correlate

2. Cause X must precede outcome Y in time

3. Association between X and Y must not be spurious (no common cause)

4. A theory is available that explains the association between X and Y

Adding a third variable

Elaboration of an Association

1.      Think about how the variables Y, X1 and control variable X2 are theoretically associated with each other (make conceptual model)

2.      Estimate the uncontrolled association between X1 and Y. This yields a measure of association, e.g. 𝑟_1𝑌

3.      Keep the association between X1 and Y constant for the influence of X2 (control for X2)

4.      Inspect whether the (controlled) association between 𝑟_1𝑌 has changed

5.      Depending on the nature of the change in association and keeping in mind your theoretical model (step) we decide that there is a particular type of association between the variables

Partial correlation coefficient

It measures the linear association between X1 and Y while controlling for X2.

Partial: That specific part of the total correlation associated with X1, and not associated with X2.

Bivariate Pearson Correlation

The numerator r_Y1−(r₁₂×r_2Y) adjusts the raw correlation r_Y1 by removing the effect that X2 has on both X1and Y.

This adjustment helps isolate the unique relationship between X1 and Y, independent of X2​.

 How It Works:

r₁₂×r_2Y is subtracted from r_Y1 because it represents the indirect association between X1 and Y through X2. This part accounts for any confounding effect of X2 on the observed correlation between X1​ and Y.

Interpretation:·      

If the partial correlation pr₁​ is significant, it indicates that X1and Y are correlated even after controlling for X2.

·       A larger effect of X2 (reflected in r₁₂ and r_2Y would decrease the value of the numerator, reducing the partial correlation pr₁.

Results