Discrete Mathematics

Discrete Objects

The foundation for formal methods, such as mathematical approaches to software / hardware, software engineering, and software testing.

Set Definition

A collection of unique and unordered elements.

Set Example

A = {1, 2}

Set Conventions

• Sets are named with a capital letter

• Elements are named with a lowercase letter.

Set Membership

a ∈ A

Set Non-Membership

b ∉ A

Defining Infinite Sets

Sets can be enumerated by defining a property that all of its elements must satisfy.

Defining Infinite Sets Example

A = { x | x is an integer and x > 0}

Union of Sets Definition

Forms a new set from two sets consisting of all elements that are in either of the original sets.

Union of Sets Example

A = {1, 2, 3, 4, 5}

B = {3, 4, 5, 6, 7}

A ∪ B = {1, 2, 3, 4, 5, 6, 7}

Intersection of Sets Definition

Forms a new set from two sets, consisting of all the elements that are in both of the original sets.

Intersection of Sets Example

A = {1, 2, 3, 4, 5}

B = {3, 4, 5, 6, 7}

A ∩ B = {3, 4, 5}

Difference of Sets Definition

Forms a new set from two sets, consisting of all elements from the first set that are not present in the second set.

Difference of Sets Example

A = {1, 2, 3, 4, 5}

B = {3, 4, 5, 6, 7}

A — B = {1, 2}

B — A = {6, 7}

Cartesian Product of Sets Definition

Forms a new set from two sets, consisting of all the ordered pairs <1, 2>, where 1 is an element from the first set, and 2 is an element from the second set.

Cartesian Product of Sets Example

A = {a1, a2, a3}

B = {b3, b4, b5}

A × B = {<a1, b3>, <a1, b4>, <a1, b5>,

<a2, b3>, <a2, b4>, <a2, b5>,

<a3, b3>, <a3, b4>, <a3, b5>}

Ordered Pair Definition

A pair of objects with an order associated with them.

Ordered Pair Equality

Ordered Pairs <a, b> and <b, a> are not equal.

Set Operations Precedence

Union, intersection, difference, and Cartesian product are all equal in the order of precedence.

Set Cardinality

The number of elements within a set.

Set Cardinality Example

A = {1, 2, 3, 4, 5}

|A| = 5

Empty Set Definition

A set which contains no elements.

Empty Set Example

A = Ø

Disjoint Set Definition

Two sets are disjoint if they have no elements in common — their intersection returns an empty set.

Disjoint Set Example

A = {1, 2, 3}

B = {4, 5, 6}

A ∩ B = Ø

Equal Set Definition

Two sets are equal if they have the same elements — every single element in A is also an element in B, and vice versa.

Equal Sets Example

A = {1, 2, 3, 4, 5}

B = {1, 2, 3, 4, 5}

Non-Equal Sets Definition

Two sets are not equal if they do not have the same elements — at least one element in A is not in B or vice versa.

Non-Equal Set Example

A = {1, 2, 3, 4, 5}

B = {1, 2, 3, 4}

Set of Sets Definition

A set can contain another set as an element.

Set of Sets Example

A = {1, {2, 3}}

Subsets Definition

A is a subset of B if every element of A is also an element of B.

Subsets Example

A = {1, 2, 3, 4}

B = {1, 2, 3, 4, 5}

A ⊆ B

Proper Subsets Definition

A is a proper subset of B if :

• A is a subset of B

• A is not equal to B

Proper Subset Example

A = {1, 2, 3, 4}

B = {1, 2, 3, 4, 5}

A ⊂ B

Non-Subsets Definition

A is not a subset of B if at least one element of A is not in B.

Non-Subsets Example

A = {1, 2, 3, 4, 5}

B = {1, 2, 3, 4}

A ⊄ B

Supersets Definition

A is a superset of B if every element of B is an element of set A.

Supersets Example

A = {1, 2, 3, 4, 5}

B = {1, 2, 3, 4}

A ⊇ B

Proper Supersets Definition

A is a proper superset of B if:

• Every element in B is an element of A

• A is not equal to B

Proper Subsets Example

A = {1, 2, 3, 4, 5}

B = {1, 2, 3, 4}

A ⊃ B

Non-Supersets Definition

A is not a superset of B if at least one element of B is not in A.

Non-Supersets Example

A = {1, 2, 3, 4}

B = {1, 2, 3, 4, 5}

A ⊅ B

Universal Sets Definition

A non-empty set of all the possible elements relevant to the solution of a specific problem, denoted by U.

Complement Sets Definiton

The difference between the universal set and a given set.

Binary Relation Definition

Element a is related to element b through the relation R, where A × B is a superset of R.

Binary Relation Example

A = {a1, a2, a3, a4, a5}

B = {b1, b2, b3, b4, b5}

R = {<a1, b2>, <a2, b3>, <a3, b1>, <a4, b5>, <a5, b4>}

Ordered n-Tuples Definition

A set of n objects with an order associated with them.

Ordered n-Tuples Example

<a1, a2, a3, …, an>

n-ary Relation Definition

Involves n sets and can be described by a set of n-tuples.

Table Representation of Relation

A = {a, b, c}

B = {1, 2, 3}

C = {x, y, z}

R ⊆ A × B × C

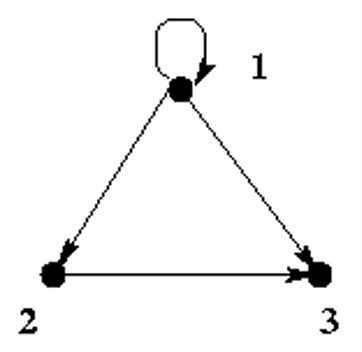
Diagraph Representation of Relation

A = {1, 2, 3}

B = {<1,1>, <1,2>, <1, 3>, <2, 3>}

R = <A, B>

Union of Relations Definition

Forms a new relation from two relations consisting of all elements that are in either of the original relations.

Union of Relations Example

A = {1, 2}

B = {x, y}

R1 = {<1, x>, <2, y>}

R2 = {<1, x>, <2, x>}

R1 ⋃ R2 = {<1, x>, <2, y>, <2, x>}

Intersection of Relations Definition

Forms a new relation from two relations consisting of all elements that are in both of the original relations.

Intersection of Relations Example

A = {1, 2}

B = {x, y}

R1 = {<1, x>, <2, y>}

R2 = {<1, x>, <2, x>}

R1 ⋂ R2 = {<1, x>}

Difference of Relations Definition

Forms a new relation from two relations, consisting of all elements from the first relation that are not present in the second relation.

Difference of Relations Example

A = {1, 2}

B = {x, y}

R1 = {<1, x>, <2, y>}

R2 = {<1, x>, <2, x>}

R1 — R2 = {<2, y>}

R2 — R1 = {<2, x>}

Cartesian Product of Relations Definition

Forms a new relation from two relations, consisting of all the ordered pairs <1, 2>, where 1 is an element from the first relation, and 2 is an element from the second relation.

Cartesian Product of Relations Example

A = {1, 2}

B = {x, y}

R1 = {<1, x>, <2, y>}

R2 = {<1, x>, <2, x>}

R1 × R2 = {<1, x, 1, x>, <1, x, 2, x>, <2, y, 1, x>, <2, y, 2, x>}

Subrelations Definition

R1 is a subrelation of R2 if every ordered tuple that is an element of R1 is also an element of R2.

Subrelations Example

A = {1, 2}

B = {x, y}

R1 = {<1, x>, <2, y>}

R2 = {<1, x>, <1, y>, <2, y>}

R1 ⊆ R2

Symmetry of Relations Definition

When a relation contains both <a, b> and <b, a>, for any a and b in A.

Symmetry of Relations Example

A = {1, 2, 3, 4, 5}

R = {<1, 2>, <2, 1>, <3, 5>, <5, 3>}

Transitivity of Relations Definition

If a relation contains <a, b> and <b, c>, it contains <a, c> also.

Transitivity of Relations Example

A = {1, 2, 3, 4, 5}

R = {<1, 3>, <3, 5>, <1, 5>}

Reflexivity of Relations Definition

When a relations contains <a, a> for every element in A.

Reflexivity of Relations Example

A = {1, 2, 3, 4, 5}

R = {<1, 1>, <2, 2>, <3, 3>, <4, 4>, <5, 5>}

Irreflexivity of Relations Definition

When a relation does not contain <a, a> for every element in A.

Irreflexivity of Relations Example

A = {1, 2, 3, 4, 5}

R = {<1, 1>, <2, 2>, <3, 3>, <4, 4>}

Equivalence of Relations Definition

When a relation is reflexive, symmetric, and transitive.

Equivalence of Relations Example

A = {1, 2, 3, 4, 5}

B = {1, 2, 3, 4, 5}

R = {<1, 1>, <2, 2>, <3, 3>, <4, 4>, <5, 5>}

Function Definition

A special type of binary relation which associates each unique element of a set with an element of another set.

Domain of Functions Definition

The set of all input elements of the function.

Domain of Functions Example

A = {1, 2, 3, 4, 5} ← Domain

B = {a, b, c, d, e}

F : A → B

F = {<1, a>, <2, b>, <3, b>, <4, d>, <5, c>}

Codomain of Functions Definition

The set of all possible outputs of the function.

Codomain of Functions Example

A = {1, 2, 3, 4, 5} 

B = {a, b, c, d, e} ← Codomain

F : A → B

F = {<1, a>, <2, b>, <3, b>, <4, d>, <5, c>}

Range of Functions Definition

The set of all actual outputs of the function.

Range of Functions Example

A = {1, 2, 3, 4, 5}

B = {a, b, c, d, e}

F : A → B

F = {<1, a>, <2, b>, <3, b>, <4, d>, <5, c>}

G = {a, b, c, d} ← Range

Image of Functions Definition

The single output value produced by input x when passed through f.

Preimage of Functions Definition

The single input value which, when passed through f, produces output y.

Inverse Functions Definition

Reverses the domain and codomain and produces a function with the same ordered pairs as the original, simply reversed.

Inverse Functions Example

f = A → B

f^-1 = B → A

Surjective Functions Definition