Week 1 Lecture 2 - DFAs and NDFAs

How is a deterministic finite state automata specified?

M = ⟨Q, Σ, δ, i, F⟩ where:

→ Q, a finite set of states
→ Σ, a finite set of possible input symbols, the alphabet → δ, a transition function Q × Σ → Q
→ i, an initial state (i ∈ Q)
→ F , a set of final states (F ⊆ Q)

Defining acceptance in a DFA

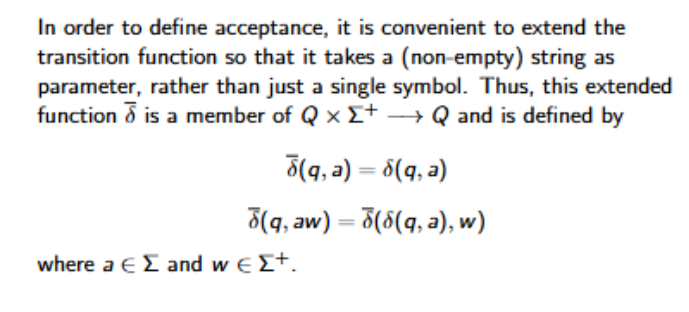
When is a non empty string S accepted by a DFA?

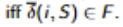
When is the empty string λ accepted by a DFA?

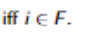
When is a language L accepted by an FSA (DFA)

iff M accepts every string S in L and nothing else

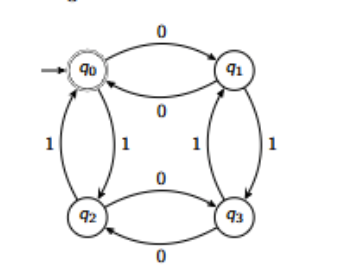
Construct the DFA for the following language:

L = {w | w has an even number of 0s and an even number of 1s

The (minimum) job of the states of this DFA is to assess the parity of 0s and 1s.
Hence a four state machine:
• q0 — even 0s and even 1s.
• q1 — odd 0s and even 1s.
• q2 — even 0s and odd 1s.
• q3 — odd 0s and odd 1s.

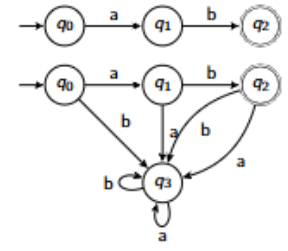
What is the difference between the languages accepted by the following DFAs?

q₃ is known as a junk state (or sink, or dead). It is often omitted.

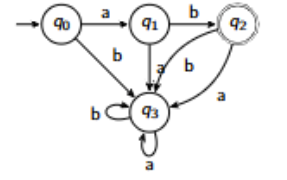
Stack the transition labels on the pairs of stacks in this DFA

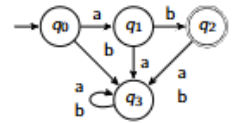
What restriction does an NDFA (non-deterministic finite-state automa relax?

In a DFA, for every state there is one next state. In an NDFA, there can be multiple.

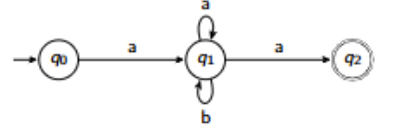
How is this an example of an NDFA?

At q₁ , there is a self loop for (a) but it also passes on to q₂ (the accepting state). Because there are 2 transitions for a, it is an NDFA.

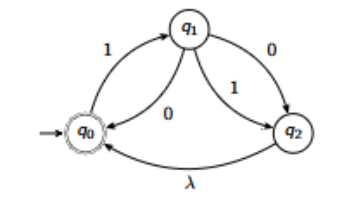
How is this an example of an NDFA, and would it accept ‘11’?

The input on q₀ of the empty string means that if you have a string like ‘11’, even though it will end up at q₂ , because the transition requires no input, it is still accepted.

Because of the λ transition, it is an NDFA.

Advantages of non-determinism:

→ Problems involving search can be expressed more neatly using NDFA.

→ Applying algorithms to create or modify FSA, the results are sometimes non-deterministic.