StemUp: OCR A A level Physics 6.1 Capacitors

What is a capacitor? (2)

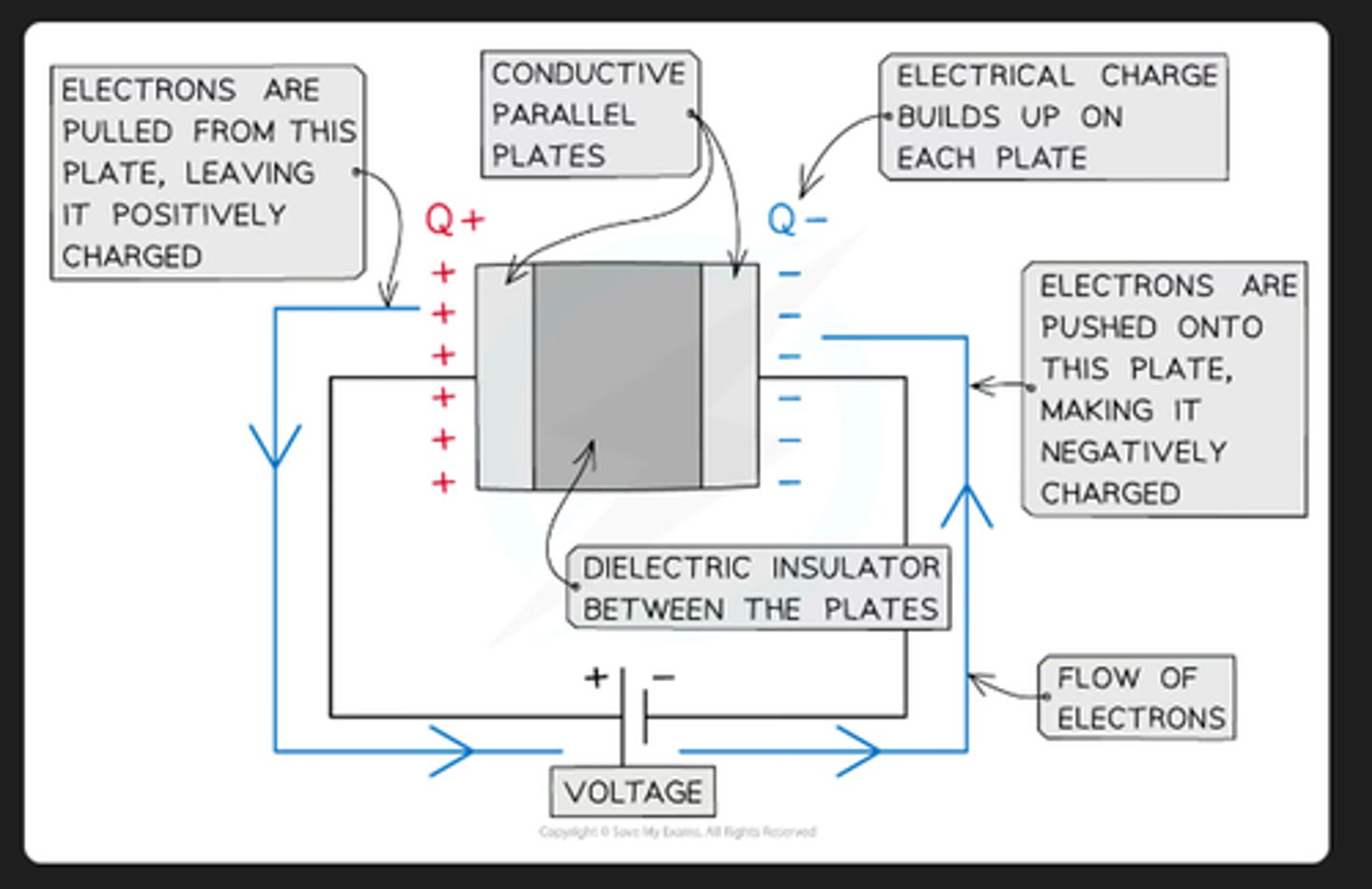
- A capacitor is an electrical component that stores charge on two separated metal plates.

- An insulator is placed between the plates to stop charge travelling across the gap between the plates.

How is charge prevented from travelling across the gap in a capacitor? (1)

An insulator (sometimes called a dielectric) is placed between the plates to stop charge travelling across the gap between the plates. The electrons cannot flow through the insulator.

What is meant by the capacitance? (1)

This is defined as the charge stored per unit potential difference between the two plates in a capacitor.

What is the equation for capacitance? (2)

- This is given by C = Q / V

- Where C is the capacitance measured in Farads (F), Q is the stored charge (C) and V is the potential difference (V).

What is the unit for capacitance? (1)

This is given by the Farad (F).

How is a capacitor charged? (3)

- When connected to a circuit, electrons are pulled away from the plate connected to the positive end of the cell/batter (this plate is positively charged.)

- The electrons move around the circuit and build up on the other plate (negatively charged plate)

The charging stops when no more electrons can be pushed on the negatively charged plate due to electrostatic repulsion from the electrons on it.

How is a capacitor discharged? (2)

- Capacitors are discharged through a resistor which has no power supply.

- The electrons can now move through the resistor to the opposite plate until there are equal electrons on both plates and no potential difference between them.

How is the total capacitance found for two or more capacitors in series? (1)

This is given by the equation: 1 / C = 1 / C_1 + 1 / C_2 + ......

How is the total capacitance found for two or more capacitors in parallel? (1)

This is given by: C = C_1 + C_2 + .....

What does a potential difference-charge graph look like for a capacitor? (1)

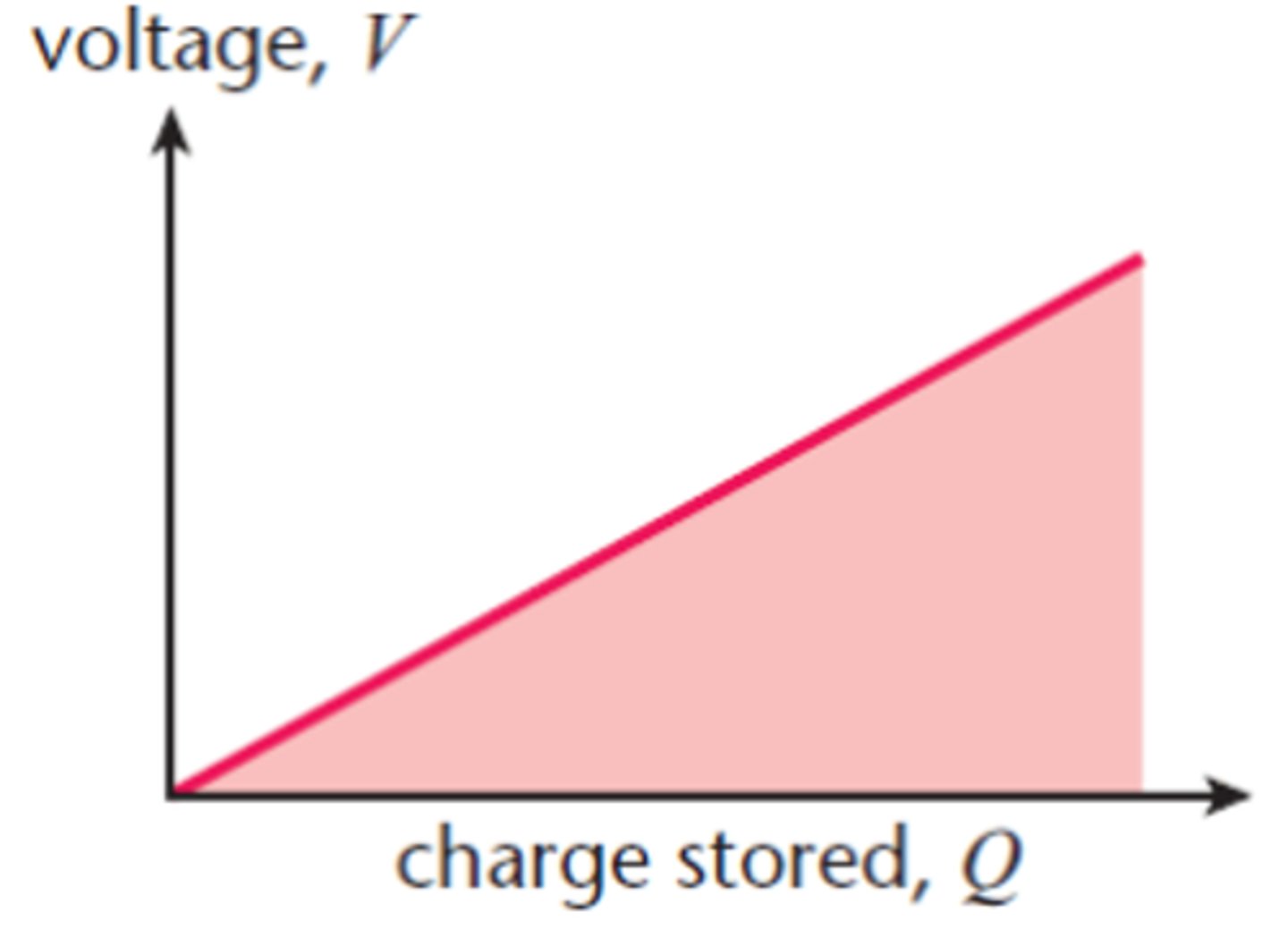
How is the energy stored in a capacitor found from a potential difference-charge graph? (1)

The area under the graph is equal to the energy stored in a capacitor.

What is the equation for energy stored in a capacitor in terms of charge and potential difference? (2)

- This is the area under the graph given by: W = 1 / 2 QV​

Where W is the energy stored in the capacitor (J), Q is the charge stored in the capacitor (C) and V is the potential difference across the capacitor (V).

What is the equation for energy stored in a capacitor in terms of capacitance and potential difference? (2)

- From W = 1 / 2 QV we know Q = CV so we can rewrite this to be W = 1 / 2 V^2C

- Where W is the energy stored in the capacitor (J), C is the capacitance of the capacitor (F) and V is the potential difference across the capacitor (V).

What is the equation for energy stored in a capacitor in terms of capacitance and charge? (2)

- From W = 1 / 2 QV we know V = C/Q so we can rewrite this to be: 1 / 2 Q^2 / C

- Where W is the energy

stored in the capacitor (J), C is the capacitance of the capacitor (F) and Q is the charge stored in the capacitor (C).

How are capacitors useful in energy storage? (2)

- They are used to store and discharge large amount of energy in a small amount of time.

- This can be useful for short pulses of energy such as camera flashes.

How does a capacitor discharge through a resistor? (3)

- A capacitor is connected to a resistor with a switch as shown in digram:

- The switch is disconnected from the power supply so only the capacitor and resistor are connected together.

- The electrons can now move through the resistor to the opposite plate until there are equal electrons on both plates and no potential difference between them.

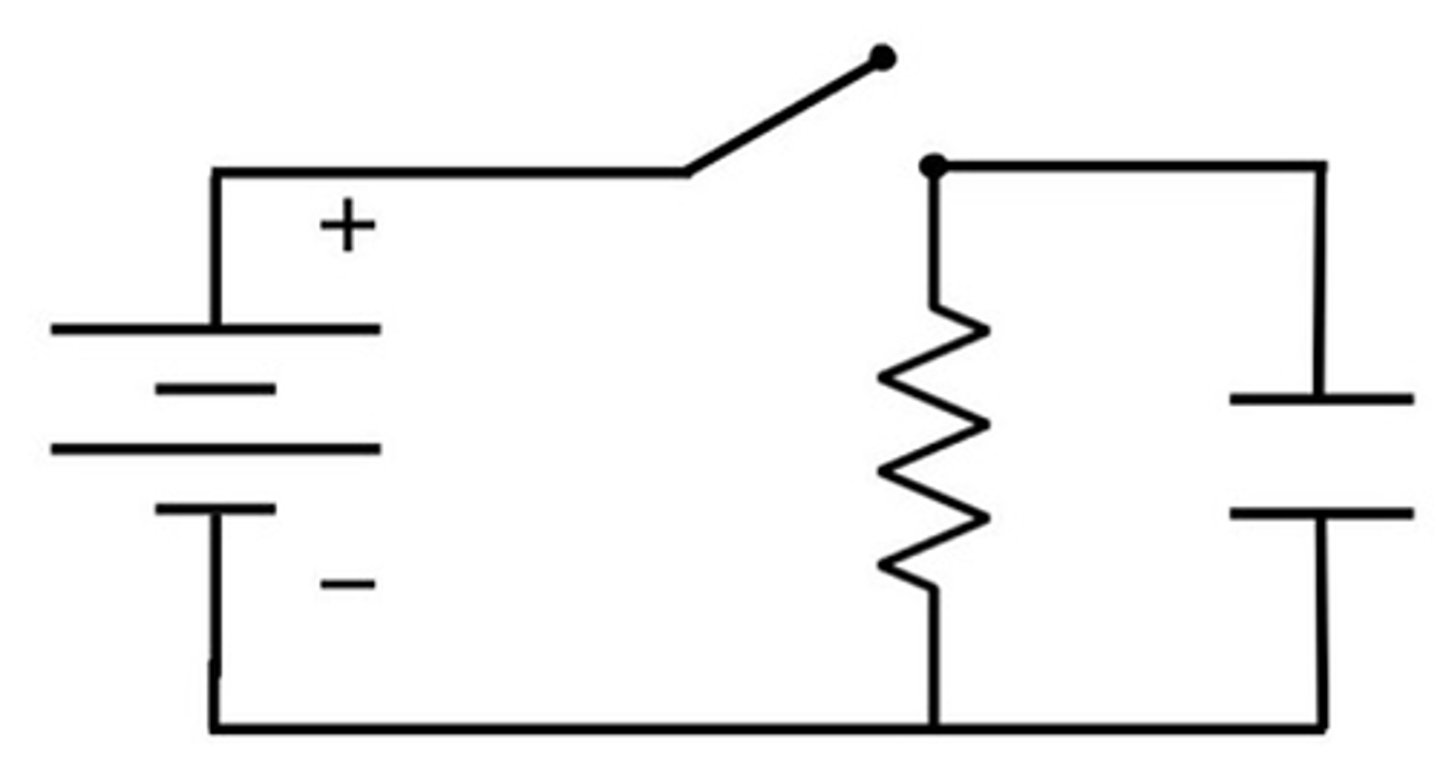
What is meant by the time constant for capacitors? (2)

- This is the amount of time taken for the charge, current or voltage to decrease to 37% of its original value when discharging (1 / e% ≈ 37%).

- Or it can be defined as the time taken for the charge, current or voltage to rise to 63% of its maximum value.

What is the equation for the time constant? (2)

- This is given by Τ = RC

- Where Τ is the time constant (s), R is the resistance of the resistor the capacitor is discharging through (Ω) and C is the capacitance of the capacitor (F).

What is the equation for current in a discharging capacitor? (2)

- This is given by: I = I_0 e^-t / RC

- Where I is the current (A) I_0 is the initial current before discharging (A), t is the time taken whilst discharging (s), R is the resistance of the resistor the capacitor is discharging through (Ω) and C is the capacitance of the capacitor (F).

What is the equation for charge in a discharging capacitor? (2)

- This is given by: Q = Q_0 e^-t /RC (exponential decay)

- Where Q is the charge (C) Q_0 is the initial charge before discharging (C), t is the time taken whilst discharging (s), R is the resistance of the resistor the capacitor is discharging through (Ω) and C is the capacitance of the capacitor (F).

What is the equation for potential difference in a discharging capacitor? (2)

- This is given by: V = V_0 e^-t /RC

- Where V is the potential difference (V) V_0 is the initial potential difference before discharging (V), t is the time taken whilst discharging (s), R is the resistance of the resistor the capacitor is discharging through (Ω) and C is the capacitance of the capacitor (F).

What is the equation for current in a charging capacitor? (2)

- This is given by: I = I_0 e^-t /RC

- It is the same as its discharging equation as it is still exponentially decaying as the charge flow gets smaller over time as electrons reach the plate.

What is the equation for charge in a charging capacitor? (1)

This is given by Q = Q_0 (1-e^-t /RC​)

What is the equation for potential difference in a charging capacitor? (1)

This is given by V = V_0 (1-e^-t /RC)​

How can log graphs be used to find the value of the time constant of a capacitor? (2)

- We can take natural logarithms of both sides (in this example current) which becomes ln I = ln I_0 e^-t /RC

- The natural logarithm and e (exponential) cancel out and this leaves the equation: ln I = ln I_0 - t /RC so the y-intercept is equal to -t /RC and the value of RC (time constant) can be found

What is the equation relating the change in charge over the change in time for a discharging capacitor? (2)

- This is given by: ∆Q \ ∆t = -Q /RC

- Where ∆Q is the change in charge (C), ∆t is the change in time (s), Q is the charge stored in the capacitor (C), R is the resistance of the resistor the capacitor is discharging through (Ω) and C is the capacitance of the capacitor (F).

How can the equation relating the change in charge over the change in time for a discharging capacitor be modelled using a graph? (2)

- The equation ∆Q \ ∆t = -Q /RC can be modelled by calculating the change in charge over a small change in time multiple times in a large time period and this could be graphed to find the approximate change in charge over the time period.

- This would look like an exponential decay graph as the charge will decrease as the capacitor discharges.

How can the equation relating the change in charge over the change in time for a discharging capacitor be modelled using a spreadsheet? (2)

- The equation ∆Q \ ∆t = -Q /RC can be modelled by calculating the change in charge over a small change in time multiple times in a large time period and this could be tabulated into a spreadsheet.

- The time taken for the charge to decrease by any given percentage should be the same throughout the spreadsheet.

What is an exponential decay graph? (1)

This is a graph that looks like:

There is rapid decrease at the beginning but the rate of decrease slows down over time.

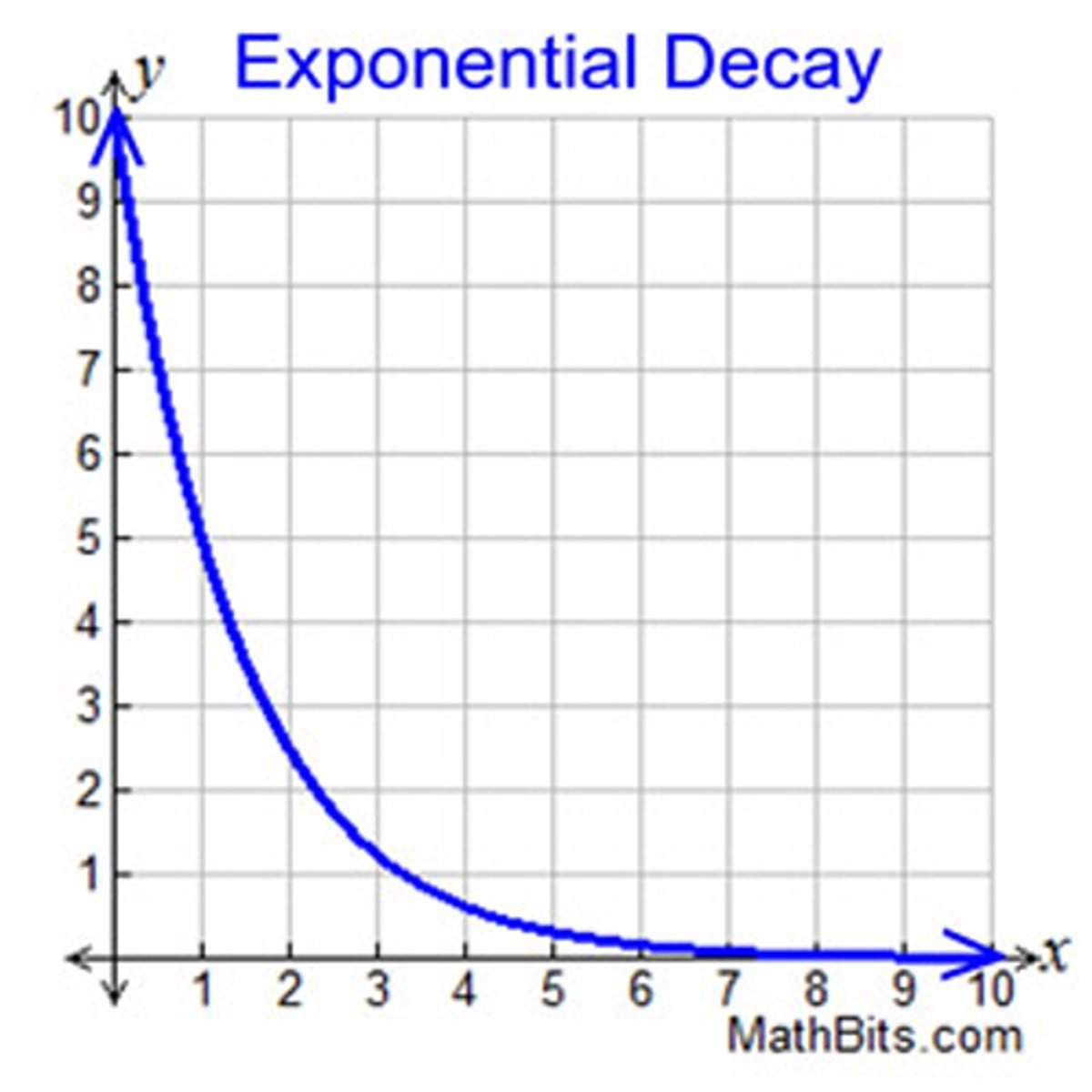
What is the constant-ratio property of exponential decay graphs? (2)

- This means that whenever the y-axis decreases by a certain proportion which takes place over a certain length of the x-axis.

- Each time the y-axis decreases by that same proportion, it will always take the same length on the x-axis.

What is the relation between capacitance and area? (1)

As the capacitance depends on the amount of electrons that can be stored on a plate, the capacitance is directly proportional to the area of the plate.

What is the relation between capacitance and separation of the plates? (2)

- The attraction between the plates depends on the distance, less distance means there is more attraction and less electrons can be stored on the plate.

- So the capacitance is inversely proportional to the separation of the plates.