Logarithm and Exponential Functions Unit 3 3.1-3.4

Review but hard

Hw assignment

around page #245

BOLD TERMS ARE SUPER IMPORTANT BOLD+ ITALIZIZE MOST IMPORTANT

3.1 Exponential functions and there graphs

2 functions we will study in this chapter

exponential functions and logarithmic functions.

These functions are examples of transcendental functions.

Definition of an Exponential function

The exponential function F with base A is denoted by

f(x)= a^x

where a>0, a≠1. and x is any real number

Why does base a have to be positive and cant be 0

Why the base a in f(x)=a^x must be positive for logs and exponential functions

Problem with a negative base:

• If a<0 then a^x can become exponents under 1

  • Example: (−2)^1/2 = sqaure root of -2 ​ → not a real number

1. Positive base works for all real exponents:

   • Any positive number raised to a real number is always real and positive.

   • Example: 2^1/2 sqrt 2

2. Summary:

   • Positive base ensures the function is defined for every real x.

   • Negative base breaks the function for fractional or irrational exponents.

If f(x)=0^x

1. For positive exponents (x>0):

   0^x=0

   ✅ This works fine.

2. For x = 0:

   0⁰ is undefined!

   ❌ There’s no universally agreed value for 0^0

3. For negative exponents x<0

   0^-1→ undefined!

a>0ensures the function is always positive

a≠1ensures the function actually changes with x

a≠0 avoids undefined values for negative and zero exponent

Evaluating Exponential Functions

a. f(x)=2^x x=-3.1. just plug in on calculator get .1166291

Just use calculator enclose fractional exponents in parenthesis

^{Graphs of Exponential Functions}

y=a^x

sketch graph of F(x)=2^x, G(x)=4^x

List the values in a table for each function Note that both graphs are increasing. Moreover, the graph of is increasing more rapidly than the graph of

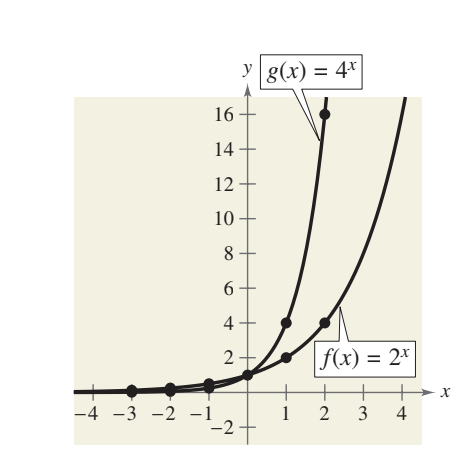
Graphs of Exponential Functions

y=a^-x

sketch graph of F(x)=2^-x, G(x)=4^-x

List the values in a table for each function. Note that both graphs are decreasing. Moreover, g(x) is decreasing more rapidly than f(x)

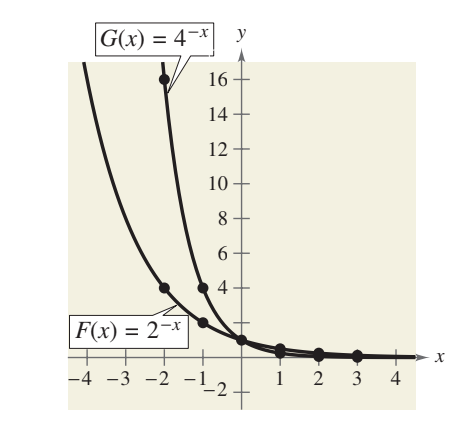
Comparing the 2 exponential functions

IMPORTANT

F(x)=2^-x= f(-x) and   G(x)=4^-x = g(-x) 

IT IS A REFLECTION OVER THE Y-axis 

SUPER IMPORTANT

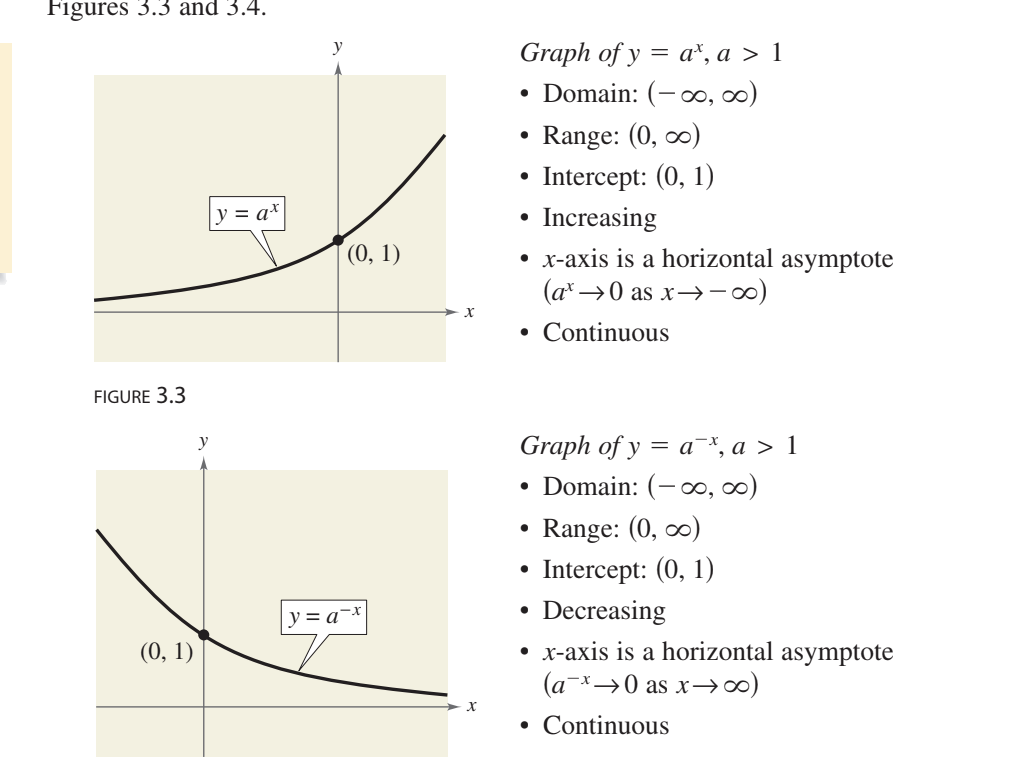
EXPONENTIAL FUNCTION GRAPHS OVERVIEW CHARACTERISTICS

range for both is (0,infinity) no negative range

FOR ALL EXPONENTIAL FUNCTIONS (0,1) ON IT

as x approaches negative infinity  y approaches 0 from above for positive

as x approaches infinity y approaches infinity for positive

One-To- One property EXPONENTIAL FUNCTIONS

and examples

The graphs both pass the horizontal line test so ONE-TO-ONE functions

SO can use ONE-TO-ONE PROPERTY TO SOLVE SIMPLE EXPONENTIAL EQUATIONS

for a>0 and a≠1 , a^x=a^y if and only if x=y

EXAMPLE

9=3^x+1 equals 3²=3^x+1 so x+1=2 so x=1

Transformations of EXPONENTIAL FUNCTIONS

Start with f(x)=3^x

SAME AS ALL OTHER FUNCTIONS

Shift asymptote with it

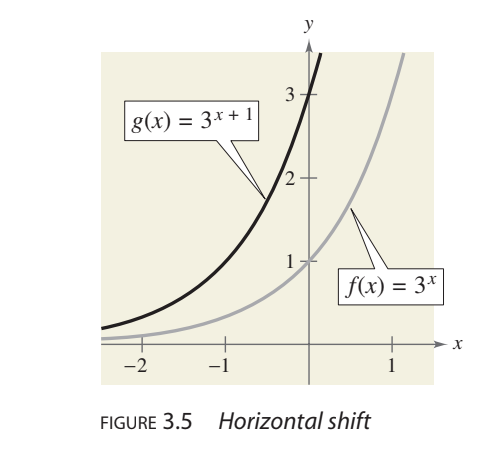
Horizontal shift

g(x)=3^x+1 = f(x+1) shift graph of f one unit to the left to get graph of g

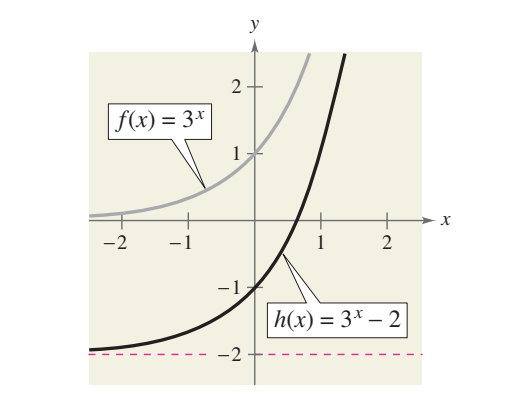
Vertical SHIFT

h(x)=3^x-2 = f(x) -2 shift graph of f 2 units down to get graph of h

Reflection over x-axis

k(x)=-3^x = -f(x) reflect f over x-axis to get graph of k

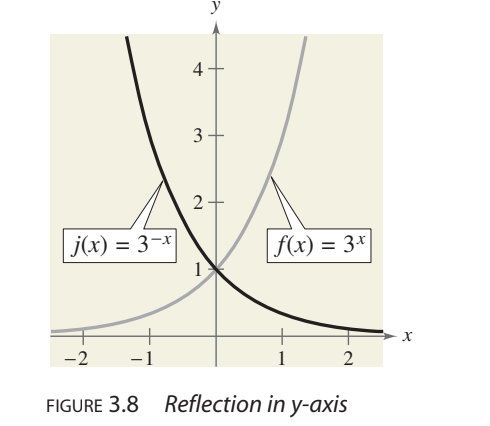
reflection over y-axis

j(x)=3^-x= f(-x) reflect f over y-axis to get j

Other shifts like vertical stretch and shrink and horizontal stretch and shrink are same thing as normal

Natural Base E

e is called the natural base. function f(x)= e^x called natural exponential function

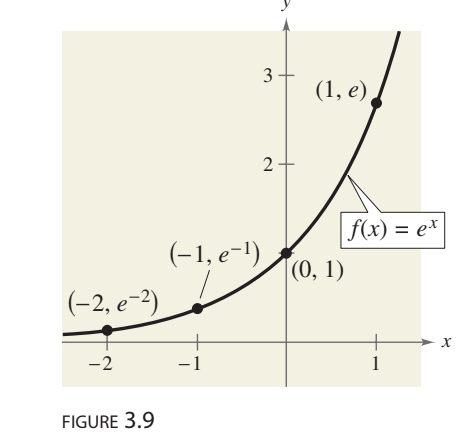
Evaluation natural Exponential Function

use calculator f(-2)=e^-2 plug in on calculator get .13533

Graphing Natural Exponential Functions

Sketch the graph f(x)=2e^.24x use graphing utility to plot points or

using what you know about exponential graph of y=a^x know that as a^x approaches 0 x approaches negative infinity and as y=a^x approaches infinity x approaches infinity and know that the x intercept is (2,0) and graph it.

3.2 Log functions and there graphs

Domain of Exponential Functions

Domain: (−∞,∞)

• Exponential functions are defined for all real numbers x.

• Example: f(x)=2^x→ any x works.

• Negative exponents are allowed because of the rule:

a^-x=1/a^x

Range of Exponential Functions

Range: (0,∞)

• The output is always positive, never zero or negative.

• The horizontal asymptote is y=0

• Because

• For negative x-values: a^-x=1/a^x which is greater than 0 

• For positive x-values: a^x>0

• So, no matter what x is, f(x)  is always greater than 0, never negative.

Intro what is LOG

that if a function is one-to-one—that is, if the function has the property that no h orizontal line intersects the graph of the function more than once—the function must have an inverse function.

By looking back at the graphs of the exponential functions introduced in Section 3.1, you will see that every function of the form y=a^x passes the Horizontal Line Test and therefore must have an inverse function.

This inverse function is called the logarithmic function with base a.

Inverse function properties

as we know inverse means reflect over y=x and also to solve for x you switch x and y

Definition of Log function with base a

for x>0, a>0 and a≠1 

y=log_ax if and only if x=a^y

The function given by f(x)=log_ax called  Log function with base a

Log form verus Exponential form

y=log_ax vs. x=a^y

Ex 1. Evaluating logs

ex. f(x)= log₂x x=32 = 5 because 2⁵=32

Common Log function

The logarithmic function with base 10 is called the common logarithmic function. It is denoted by or simply by log.

VERY IMPORTANT PROPERTIES OF LOGS MOST

PROOF OF Log_ax+log_ay=log_axy

PROOF OF Log_ax-log_ay=log_a(x/y)

PROOF OF Log_ax²=2log_a(x)

Example 3 using properties of Logs

ex. simplify log₄1. it is 0 using property 1

ex. simplify log_root7root7 it is 1 using property 2

Example 4 using one-to-one property

ex. log₃x=log₃12 x=12

ex. log(2x+1)=log(x). x=-1

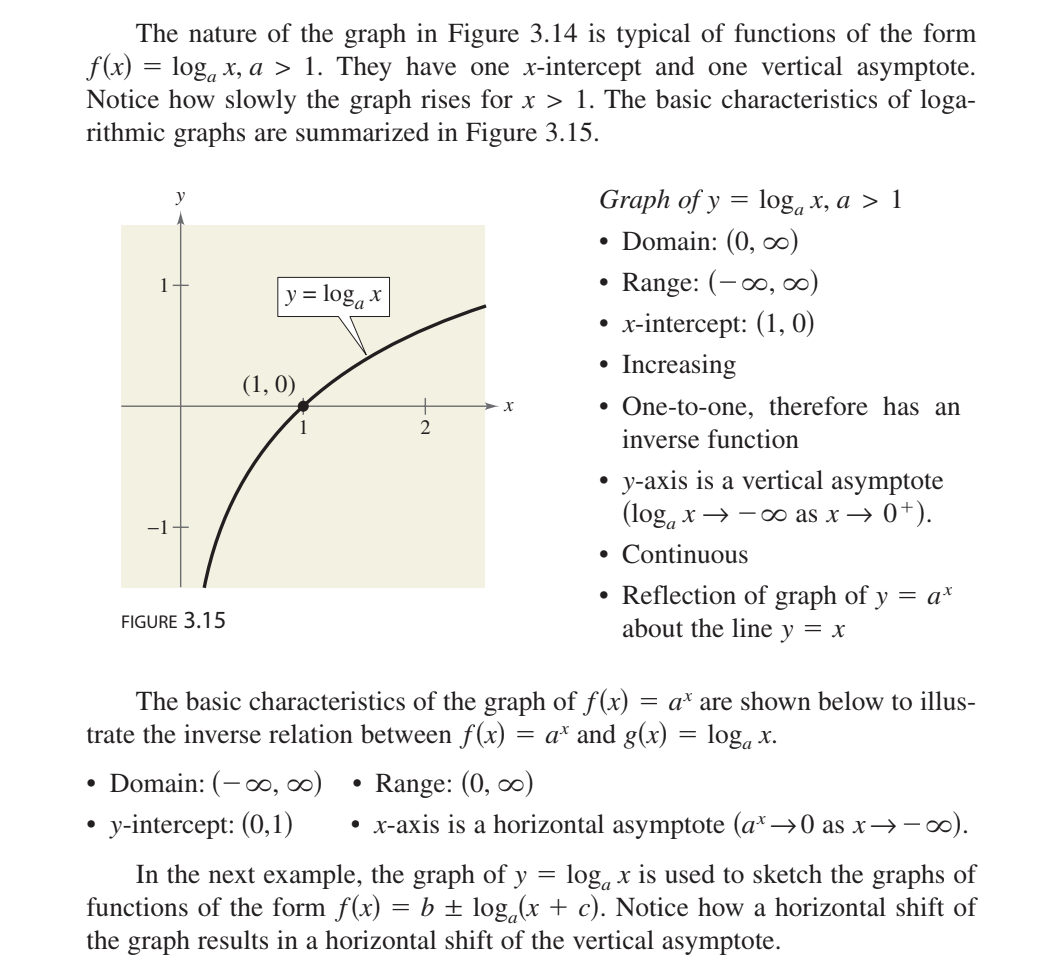
GRAPHS OF LOG FUNCTIONS 

to sketch the  graph of y=log_ax use fact that the graphs of inverse

functions are reflections of each other in the line y=x

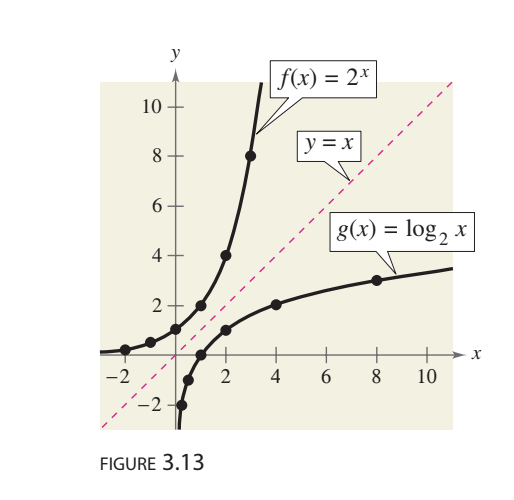
Example 5 Graphs of Exp and LOG FUNCTIONS

f(x)=2^x. g(x) y=log₂(x)

For f(x) construct a table of values. By plotting these points and con-

necting them with a smooth curve

Because g(x) is the inverse function of the graph of f(x) graph of g obtained by plotting the opposite points of

Example 6 Sketching the Graph of a Logarithmic Function

Sketch the graph of the common logarithmic function f(x)=log(x)  Identify the vertical asymptote.

plot points in a table of values x=1 will always be 0 

X- INTERCEPT FOR ALL LOG FUNCTION GRAPHS WITH NO TRANSFORMATIONS (1,0) then use knowledge like x=10 y=1 and x=1/10 y=-1 

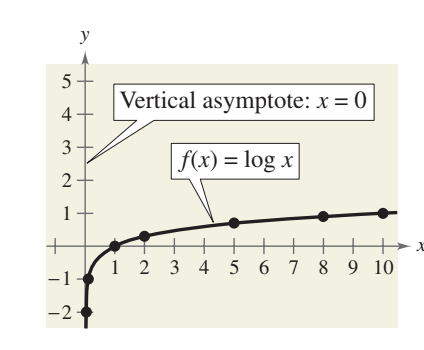
graph of y=log_a(x) CHARACTERISTICS 

as x approaches 0 from above y approaches negative infinity 

as x approaches infinity y approaches infinity

TRANSFORMATIONS OF LOG FUNCTIONS

SAME AS EXPONENTIAL

Natural Log Function

natural exponential function f(x)=e^x has an inverse called natural log

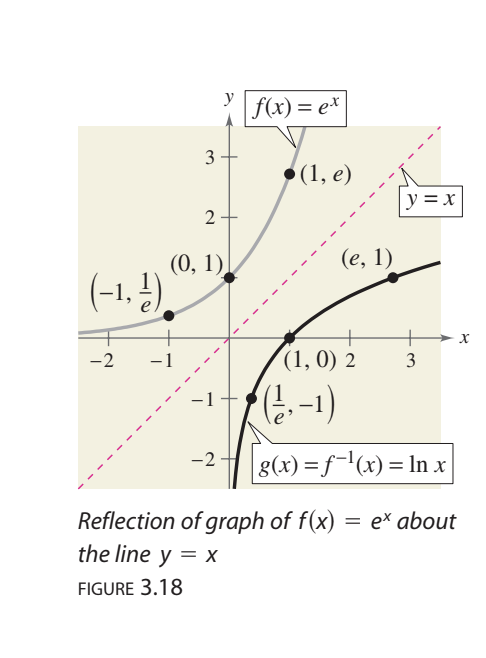
Natural log defined 

f(x)=log_e(x)=lnx, x>0

Properties of Natural logs  SAME AS PROPERTIES OF LOGS 

Domain OF LOG FUNCTIONS

• Definition: log⁡_a(x)=y is a^y=x

• The exponential a^y is always positive, so x must also be positive.

• You cannot take the log of 0 or a negative number because there is no real number yyy that satisfies ay=0a^y = 0ay=0 or ay<0a^y < 0ay<0.

• ✅ Domain: (0,∞)

Range OF LOG FUNCTIONS

• Logarithm outputs any real number because a^y can take any positive number.

• For any positive x, there is some y such that a^y=x

• This means y=log⁡_a(x)  can be very negative, zero, or very positive.

• ✅ Range: (−∞,∞)

Finding domain’s example

1. h(x)=lnx²

it would be defined only if x² is greater than 0

3.3 PROPERTIES OF LOGS

Change of Base

might need to evaluate logs of other bases than 10 and e so use change of Base formula

Example 1 Changing base using common logs

a. log₄25 = log(25)/log(4) and then use calc

b. log₂12 =log(12)/log(2) and then use calc

MOST IMPORTANT THING SO FAR

know that log_a(x) is the inverse of the exponential function with base a so properties of exponents should have corresponding ones with logs.

Example Using properties of Logs

1. log6 = log 2 + log 3

2. log₅ cube root5 = log5 5 ^1/3 = 1/3

Rewriting Logarithmic Expressions

The properties of logarithms are useful for rewriting logarithmic expressions in forms that simplify the operations of algebra. This is true because these properties convert complicated products, quotients, and exponential forms into simpler sums, differences, and products, respectively.

Example 5 Expanding Log expressions

1. log₄5 x ³y- is log₄(5)+3log₄x+log₄y

2. ln root (3x- 5)/7 is 1/2ln(3x-5) - ln(7)

Example 6 Condensing Log expressions 

1/2log(x)+3 log(x+1)

log(root x (x+1)³ )

1/3 [log₂x + log₂(x+1)}

log₂ cube root x(x+1)

3.4 Exponential and Log equations

So far in this chapter, have studied the definitions, graphs, and properties of exponential and logarithmic functions. In this section, you will study procedures for solving equations involving these exponential and logarithmic functions.

There are two basic strategies for solving exponential or logarithmic

equations.

The first is based on the One-to-One Properties and was used to solve

simple exponential and logarithmic equations in Sections 3.1 and 3.2

The second is based on the inverse properties. for a>0 the following

properties are true for all x and y for which log_ax and log_ay are defined.

One to one properties Solving equations

a^x=a^y IFF x=y

log_ax=log_ay IFF x=y

Inverse properties Solving equations

a^log_ax=x

log_aa^x=x

Example 1 Solving simple equations

1. 2^x=32. rewrite 2^x=2⁵. x=5 because of 1to 1

2. e^x=7 ln e^x= ln7. x=ln7 because of inverse

Strategies for Solving Exp and Log equations

Example 2 Solving Exponential equations

1. e^-xsquared = e^-3x-4 use one to one and factor and get x=4 and x=-1 

2. 3(2^x)=42 divide each side by 3 and then log₂ both sides and get log₂14

Example 3 Solving an exponential Equation

1. e^x+5=60 subtract 5 from both sides and then natural log both sides to get x = ln 55

2. 2(3^2t-5)-4=11 add 4 to both sides and then divide both sides by 2 then log 3 both sides and then solve and get t=1/2 log₃(15/2) + 5/2

Example 5 solving quadratic exponential equation

Solving Log equations

to solve a log equation, you can write it in exponetial form

1⃣ ln⁡(x)=3
Exponentiate both sides (base e):

e^ln(x)=e³. ⇒x=e³

Exponentiating

Exponentiating means raising both sides of an equation to the base of the logarithm to “undo” the log.
It’s the inverse operation of taking a logarithm.

If

log⁡_a(x)=y  then exponentiating gives

a^y=x.

Why it works:
The logarithm and exponential functions are inverses:

a^log_ax=x. and log⁡_a(a^x)=x.

---

Examples:

1⃣ ln⁡(x)=3
Exponentiate both sides (base e):

e^ln(x)=e³3 ⇒x=e³

Example 6 Solving Log equations

Ex 7 Solving a Logarithmic Equation

Ex 8 solving a Log equation

Checking for Extraneous Solutions

Because the domain of a logarithmic function generally does not include all

real numbers, you should be sure to check for extraneous solutions of logarithmic

equations.

An extraneous solution is a number that appears valid algebraically but does not satisfy the original equation, often because it makes a logarithm undefined.

Why It Happens:
Logarithms are only defined for positive arguments.
So if solving gives you an x that makes any log term ≤ 0, that solution must be rejected.

Steps to Check:

1⃣ Solve the equation normally (using log rules or exponentiating).
2⃣ Substitute each solution back into the original logarithmic expression.
3⃣ Reject any value that makes a log’s input ≤ 0.

Example:

log⁡(x-2)+log(x+1)=log(3)

Solve x=2 and x=-1

check

x=-1 invalid  because cannot have log(-3)

Ex 9 checking for extraneous solutions