Matrices
5.0(7)
5.0(7)
Card Sorting
1/22
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
23 Terms
1
New cards
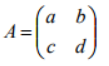
how to find the determinant
ad-bc
2
New cards
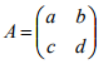
how to find the inverse of 2x2 matrix
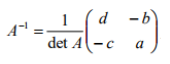
3
New cards
what is the minor of an element
the determinant of the matrix obtained by deleting the row and column in which that element lies
4
New cards
when is a matrix singular and what does this mean?
when detM=0, so this matrix doesn't have an inverse
5
New cards
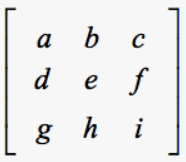
how to find the determinant
a(minor of a) -b(minor of b) +c(minor of c)
6
New cards
what is the transpose of a matrix?
changing the columns into rows, and vice versa
7
New cards
acronym and steps to inverse the 3x3 matrix A
Driving Monkeys Can’t Travel Fast
detA, matrix of minors, matrix of cofactors, transpose, apply the formula
detA, matrix of minors, matrix of cofactors, transpose, apply the formula
8
New cards
how to form the matrix of cofactors
switch the sides' signs, keep the corners constant (and the middle)
9
New cards
the final formula in finding the inverse of a 3x3 matrix
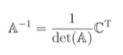
10
New cards
how to form the 3x3 matrix in the simultaneous equations method
each row is the coefficients of x, y and z in each equation
11
New cards
how to solve matrix simultaneous equations
(matrix of coefficients)\*(x,y,z matrix)=(matrix of answers to sim.eqs)
12
New cards
when do the planes meet at a single point
when the determinant is __**not**__ 0
13
New cards
when do the planes form a sheaf
det=0, reduced to two equations which are consistent, the three equations aren’t multiples of each other
14
New cards
when are the planes the same plane
all three **equations** are multiples of each other
15
New cards
when do the planes form a prism
det=0, when reduced to two equations they are inconsistent, no rows of the matrix are multiples of each other
16
New cards
when are only two planes parallel
when **only** two rows of the matrix are multiples of each other
17
New cards
when are all the planes parallel
when all rows of the matrix are multiples of each other, but __**not**__ the equations
18
New cards
what does the determinant of a transformation matrix represent
area scale factor
19
New cards
a rotation of A about the x axis
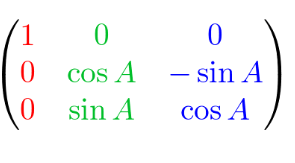
20
New cards
a rotation of θ about the y axis
\
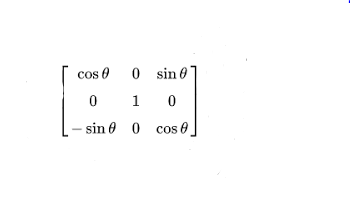
21
New cards
a rotation of C about the z axis
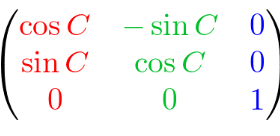
22
New cards
det(AB)=
(detA)(detB)
23
New cards
(AB)⁻¹=
B⁻¹A⁻¹ (think of order of geometric transformations)