SAT MATH SHTUFF

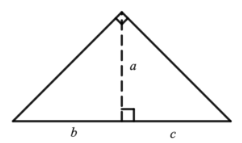
a²=bc

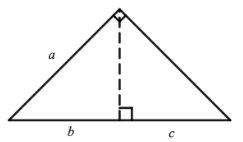
a²=b(b+c)

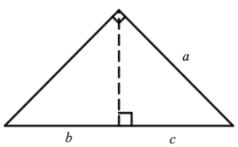
a²=c(b+c)

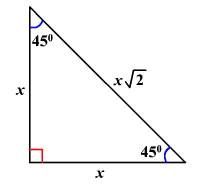
45-45-90

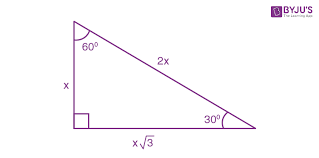
30-60-90

If two parallel lines are cut by a transversal line…..

then the corresponding angles are congruent.

If two lines are cut by a transversal line, and corresponding angles are congruent

then the lines are parallel.

If two parallel lines are cut by a transversal line, then the alt….

ernate interior angles are congruent.

If two lines are cut by a transversal line, and the alternate interior angles are congruent,

then the lines are parallel.

If two lines are cut by a transversal line, and the consecutive (same side) ) interior angles are supplementary,

then the lines are parallel

The sum of the measures of the interior angles of a triangle is

180 degrees

The measure of an exterior angle is equal to the sum of

the two non-adjacent (remote) interior angles

The interior angles of a polygon with n sides always sum up to

180(n-2)

The interior angles of a polygon with n sides always sum up to —- degrees

360

For a regular polygon, the measure of an interior angle is

(180(n-2))/n

For a regular polygon, the measure of an exterior angle is

360/n

The length of one side of a triangle is between

the difference of the two other sides and the sum of the two other sides.

circle

perimeter: 2 (pi) {r}

area: (pi) r²

parallelogram

perimeter: 2(l+w)

area: b(h)

Trapezoid with bases b₁ and b₂ and height h

perimeter: sum of sides

area: {(b₁ + b₂ ) / 2} (h)

Rhombus with diagonals d₁ and d₂ and side s

perimeter: 4s

area: (d₁ d₂) / 2

Cube

surface area: 6s²

volume: s³

Sphere

surface area: 4 (pi) r²

volume: (4/3) (pi) r³

cylinder

surface area: 2 (pi) {r} (h) + (pi) r²

volume: 1/3 (pi) (r²) (h)

cone (w slant height s)

surface area: (pi) {r} (s) + (pi) r²

volume: 1/3 (pi) (r²) (h)

rectangular prism

surface area: 2(lw + wh + hl)

volume: lwh

pyramid w base B and height h

surface area: ———

volume: 1/3 (B) (h)

triangular prism w base B and height h

surface area: ———

volume: Bh

Two figures are similar if

• they have the same shape.

• their corresponding angles are equal.

• the ratio of their sides are the same.

If two plane figures are similar with a scale factor of a/b, then their perimeters

are also in the ratio of a/b

If two plane figures are similar with a scale factor of a/b, then their areas

are also in a ratio of (a/b)²

If two solids are similar with a scale factor of a/b, then the surface areas

are in a ratio of (a/b)²

if two solids are similar with a scale factor of a/b, then the volumes

are in a ratio of (a/b)³

SSS equivilancy

side side side - if all three sides are the same length, then the triangles are congruent.

SAS

side angle side - if two triangles have two sides the same length, and the angle between the two sides has the same measure in both triangles, then the triangles are congruent.

ASA

angle side angle - if two triangles have two angles the same, and the side that connects the two angles is the same length in both triangles, then the triangles are congruent.

AAS

angle angle side - if two triangles have two angles that are the same, and the side opposite to one of the angles has the same length in both triangles, then the triangles are congruent.

HL

hypotenuse leg - if there are two right triangles where the hypothenuse is the same length in both and one other side is the same length in both triangles then the triangles are congruent.

Two triangles are similar if:

• all of their angles are equal; and

• corresponding sides are in the same ratio.

AA

angle angle - if two triangles have two angles that are the same, then the triangles are similar.

SAS

side angle side - this doesn't mean the sides are the same length, it means the ratio of the sides is the same.

SSS ratio

side side side - if the ratio of all three sides are the same, then the triangles are similar.

Pythagorean triple: 3,4 &….

5

Pythagorean triple: 5,12, &…

13

Pythagorean triple: 7, 24, &…

25

Pythagorean triple: 8, 15, &…

17

If two angles, A and B are complementary, then

sin A= cos B & sin B= cos A

if sin A = cos B or sin B= cos A, then

the two angles (A & B) are complementary.

for right triangle ABC, where C is the right angle,

sin A= cos B & cos A= sin B

360 degrees = ___ radians

2pi

degrees —> radians

multiply the number of degrees by pi/180

radians —> degrees

multiply the number of radians by 180/pi

Slope-intercept form

y=mx+b

Point-Slope form

y - y₁ = m(x - x₁)

standard form

Ax + By = C

if equation is in standard form use ____ to find slope

-A/B

if equation is in standard form use ____ to find y intercept

C/B

to find x intercept…

set y=0

to find y intercept….

set x=0

the equation of a horizontal line is…

y=b, where b is a constant and the y intercept

the slope of a vertical line is…

undefined

the slope of a horizontal line is…

0

the equation of a vertical line is…

x=a where a is a constant and the x intercept of the line

two lines are perpendicular id they have…

negative (opposite) reciprocal slopes

For up/down shift of a function, the constant k

is added/subtracted at the end of the function

For right/left shift of a function,

x is replaced by x - k or x + k

To find the center of a circle when the end points of a diameter are given, we use Midpoint Formula.

where (x₁, y₁) and (x₂, y₂) are the endpoints of the diameter.

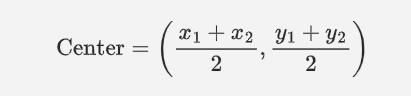
To find the radius of a circle when the end points of a diameter are given, we use Distance Formula.

where (x₁, y₁) and (x₂, y₂) are the endpoints of the diameter.

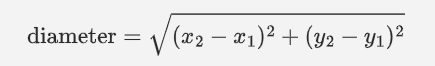
To quickly find the center without completing the square,

cut the x and y coefficients into half and change the sign.

The point where tangent meets the circle is called…

point of tangency

The tangent is….

perpendicular to the radius of the circle at the point of tangency.

A central angle is an angle….

whose vertex is the center of a circle and whose sides are radii intersecting the circle in two distinct points.

equation of a circle

(x - a)² + (y + b)² = r²