Chapter 1: Electrostatics

What is the triboelectric effect?

Charges (typically electrons) are transferred between materials when in contact with one another, and are retained when the materials are separated. Friction increases the contact between the surfaces, thereby increasing the triboelectric effect.

What is the principle of charge conservation?

The total charge of any system is always conserved. When charges are created, equal amounts of opposite charges are produced. Charging of objects occurs through transfer of charges.

Explain Coulomb’s force equation

\overrightarrow{F}=\frac{1}{4\pi \epsilon_0} \frac{q_1q_2}{r²}\widehat{r}

\overrightarrow{F}= electrostatic force

\frac{1}{4 \pi \epsilon_0} = Coulomb’s constant 9×10^9 Nm²C^{-2}

q_1 and q_2 = magnitude of the two changes in Coulombs

r = distance between the two charges, in metres

\widehat{r} = unit vector pointing from q_1 to q_2

What does the statement that electrostatic forces are conservative mean?

The next force acting on a single charge Q due to a collection of other charges q_i is the vectorial sum of individual forces (not magnitudes) acting on it.

\overrightarrow{F}_{net}=\Sigma\overrightarrow{F}_i =\frac{Q}{4 \pi \epsilon_0} \Sigma \frac{q_i}{r_i²} \widehat{r}_i

What is the superposition principle of forces?

The net response caused by two or more stimuli is the sum of the responses caused by each individual stimulus.

What is the electric field?

The electric force acting on a charge, per unit charge.

Alternatively, they can be thought of as sources of electric forces instead. That is, when a charge Q is placed into an electric field \overrightarrow{E}, it will experience an electric force \overrightarrow{F}=Q \overrightarrow{E}. All charges produce electric fields around themselves.

What is the equation for the electric field produced around a point charge?

\overrightarrow{E}(\overrightarrow{r})=\frac{1}{4 \pi \epsilon_0} \frac{q}{r²} \widehat{r} where \overrightarrow{r} is the vector connecting the charge to the point in space where the electric field is being observed.

How are electric fields drawn?

Electric fields of positive charges always point away from them, whilst the electric fields of negative charges always point towards them, regardless of the test charge.

What is the equation for the net electric field produced by a collection of charges q_i at some observation point in space, P?

\overrightarrow{E}_{net}=\Sigma \overrightarrow{E}_i= \frac{1}{4 \pi \epsilon_0} \Sigma \frac{q_i}{r_i²} \widehat{r}_i where r_i is the distance between the source charge and the observation point

What are electric fields measured in?

Volts per metre or Newtons per Coulomb

What is the equation for an electric field generated by an extended charged object at some observation point?

\overrightarrow{E}_{net}=\frac{1}{4 \pi \epsilon_0} \int \frac{\widehat{r}}{r²} dq

where dq = charge of the infinitesimally small segment on the object, r = distance from this segment to the observation point, \hat{r} = unit vector pointing from the segment to the observation point. These expressions as a function of some space parameter must be obtained in order to be able to perform the integration over the object.

What is dq expressed as?

dq is expressed in terms of charge density of the object.

For 1D objects. dq is line charge density, \lambda, C/m, measures charge per unit length

For 2D objects, dq is surface charge density, \sigma, C/m², measures charge per unit area

For 3D objects, dq is volume charge density, \rho, C/m³, measures charge per unit volume

What are charge densities like for uniformly and non-uniformly charged objects?

Charge densities can be functions of space for non-uniformly charged objects, but for uniformly charged objects they are constants.

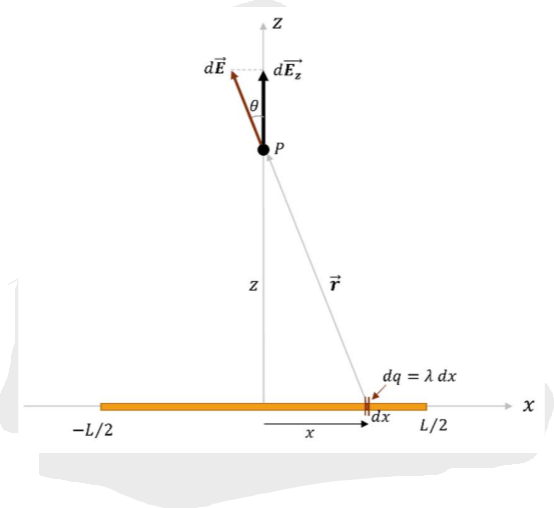
Derive an expression for the electric field of rod of length L, charged uniformly to hold a total charge of Q, at observation point P located directly above the midpoint of the rod and a distance z away from it.

Since the rod is uniformly charged, the charge density is constant and equal to \lambda=\frac QL . A small segment of the rod of infinitesimally small length dL will hold a charge of dq=\lambda dL, but this can be written as dq=\lambda dx

r from dq can be expressed as Pythagoras: r=\frac{z}{\cos \theta}=z \sec \theta. The direction of unit vector \hat{r} is therefore \hat{r}=-\sin \theta \hat{x}+\cos \theta \hat{z}.

Convert dx into a function involving the same parameters: x=z\tan \theta \rightarrow dx=z \sec² \theta d\theta

Applying Coulomb’s law: d \hat{E}=\frac{1}{4 \pi \epsilon_0} \frac{dq}{r²} \hat{r}=\frac{\lambda dx}{z² \sec² \theta}(-\sin \theta \hat{x}+\cos \theta \hat{z})= \frac{\lambda}{4 \pi \epsilon_0 z}(-\sin \theta \hat{x}+\cos \theta \hat{x}) d\theta

To find the total electric field produced by the rod at P, integrate with respect to \theta between \theta_L and -\theta_L: \overrightarrow{E}_P=\frac{\lambda}{4 \pi \epsilon_0 z} \int (-sin \theta \hat{x}+\cos \theta \hat{z})d\theta = \frac{1}{4 \pi \epsilon_0} \frac{2 \lambda \sin \theta_L}{z} \hat{z}

\sin \theta_L = \frac{x_L}{r_L}=\frac{L/2}{\sqrt{z²+(L/2)²}} \hat{z}

\overrightarrow{E}_P=\frac{1}{4 \pi \epsilon_0} \frac{Q}{z\sqrt{z²+(L/2)²}} \hat{z}

What happens in the limiting cases of this expression: \overrightarrow{E}_P=\frac{1}{4 \pi \epsilon_0} \frac{Q}{z\sqrt{z²+(L/2)²}} \hat{z} ?

When L«z, i.e. when the rod is tiny compared to the observation distance, the expression reduces to the expression for the electric field of a point charge.

When L»z, i.e. when the rod is infinite, the expression simplifies to a case when the electric field is distance-dependant and varies as 1/r.

What are two ways in which electric field lines can be drawn?

• Draw a set of electric field vectors at different points around the object, with the lengths and directions indicating the magnitude and direction of the electric field

• Draw continuous electric field lines where the arrows on the lines indicate the direction and the density of the field lines indicate the magnitude

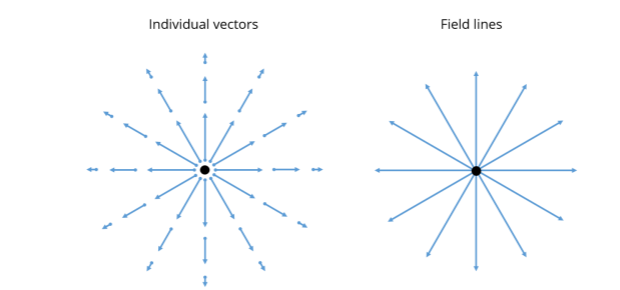
What are the five rules of drawing electric field lines?

• Field lines begin on positive charges and end on negative charges

• Field lines do not cross

• Field lines are normal to surfaces

• Field line density is proportional to the charge

• Field line density at the surface is proportional to the surface curvature i.e. local magnitude in the local density of the lines

What is an electric dipole?

A pair of opposite charges of equal magnitudes separated by some distance d.

What is an electric dipole moment, \overrightarrow{p}?

A vector quantity whose magnitude is equal to the product of the charges’ magnitude and their separation, and whose direction is from the negative charge and towards the positive charge.

|\overrightarrow{p}| = qd

What are some examples of electric dipoles?

• Many molecules composed from different atoms are in fact dipoles due to unequal sharing of electrons

• In most cases, EM waves are generated by oscillating diploes, be that by a physical antenna or by excited molecules

• Responsible for anything that produces light

How is the electric field of diploes different to the electric field of regularly charged objects?

• Electric field dies very quickly away from dipoles as E \propto 1/r³

• The electric field magnitude is proportional to the electric diploe moment

• If the diploes are oscillating, the electric field will also oscillate, producing magnetic fields

Summarise the results for electric field dependencies on distance, in the far-away limit.

• Dipole: \propto 1/r³

• Discrete charges: \propto 1/r²

• Line of charge: \propto 1/r

• Plane of charge E-field is constant

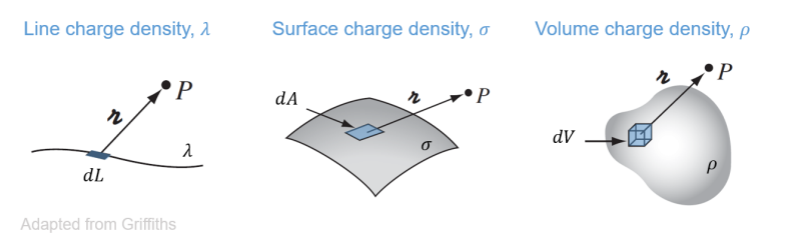
What is electric flux?

Electric flux is a mathematical construct that can be defined as a measure of electric field crossing a surface normally.

What is the relationship between electric flux, electric field strength and the area of the plane surface?

\Phi_E=\overrightarrow{E}*\overrightarrow{A}

They are all proportional to each other

What is the direction of \overrightarrow{A}?

The direction is perpendicular to the plane of the surface

What are the units of electric flux?

Newton metres-squared per Coulomb, Nm²C^{-1}

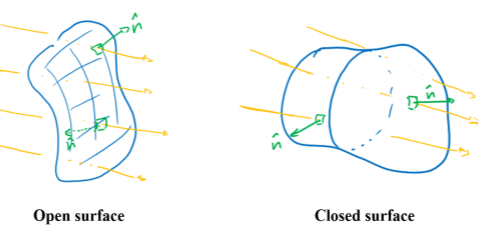
What is an open surface?

A surface that does not enclose a volume e.g. a flat sheet, rectangle - in reflection of this, there will generally be two possible directions for the normal vector to the surface

What is a closed surface?

A surface which encloses a volume and is characterised by having inner and outer sides. The direction of the normal vector is conventionally described as the outward direction.

What is the direction of the normal vector for open and closed surfaces and how does this affect flux?

• Open: The flux is positive if it is out of the object and negative if it into the object

• Closed: outwards flux is always positive

What does Gauss’ law state?

Gauss’ law for electric fields states that the electric flux through a closed surface is proportional to the charge enclosed by it.

What is the electric field of a sphere treated as?

For a uniform sphere, the electric field outside is like that of a point charge, and the electric field inside depends on the charge enclosed within the radius.

What is the electric field of a cylinder treated as?

Everything is centre-symmetric

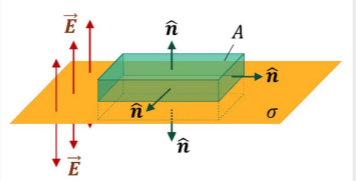
Use Gauss’ law to develop an expression for the electric field due to an infinite and uniformly charged planar sheet.

Consider an infinite (as edges cause flares in electric fields) plane sheet of charge density \sigma. By symmetry, \overrightarrow E produced will be uniform and normal to the sheet surface. the appropriate Gaussian surface will have all its surfaces either parallel or perpendicular to the field lines. A square pillbox can be used: an imaginary box of height h and top/bottom surface areas A, with the top and bottom lying parallel to the sheet.

The total charge enclosed is Q_{encl}=\sigma *A

The total flux out of the pillbox can be found by summing fluxes out of the individual sides. For the top and bottom surfaces, the normal to the area vectors is parallel to the electric field (\overrightarrow E*\overrightarrow A = EA) and the side surfaces are perpendicular (\overrightarrow E * \overrightarrow A = 0).

Therefore, \Phi_E=2EA \rightarrow 2EA=\frac{\sigma A}{\epsilon_0} \rightarrow E = \frac{\sigma}{2 \epsilon_0}

How can Gauss’ law derive Coulomb’s law?

Consider a sphere as a point charge, therefore the electric field produced by the charge will then be the same everywhere on the Gaussian surface i.e. E = constant.

The flux out of the Gaussian sphere is then: \Phi_E=E \int dA \rightarrow 4 \pi r²E.

4 \pi r² E= \frac{Q}{\epsilon_0} \rightarrow E = \frac{1}{4 \pi \epsilon_0} \frac{Q}{r²}

How does a dipole act in a uniform electric field?

A dipole will experience a torque acting on it, as a result of which it will rotate around its centre of mass until it is aligned with the electric field.

What is electrostatic equilibrium?

Charges inside charged objects will each generate their own electric fields, exerting forces on all other charges and causing charge redistribution. They continue doing so until a quasi-equilibrium is achieved, termed electrostatic equilibrium.

What is electrostatic equilibrium like for conductors?

Electrostatic equilibrium is characterized by all charges being confined to the outer surfaces, zero internal electric fields and surface fields of \sigma/\epsilon_0.

Describe the process of a conducting uniform sphere reaching electrostatic equilibrium.

• The moment just after the charge injection: the electric field drives the charges radially outward which changes the electric field distribution throughout the sphere

• This process continues until all of the charge is on the surface

• Electrostatic equilibrium is reached: the electric field inside is 0 and all the charge is on the outer surface

What is electrostatic equilibrium like for insulators?

Electrostatic equilibrium is characterized by a partial redistribution of charges and a partial reduction of the internal electric field.

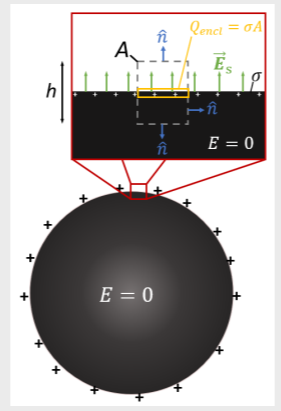
Calculate the magnitude of the electric field just outside the surface of a charged conductor at electrostatic equilibrium.

To find the electric field just outside the surface, consider just a tiny element of it.

Draw a small pillbox through our tiny conductor element, of height h and top surface area A, so that its top surface is just above the conductor and the bottom surface is well into the conductor volume, where E = 0.

EA = \frac{\sigma A}{\epsilon_0} \rightarrow E = \frac{\sigma}{\epsilon_0}

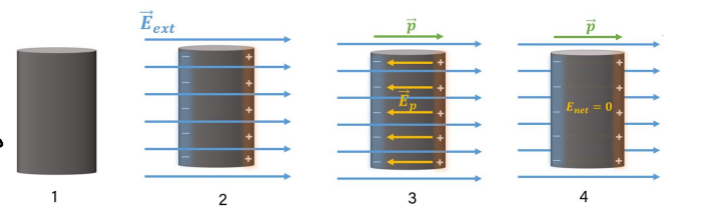
What does it mean when an object is polarised?

When neutral materials are subjected to external electric fields, the constituent charges (positive atomic cores and electrons) will experience electric forces. For both conductors and insulators, this results in accumulation of equal and opposite charges on opposite sides of the object, although the extent to which this happens differs between the two. In both cases then, the object is said to be polarized by external electric fields, via a process referred to as induction.

What is the effect of induction when placing a charged object inside an electric field and how does it affect the overall electric field?

The result of induction is the establishment of an electric dipole across the object, which generates its own electric field. The direction of this electric field is opposite to that of the external field, and so it acts to reduce the internal electric field inside the object.

What does the polarisation of a conductor look like?

For conductors, the electrons migrate throughout the object until the internal electric field is non-zero, resulting in larger dipole moments and consequently smaller electric fields. At electrostatic equilibrium, the electric field inside a neutral conductor is zero.

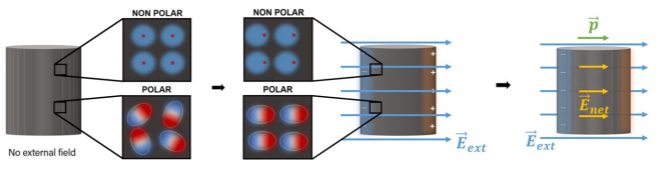
What does the polarisation of an insulator look like?

For insulators, less diploes are induced, which results in a partial cancellation of the internal electric field inside the dielectric material. The degree to which the internal electric field is reduced compared to the applied field, is characterized by one of the three material constants: \epsilon_r, \chi_e, \epsilon

What do the symbols \epsilon_r, \chi_e, \epsilon mean in the context of material constants?

\epsilon_r = dielectric constant, \epsilon_r = E_{vaccum}/E_{dialectric}

\chi_e = electric susceptibility, \chi_e=\epsilon_r - 1

\epsilon = electric permittivity, \epsilon=\epsilon_0*\epsilon_r

What is the equation for the net electric field using material constants \epsilon_r, \chi_e, \epsilon ?

\overrightarrow{E_{net}}=\frac{1}{\epsilon_0 \chi_e}

\frac{d\overrightarrow \rho}{dV}=\frac{1}{\epsilon_0 \chi_e} \overrightarrow \rho where \frac{d\overrightarrow \rho}{dV} is the density of dipoles induced and \overrightarrow \rho is the polarisation vector

How should this reduction of the electric field be accounted for in the equations for dielectrics?

Use \epsilon instead of \epsilon_0

What is electric potential energy?

Electric potential energy (Joules, J) of a charge at some point in space measures the work done against the electric force to bring this charge from infinity to that point.

What is the equation for electric potential energy?

U_P=-q \int \overrightarrow E . d\overrightarrow L where the integral ranges from infinity to that point

How can the change in electric potential energy be calculated for a uniform electric field?

\Delta U=-q\overrightarrow E . \overrightarrow L

What is the best way to calculate electric potential energy?

Since electric forces are conservative, the change in the potential energy in moving a charge does not depend on the path taken. When performing calculations, therefore, it is often convenient to choose a path that aligns itself with an electric field line (allowing you to drop the vector notation).

What is electric potential?

The electric potential (V ) at a point in space is the work done against the electric force in bringing a unit charge from infinity to that point. It measures the electric potential energy per unit charge.

What does equipotential mean?

A charge moves perpendicular to the electric field lines and so no work is done when moving between them. The initial and final stages are symmetrically equivalent.

What is the equation for the electric potential at distance r away from a point charge?

V[r]=\frac{1}{4 \pi \epsilon} \frac{q}{r}

How can the electric potential due to a continuous distribution of charges can be obtained?

V[r]=\frac{1}{4 \pi \epsilon} \int \frac{dq}{r}

How to find the electric potential for highly symmetric continuous distributions?

Use Coulomb’s or Gauss’s law to find E(r)

2. Integrate E(r) from infinity to r: V (r) = - \int \overrightarrow{E}[r] .d \overrightarrow r