Graphs

Path

Walk with no repeated edges.

Cycle

Closed walk with no repeated edges.

Connected Graph

Graph with a path between every pair of vertices.

Tree

Connected & does not contain a cycle.

Forest

Graph with no cycle, each component is a tree.

Euler Trail

Trail where every edge appears once, exactly 2 vertices of odd degree.

Euler Circuit

Circuit where every edge appears once.

Hamiltonian Path

Path containing every vertex.

Hamiltonian Cycle

Cycle containing every vertex.

Spanning Tree

Subgraph that spans another graph.

Articulation Point

A vertex whose removal increases the number of connected components.

Σ deg(v) = 2|E|.

Degree Sum Formula

V = E + 1

Tree Vertex Formula

V = E + k

Forest Vertex Formula

V - E + F = 2.

Euler's Formula for Planar Graphs

Graph Isomorphism

Two graphs that can be transformed into each other by renaming vertices.

Walk

Sequence of vertices and edges where each edge is incident with the vertex before and after it. A walk may repeat vertices and edges.

Trail

Type of walk in which no edge is repeated, but vertices may be repeated.

Planar Graph

Graph that can be drawn on a plane without any edges crossing each other.

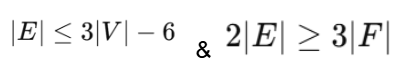
Bound for number of edges (Planar Graphs)