Multivariable Calculus – Lecture #1 Notes

R3, Intro to Vectors, Coordinate-free vector proofs, Spheres

vector subtraction: v - w, think of it as _____

v + (-w)

Position vector

Initial point at origin, terminal point at P(v1, v2)

Denoted as ____

〈v1, v2〉

Translating vector with initial point P1(x1, y1) and terminal point P2(x2, y2) into position vector

〈x2-x1, y2-y1〉

Slope of vector

y2-y1 / x2-x1

or v2/v1

Vector equality: must have same magnitude and direction

Find _____ for both and see if they’re the same

position vector

Multiplying by scalar: c * v = _____

Can change ____ or _____ of vector

scalar multiples are ____

〈c * v1, c * v2〉

length, reverse direction

parallel

unit vectors: vectors w/ length of 1

û = ____

v/|v|

IMPORTANT: vectors can be defined by magnitude * direction or unit vector

Denoted as _____

v= |v| * û

Standard basis vectors

î = x-direction,〈1,0〉

ĵ = y-direction,〈0,1〉

v=〈v1,v2〉—> ______

v1î + v2ĵ

When given an angle, û = ____

cosθî + sinθĵ or 〈cosθ, sinθ〉

Plane vector problems: plane vector = p, wind vector = w

True course: ____

ground speed: ____

heading (direction): _____

always measure angle from _____

p+w

|p+w|

û = p+w / |p+w|

x-axis

R2 - “the xy plane”

has origin, ____, scale, orientation

axes

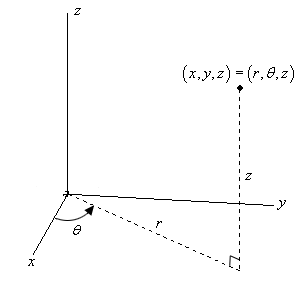
Cylindrical coords: (_______)

Relating cylindrical to cartesian

x=_____

y=_____

z=_____

Relating cartesian to cyl

r=______ *r is NOT distance from origin to point, it’s to the projection of the point on the xy plane

θ=______ *must match quadrant and octant

(r, θ, z)

rcosθ

rsinθ

z

√(x²+y²)

tan^-1 (y/x)

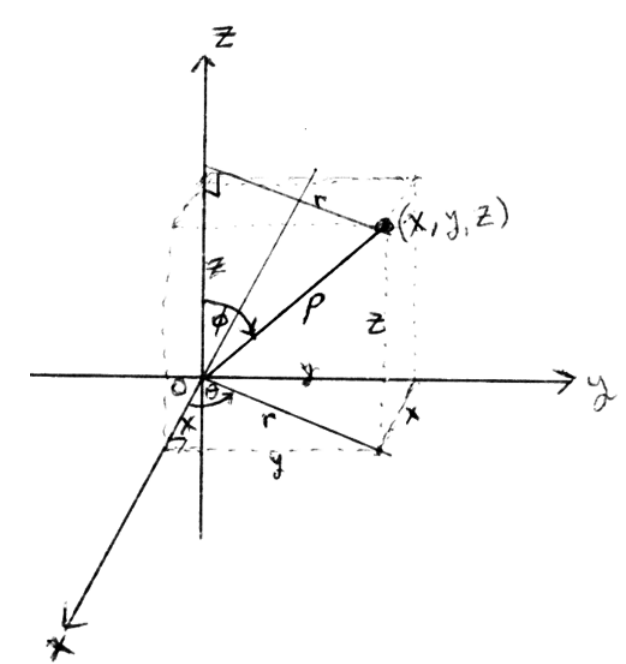
R3 spherical coords: (_____)

ρ = dist from ____ to ____. ρ ____

θ = angle from x-axis to projection of the point on the xy plane

φ = angle from _____. __≤ φ ≤__

Relating spherical to cartesian

x=

y=

z=

Relating cartesian to spherical

ρ=

θ =

φ =

Relating cyl to sph

p =

Relating sph to cyl

r=

z=

(ρ, φ, θ)

origin to point. ρ≥0

θ is just like cyl, 0 ≤ θ ≤ 2π

positive z axis. 0 ≤ φ ≤ π

ρsinφcosθ

ρsinφsinθ

ρcosφ

√(x²+y²+z²)

tan^-1 (y/x)

cos^-1 (z/ρ)

√(r²+z²)

ρsinφ

ρcosφ

Two vectors u and v are called parallel if v = ___ for some (nonzero) scalar k.

ku

vector form of a line in R3

Parametric Equations of a Line in R3

Symmetric Equations of a Line in R3

For point ____ and direction vector ______

In symmetric, if c=0, then do

(x0, y0, z0)

〈a,b,c〉

x-x0/a = y-y0/b, z=z0

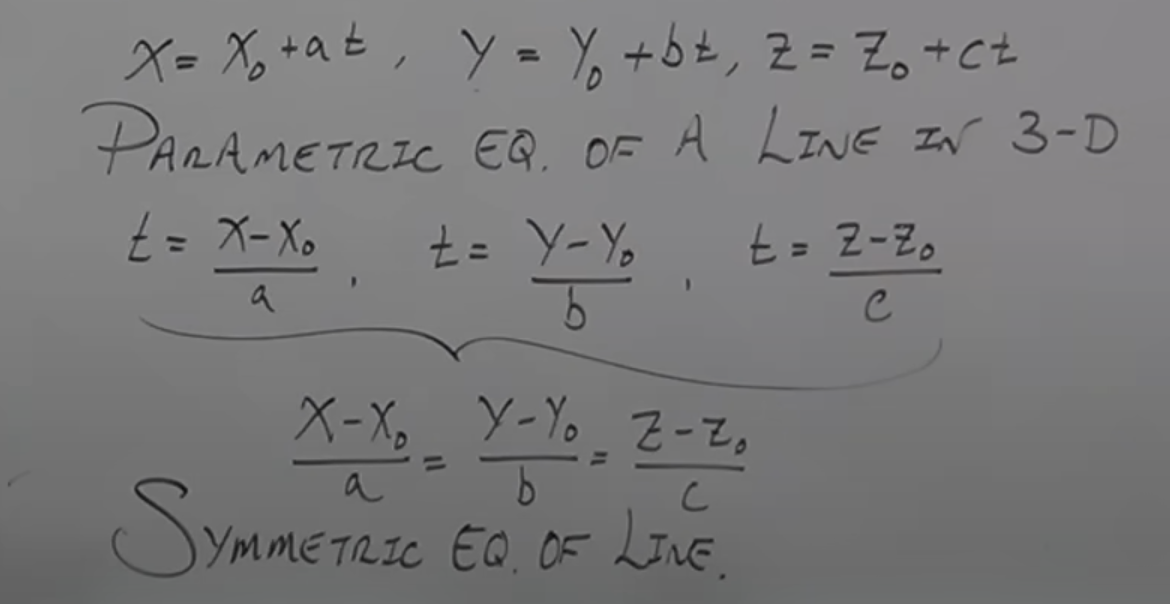
How to see if lines in R3 intersect

1. find parametric equations of both lines

2. Set the x’s, y’s, z’s equal

3. there are 3 equations in system of equations, use two to solve for t1 and t2

4. use the 3rd equation u didn’t choose before, plug in t1 and t2 and see if you get the same # on both sides

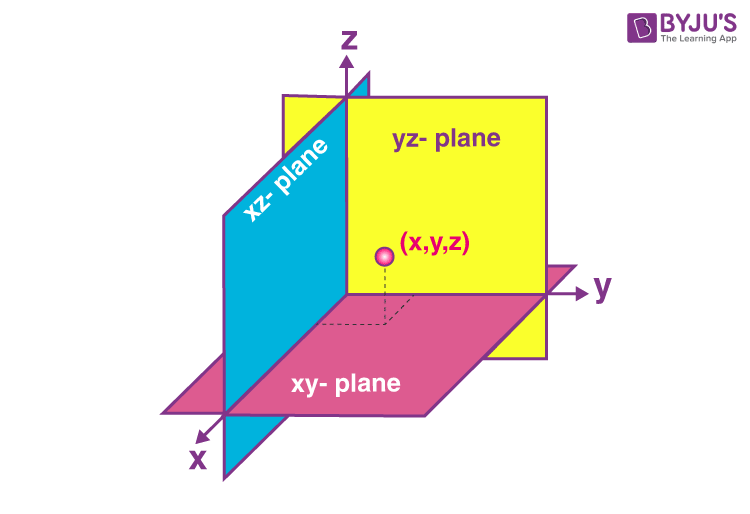
see where line crosses coordinate planes

xy plane

xz plane

yz plane

set z=0

set y=0

set x=0

solve for t and plug into parametric eqs

3D Plane

Distance formula for 3D plane between P1(x1,y1,z1) and P2(x2,y2,z2)

d=√ (x2−x1)²+(y2−y1)²+(z2−z1)²

Midpoint formula for 3d plane

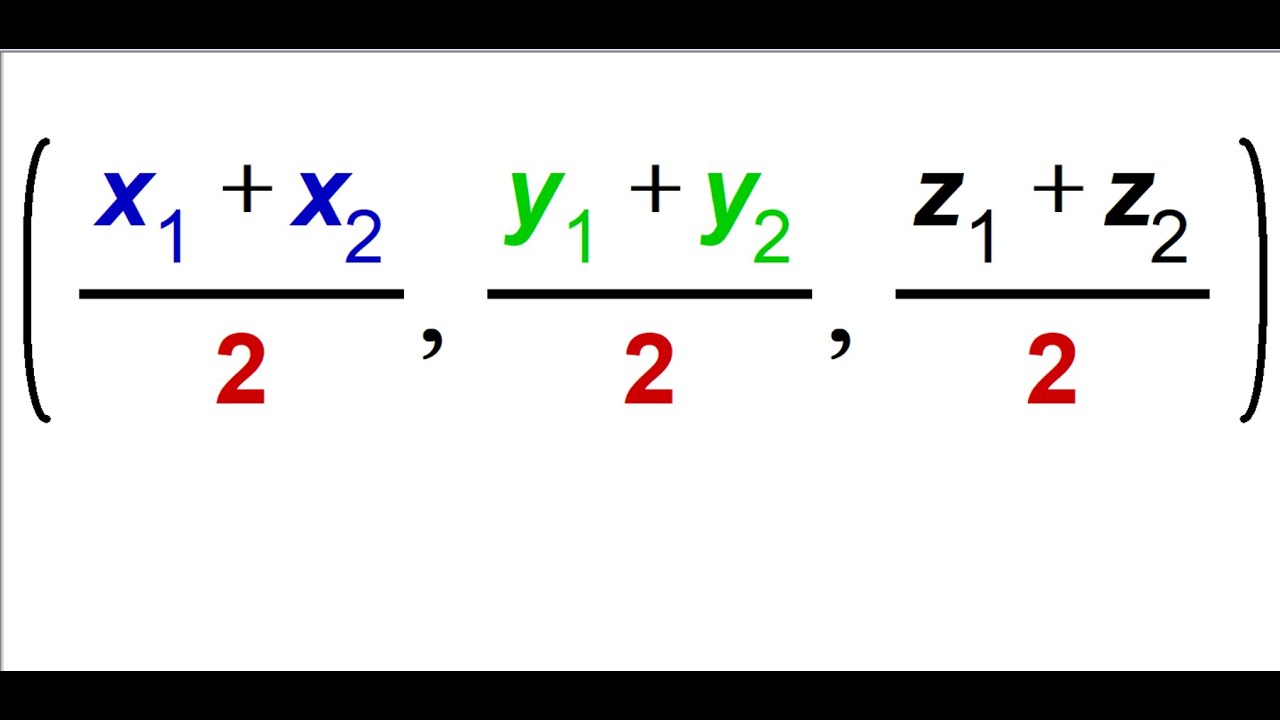
sphere equation: ____

center: _____

radius: ___

(x-h)²+(y-k)²+(z-L)²=r²

(h, k, L)

r

how to complete the square to create sphere equation

1. moving the constant to one side

2. dividing by the leading coefficient

3. adding ____ to ____ of the equation

4. factor

(b/2)², both sides

how to check if vectors are parallel:____

a || b iFF a = c*b

see if they’re scalar multiples - factoring

how to FIND parallel vectors

use unit vector

component along an axis=

ax=

ay=

az=

where α, β, and γ are angles made with the positive x-, y-, and z-axes

∣a∣⋅cos(angle with that axis)

∣a∣cosα

∣a∣cosβ

∣a∣cosγ

how to define the plane x=2 in R3 to avoid ambiguity

{(x,y,z): x=2}