Circular Motion

X

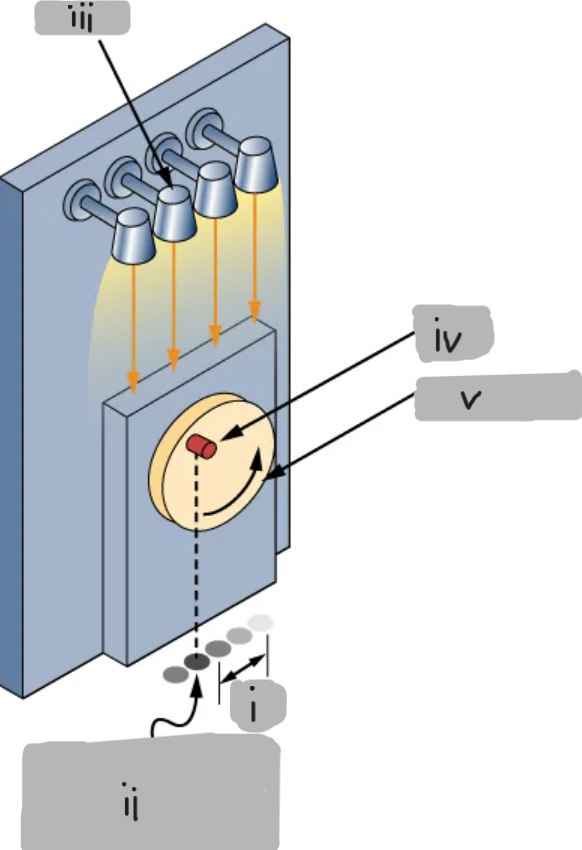
(i)

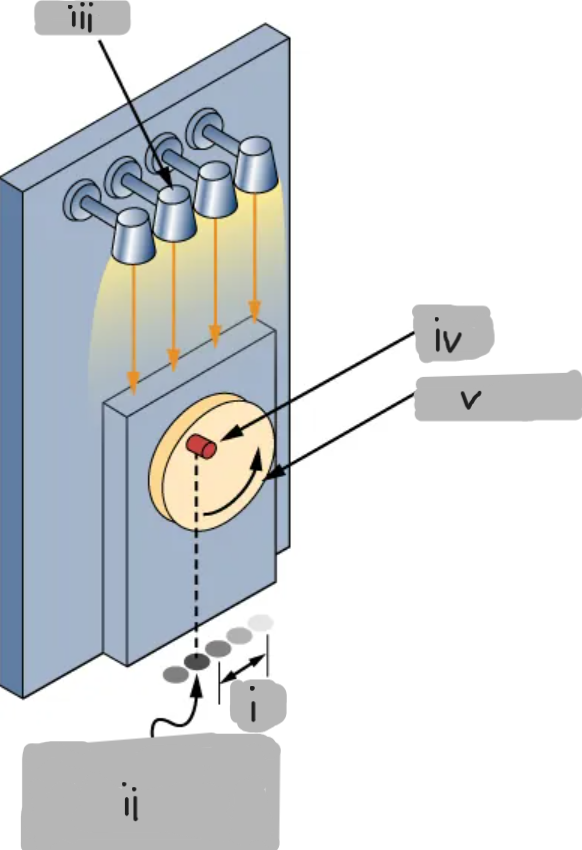
Shadow undergoes simple harmonic oscillation

(ii)

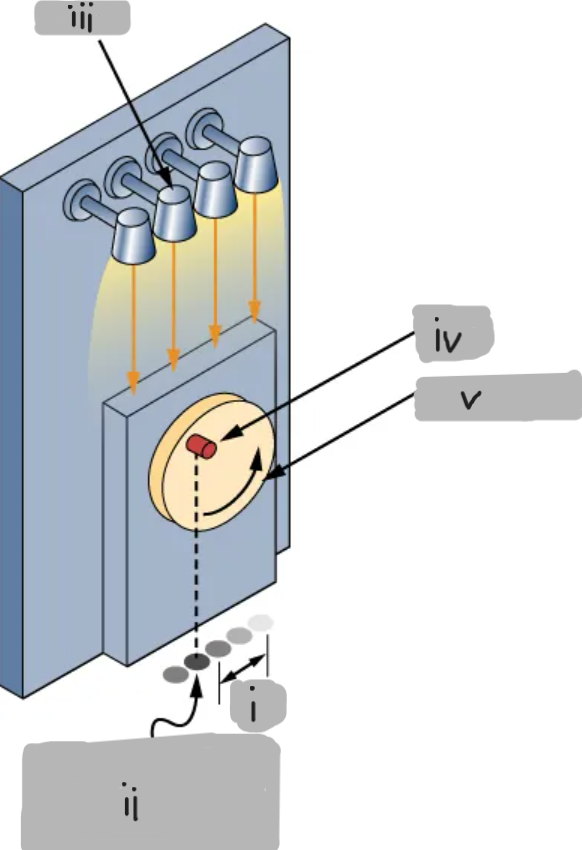
Lights

(iii)

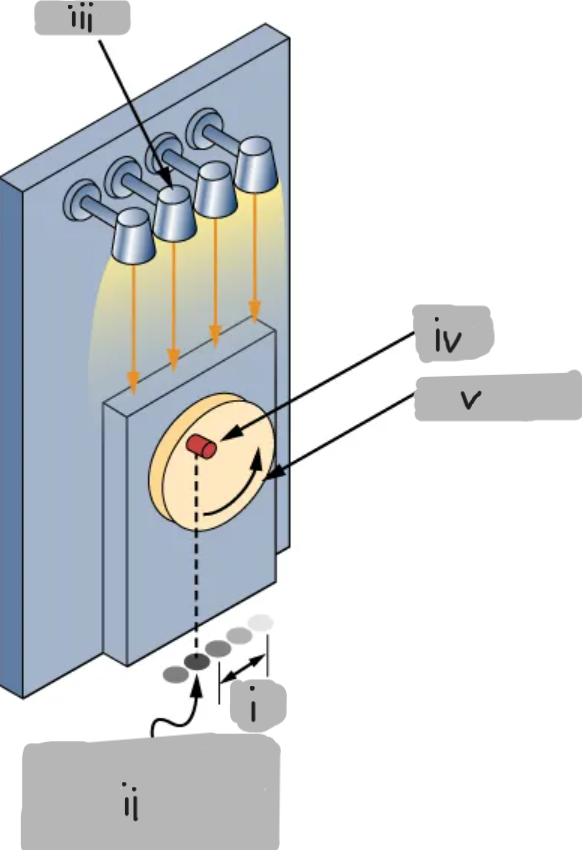
Peg

(iv)

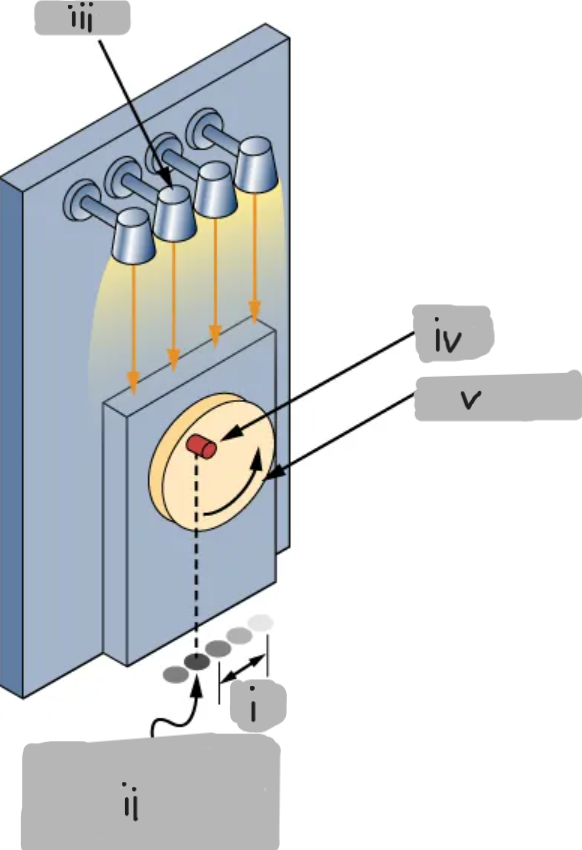
Vertical disk

(v)

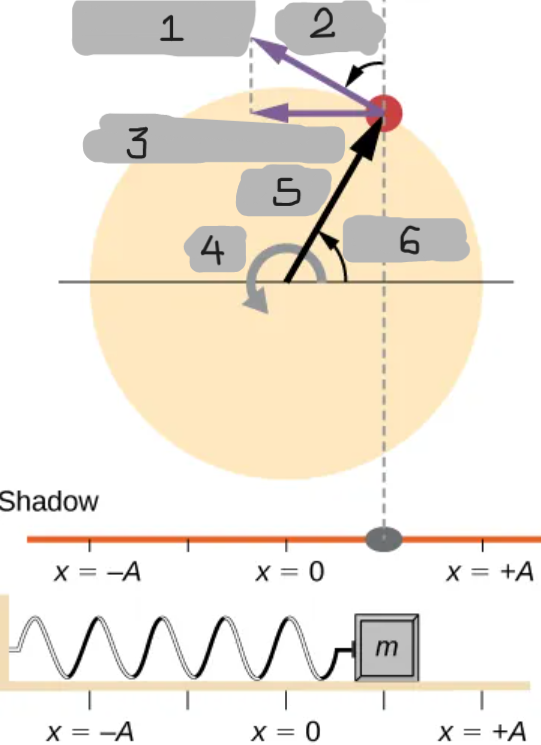
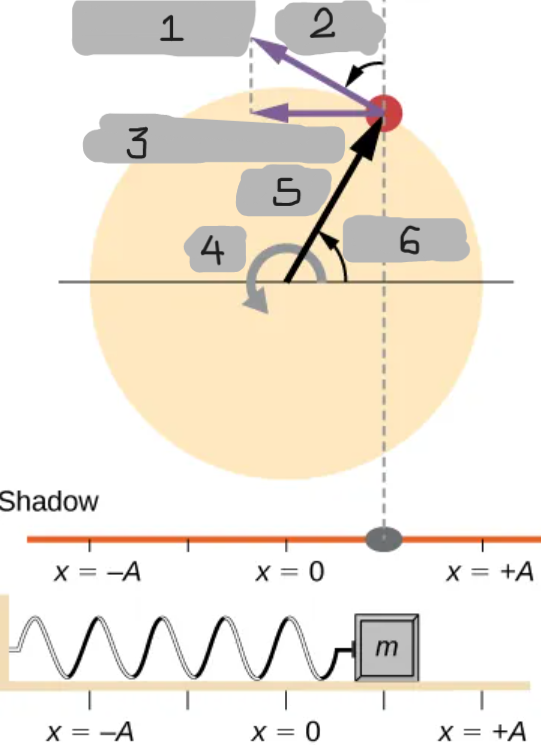
Uniform Circular Motion Model of SHM

• SHM can be modeled by projecting the motion of

• A point moving in a circle at constant angular speed onto a diameter

• The projection of this motion behaves exactly like a mass oscillating on a spring.

SHM is the projection of uniform circular motion onto a diameter. The shadow of a point moving in a circle at constant angular speed oscillates back and forth in SHM.

How is simple harmonic motion (SHM) related to uniform circular motion?

Peg-and-Shadow Demonstration

• A peg attached to a rotating disk casts a shadow

• That shadow oscillates back and forth in simple harmonic motion (SHM)

• The shadow’s position represents the oscillating mass on a spring.

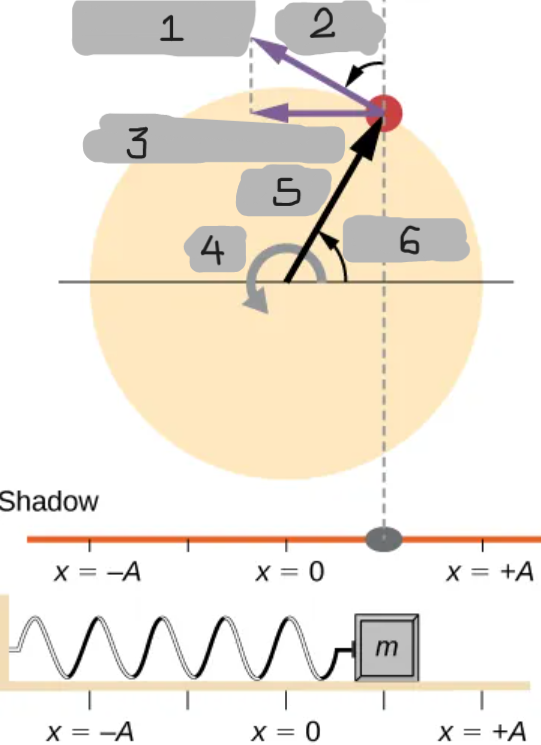
The amplitude A corresponds to the radius of the circular path. It is the maximum displacement from the equilibrium position.

What does the amplitude A represent in the circular motion model of SHM?

Angular frequency (ω)

• The constant rate of rotation of the disk, related to the oscillation frequency

• It determines how fast the shadow (or block) completes one oscillation

ω = 2πf

Mathematical representation of Angular Frequency in circular motion

x(t) = Acos(ωt)

Equation that describes the position of the shadow or oscillating block over time (gives the displacement of the shadow or the oscillator as a function of time).

tangent

In a uniform circular motion, the velocity is _______ to the circle.

It means that velocity in a uniform circular motion only changes its direction, and not its magnitude or speed.

What does it mean when someone says: “In a uniform circular motion the velocity is tangent to the circle.”

vmax = Aω

Equation for the speed at which the peg moves in a circle

horizontal

Shadow’s velocity in the Peg-and-Shadow Demonstration is a __________ component.

At x = ±A

When is the velocity of shadow is zero in the Peg-and-Shadow Demonstration

At x = 0

When does the shadow has maximum velocity in the Peg-and-Shadow Demonstration

vmax = ±Aω

Formula to calculate shadow’s maximum velocity in the Peg-and-Shadow Demonstration

v = -vmaxsin(ωt)

Equation to calculate the velocity of the shadow (or block) at any instant

turning points

In the Peg-and-Shadow Demonstration, the acceleration is maximum at the _____________.

amax = Aω^2

Formula to calculate shadow’s maximum acceleration in the Peg-and-Shadow Demonstration

a = -amaxcos(ωt)

Equation to calculate the acceleration of the shadow (or block) at any instant

At x = 0

When does the shadow has zero acceleration in the Peg-and-Shadow Demonstration

radius

The _____ of the circular path equals the amplitude A.

displacement

The x-projection of the peg’s position corresponds to _____________.

x-component

___________ of the peg’s tangential velocity equals the block’s velocity on the spring.

Velocity and acceleration are 90° out of phase; when velocity is at its maximum, acceleration is zero, and when acceleration is at its maximum, velocity is zero.

What is the relationship between velocity and acceleration in SHM?

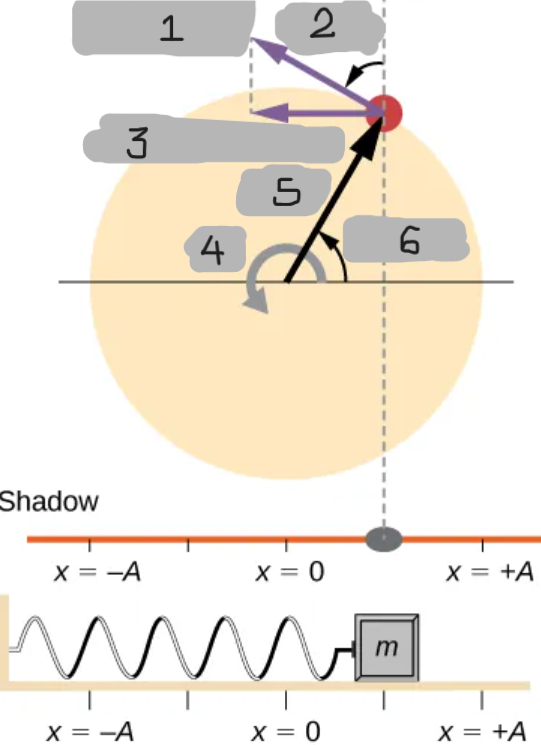
Phase Angle

• Represents the angular position of the rotating peg at time t.

• Connects circular motion to oscillatory motion.

• This value determines both velocity and displacement in Simple Harmonic Motion.

θ = ωt

Mathematical representation of the phase angle

Just as a point in circular motion has constant speed and changing direction, an oscillator in SHM has constant total energy but continuously exchanges between potential and kinetic energy as it moves.

Explain how uniform circular motion is similar to the Simple Harmonic Motion?

The disk must rotate at ω=2πf, the same angular frequency as the block’s oscillation.

What must be the disk’s angular frequency for the shadow to match the block’s motion?

|vmax| = Aω

(1)

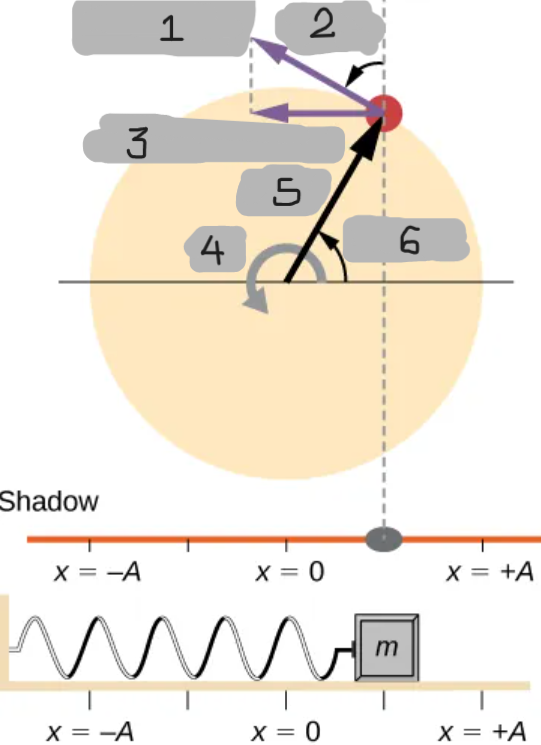
θ = ωt

(2)

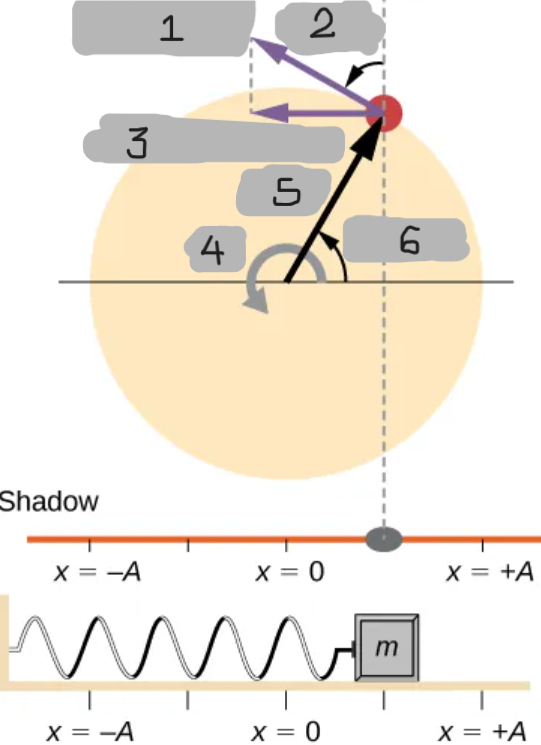
v = -vmaxsin(ωt)

(3)

ω

(4)

r = A

(5)

θ = ωt

(6)