skewness, kurtosis, and the Normal distribution

skewness

• describes the degree to which the distribution of a dataset is asymmetrical

  • (left and right side are not mirror images)

• the comparison between the mean and the median in your dataset is one means of understanding “skewness: in your data, together with loooking at teh histogram of your distribution

negative skew

data that is skewed to the LEFT

positive skew

data that is skewed to the RIGHT

positively skewed distributions: means is ____ than the median

higher

negatively skewed distributions: means is ____ than the median

lower

symetrica distributions: means is ____ to the median

equal

Alternative Pearson Mode Skewness

• calculate a statistic that describes the direction and extent of skewness

  • skew = 3*(mean-median)/standard deviation

• google sheets: =skew

interpreting the skewness results

1. if your data is skewed

   1. if your result is 0, then your data is perfectly symmetrical.

   2. if the value is between -.5 and -0.5, we can still consider the data approx. symmetrical

2. the direction of the skew

   1. skewness is greater than .5 —> positively (right) skewed data

   2. skeweness is less than -0.5 —> negatively (left) skewed data

3. how substantially your data is skewed

   1. the larger your skewness statistic, the more strongly your data is leaning to the left or right, and/or the more distortion you have from outliers

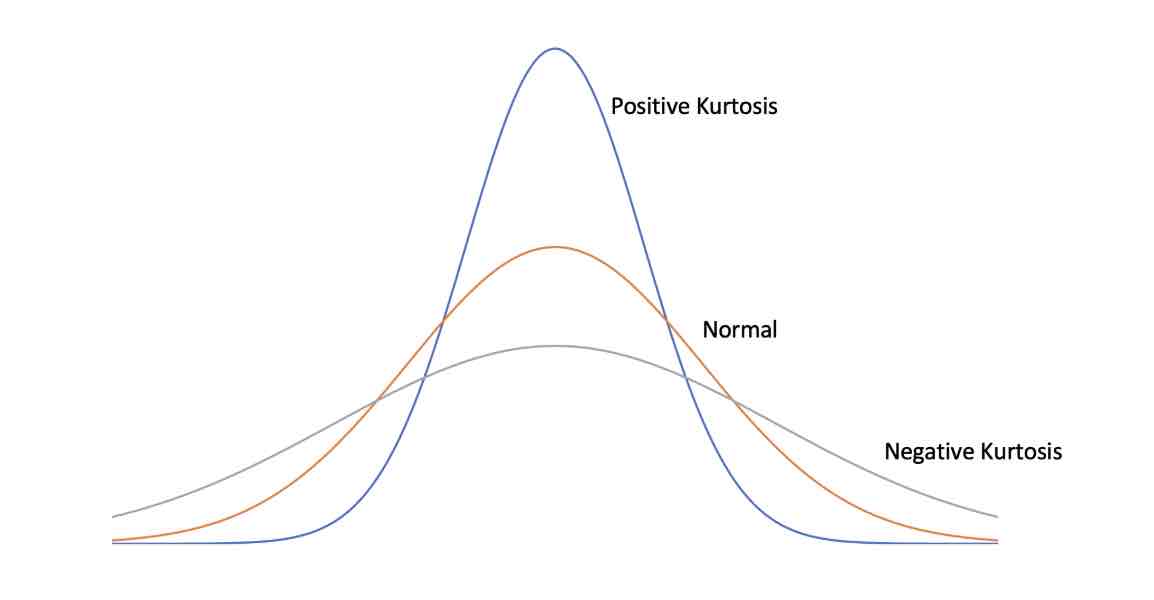
kurtosis

• statistic that describes the shape of your data distribution (like skewness)

  • the extent to which data is clustered around your mean (or peak of the distribution), or spread out more evenly towards the high and low ends (or tails) of your distribution

same skewness but different kurtosis (image)

how to calculate kurtosis in google sheets

= kurt

interpreting kustosis

• if its greater than 2 —> considered more peaked than normal (leptokurtic)

• if its less than 2 —> much flatter than mormal (platykurtic)

• between -2 and 2 —> considered close to normal (mesokurtic)

the normal distribution

• describes a data distribution where there is no skewness (and the mean and median are the same) and kurtosis is zero

examples of normal distribution (that tend to occur naturally)

• people’s heights

• test scores

• IQ

• salary

• points scored in sports

GENERAL RULE

• skewness should be between -0.5 and 0.5

• kurtosis should be between -2 and 2