Further Mech - Circular Motion - Physics

1. State the following number of degrees in radians.

• 90

• 270

• 360

• 180

• 90 = π/2

• 270 = 3π/2

• 360 = 2π

• 180 = π

2. Define angular velocity.

The angle swept out per unit time ω = θ/t.

3. Explain why ω = 2π/T is a valid equation.

• T is the time period, which is the time taken for one complete cycle/ circle to be completed.

• The angle in radians that would be swept out for 1 complete circle is 2π radians.

4. Derive the expression v = rω

• v is the tangential/orbital velocity

• v = ∆s/∆t

• ∆s is the arc length, which according to the definition of the radian is equal to ∆s = rθ.

• So v = ∆s/∆t = rθ/t = rω.

5. Derive the expression for acceleration in circular motion.

SEE photo

6. Explain why an object moving in a circle requires a centripetal force.

• When an object moves in a circle, its velocity changes direction.

• This is an acceleration.

• Due to N2L, the object must experience a resultant force towards the centre of the circle.

7. Define centripetal force.

The resultant force acting on an object towards the centre of a circle for an object in circular motion.

8. State the two equations for centripetal force.

• F = mv²/r = mrω².

9. By considering the forces and resultant foce acting in circular motion, explain how the size of the normal contanct reaction force varies as an object travels from the bottom of the London Eye to the top.

• The resultant force at each point must always act towards the centre as the obejct moves in a circle.

• So at the top, the resultant force is downwards: F_resultant = F_centripetal = mv²/r = W-R.

• And at the bottom, the resultant force is upwards: F_resultant = F_centripetal = mv²/r = R-W.

• Given that the speed v, mass m and radius r of the circle do not change in one rotation, the resultant centripetal force must be constant. This means that at the top, the reaction must be less than the (constant) weight R<W, and at the bottom, the reaction must be more than weight R>W.

10. A ball of mass m, whcih is fixed to the end of a light string of length l, is released from rest at X. It swings in a circular path, passing through the lowest point Y at speed v. If the tension in teh string at Y is Tm what is the equation representing a correct application of Newton’s laws of motion to the ball at Y.

• The resultant force = centripetal force = mv²/l

• at Y, the resultant centripetal force must be upwards (towards the centre of the circle).

• The force arrow diagram: (T_upwards > W_downwards)

• Taking upwards forces as positive: mv²/l = T - mg (answer C)

11. A car, mass m, drives over a circular hump-back bridge of radius r, with a constant speed v. When it is at the top of the bridge, the force on the car from the bridge is given by:

• Resultant force = centripetal force = mv²/r.

• The resultant force must be downwards because that is the direction of the centre when the car is at the top.

• Force arrow diagram at top: W_downwards > R_upwards because resultant force must be downwards.

• So the force on the car from bridge = R = W - mv²/r

• (Answer is D).

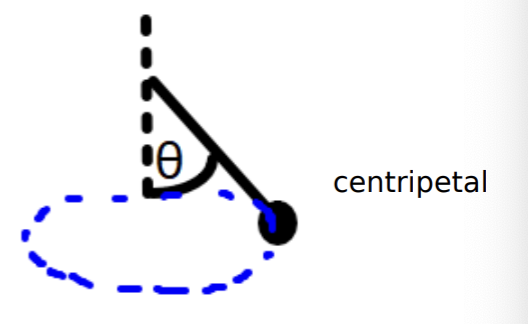
12. Identify the force that provides the force in thsi example. A ball is spun around a string in a circle.

Resultnat force towards the centre of the circule = horizontal component of tension = Tsinθ.

13. The Moon orbits the Earth. Which of the following diagrams correctly represents the force(s) acting on the Moon.

• The answer is A. The centripetal force is not an additional force. It is the resultant force towards the centre of the circle that acts on objects in circular motion. So the centripetal force in this case is provided by the gravitaional force, which is the only force that acts on the moon.

14. When standing on weighting scales, the reading shown is the reading of the reaction force, not weight. A person standing on the north pole reads 500N when they stand on weighing scales. Calculate the reading they would see at the equator. Radius of earth = 6400km.

• At the North Pole, the person is stationary, so W = R. This means W = 500N. m = 500/9.81 = 50.97kg.

• At the equator, the person is moving in a circle, where the centre of the circle is the centre of the earth.

• Force arrow diagram at the equator, where the person is travelling in circular motion: (W_downwards > R_upwards).

• Resultant force = centripetal force = mv²/r = W-R

• Given that we do not know their speed, v, we should use the otehr equation for centripetal force: F = mrω², so we can use the fact that the time period of the Earth is 24 hours.

• As ω = 2π?T = 2π/ (24×60×60) = 7.27 × 10^-5 rad s^-1

• mv²/r = mrω² = W-R

• R = W - mrω²

• R = 500 - 50.97 × 6400 × 10³ x (2.72 × 10^-5) = 498.3N

• So the person appears very slightly lighter at the equator than the north pole.