Atomic and Molecular orbitals

Atomic orbital

Region of space that is occupied by an electron in an atom

Tells us about x, y and z coordinates of the electron

𝚿 = AOs

Quantum theory

Allows us to calculate atomic orbitals

Schrodinger equation which gives wavefunctions 𝚿

𝚿²

Tells us probability of finding the electron

Electron density plots

Also known as probability density representations of electrons

Describe the electron as located within a specific region of space (the atomic orbital) with a particular electron density at each point in space

Dot density representations

Cloud of dots

Density of dots in any particular region is a pictorial representation of the electron density in that region

Dots ∝ electron density

Dots = electron density

Dots = 𝚿² at particular point in space

Nucleus at centre

Dense dots = high e- density

Microscope slide through the nucleus and each time an electron crosses the nucleus, a dot is formed on the slide

Ground state

Lowest energy state of the electron in the atom

Boundary surface representations

Simple single line plot that denotes the shape of the orbital

Encloses approx. 95-97% of the probability of finding an electron

Easy to draw

Shows less detail than dot density plots

Can be shaded or unshaded

Boundary surface and dot density of s-orbitals

Spherical symmetrical

Nucleus is at centre of sphere

No nodal planes in the surface boundary

The more nodes, the higher the energy

1s - orbitals getting bigger → 0 nodes

2s - orbital energy increasing → 1 node

3s - increase in radial node → 2 nodes

Nodal plane

Is a plane where the probability of finding an electron is zero

Boundary surface and dot density of p-orbitals

3p orbitals of a shell are identical but axes lie along x, y, z

px, py, pz are used instead of ml, quantum number labels

Nucleus at (0,0,0)

Nodal plane runs through the nucleus

Different coloured lobes = different amplitudes of 𝚿

3p and 2p look similar but 3p is much bigger and has nodal surface

Boundary surfaces and dot density of d orbitals

Nucleus at (0,0,0)

Ones that lie on axes are ones with squared in name - dz² and dx²-y²

dz² combination of dz²-dx² and dz²-dy²

2 nodal planes runs that intersect at the nucleus except dz²

Different coloured lobes = different amplitudes of 𝚿

Wavefunction

All orbitals have form 𝚿 = R(r).A(θ,𝚿)

Radial wavefunction

R(r)

Describes how wavefunction varies with distance from nucleus - size

The spherical harmonic

A(θ,𝚿)

Describes how wavefunction varies with angle around the nucleus - shape

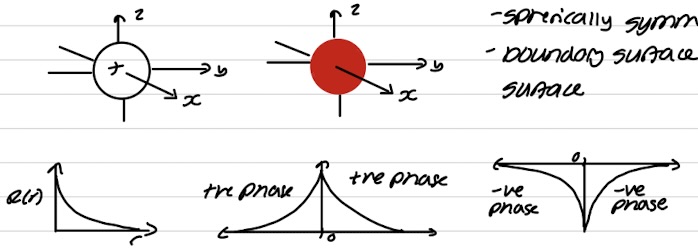
Radial graph info

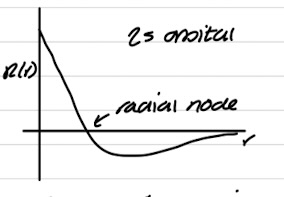
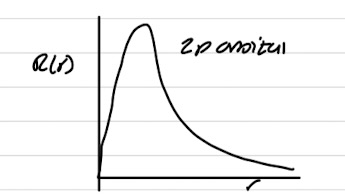
Radial wavefunctions pass through 0 = radial node

s-orbital has a non-zero amplitude at nucleus

all other orbitals are 0 (vanish) at nucleus

All orbitals go to 0 at large distances from nucleus - big r

Radial graph of 1s orbital

Radial graph of 2s orbital

Radial wavefunctions pass through 0 = radial node

Radial graph of 2p orbital

Orbital shading and phases

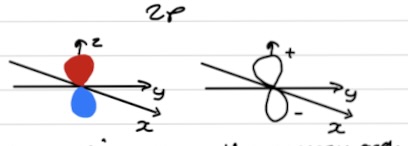
Different colours = different phases or signs

Shading relates to the sign of the wavefunction

+/- doesn’t relate to charge

Important for bond formation

Phase

Property of waves/wavefunctions and the general behaviour of electrons are waves

Tells you whether amplitude (height) of the wave is +/-

+ve amplitude = +ve phase

-ve amplitude = -ve phase

Phase and nodal properties for s orbital

Spherically symmetrical

Boundary surface has a constant phase across its surface

Phase and nodal properties for p orbital

One phase for each lobe - different for each

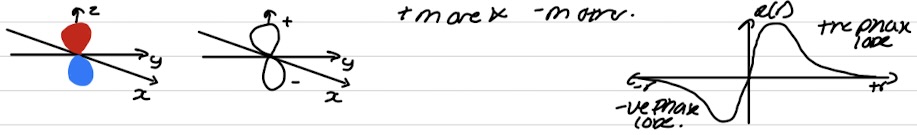
Orbital energies in H atom

Energies come from solving Schrodinger equation

Quantum numbers

Define specific properties of the orbitals

n, l, ml

Each orbital is defined by a set of 3 quantum numbers

All orbitals with the same n belong to the same shell

All orbitals of the same shell that have the same value of l belong in the same sub-shell

Individual orbitals are identified by their value of ml

Maximum number of 2e- that can be accommodated in each AO

Rules govern the existence/number of subshell

Principle quantum number, n

Corresponds to the orbital energy level or shell

Orbitals of a shell have the same energy and approx the same radius

n is an integer with values 1 to ∞

Angular momentum quantum number, l

Orbitals of each shell are divided into sub-shells, labelled l

l determines the shape

For any principle quantum number, n l=0, 1, …, n-1

l=0 → s-orbital

l=1 → p-orbital

l=2 → d-orbital

l=3 → f-orbital

Magnetic quantum number, ml

A subshell with quantum number, l consists of 2l +1 individual orbitals

ml relates to the orientations of different orbitals

For a given value of l, ml takes the value l, l-1, l-2, 0 ,…, -1

Molecular orbital (MO) theory

Wavefunctions are built up to describe the regions of space that the electrons occupy in the molecule

Electrons can be delocalised across the molecule rather than localised in 2-centre bonds

Molecular orbitals can be constructed from atomic orbitals for simple molecules

Hydrogen, H2

Experimental facts

• exists as H2 molecule

• bond length = 74pm

• BDE = 458kJmol-1

Chemistry

• Colourless, odourless

• highly combustible → greener combustion engines and boilers

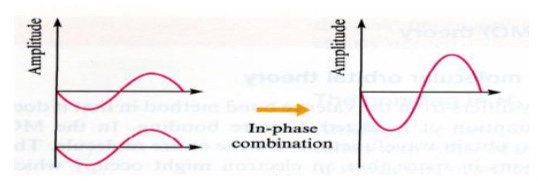
Constructive interference

Size of wave increases

Amplitude increases

In plane combination

Add waves up

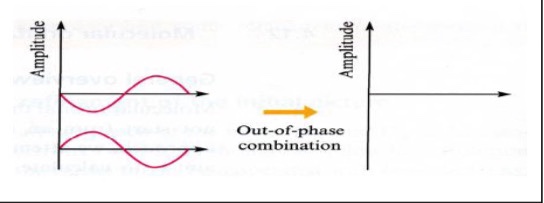
Destructive interference

Size of waves decreases

Amplitude decreases

Subtract waves

Out of plane combination

𝚿 = 0 so 𝚿² = 0 → probability is zero everywhere

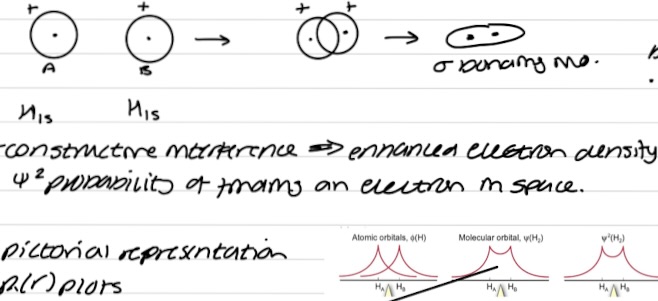
Bond formation in same phase

Build up of e- density between the nuclei

Constructive interference → enhanced electron density → turns on interaction between 2AOs

𝚿² probability of finding electron in space - extra probability between the nuclei → lower energy compared to 2 separate AOs

𝚿MO = ØA + ØB

𝚿² = (ØA + ØB)² = زA + زB + 2ØAØB → shows addition of e- density between nuclei

Bond formation in different phases

Forms a nodal plane - plane where there is zero probability of finding electrons → σ* antibonding MO

Destructive interference → interaction is turned on

𝚿² - reduced probability of finding electrons between nuclei → higher energy than 2 single AOs

𝚿MO = ØA - ØB

𝚿² = (ØA - ØB)² = زA + زB - 2ØAØB → shows reduction of e- density between nuclei

Bonding MOs

Lower in energy than 2 separate AOs → stable

Formed by in phase combination of AOs

Build up of electron density between nuclei

Stabilises E compared to AOs

Antibonding MOs

Higher in energy than 2 separate AOs → destabilised

Formed by out of phase combination of AOs

Reduction of e- density between nuclei of 2 atoms - nodal plane

Destabilises E compared to AOs

Molecular orbital diagram general rules

E increases at LHS

Show where the e- go in a molecule - dotted line

AOs on the outside

MOs in the middle

number of AOs = number of MOs

Aufball principle

Building up principle

Fill up e- in the lowest MO first

Pauli principle

2e- maximum in each MO orbital

e- must have opposite spins - ms = quantum number = ± ½

Hund’s rule

If degenerate orbitals are available, electrons will occupy them individually before pairing up

Spins will be parallel

Bond order

½(number of e- in bonding MOs - number of e- in antibonding/non-bonding MOs)

Energies of AOs

Numbers on horizontal lines are the number of e- in that AO

Use for mixed molecules

Bigger AOs have poorer overlap than smaller AOs → bigger AOs have weaker bond than smaller AOs

Energies trends across row

E of 2s and 2p orbitals goes down

Gap between 2s and 2p increases

Energy of 1s goes down very sharply after He

Obtain plot of E levels

Doing quantum chemical calculations

Experiments - photoelectron spectroscopy, photoionisation

Do core orbitals matter

No

Usually leave out core orbitals

Using just the valence AOs, use just valence electrons

Valence orbitals

Outer shell - must be considered for MO formation

Biggest n shell

Core orbital

Inner shell - can be ignored for MO formation

Any shells smaller than n

MO interactions for valence orbitals

Only significant for valence orbitals

Overlap of core orbitals cancel out

Overlap of core orbitals is small - weak bonding/antibonding interactions → very small bonding effect

p orbitals

py - out of the page

pz lies along internuclear bond

l = 1

ml = +1, 0, -1 → orientations

In phase combination of pz orbitals

Spherically symmetrical

Constructive interference

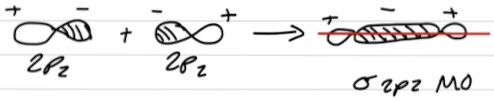
Out of phase combination of pz orbitals

Destructive interference

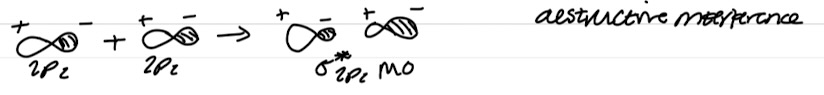
In phase combination of px orbitals

Constructive interference

Forms nodal planes

Same as py AOs just rotated 90°

π2px and π2py = same E

Out of phase combination of px orbitals

Destructive interference

σ bonds are cylindrically symmetrical along internuclear axis

π bonds have a nodal plane along internuclear axis

No net interaction between pz and px/py

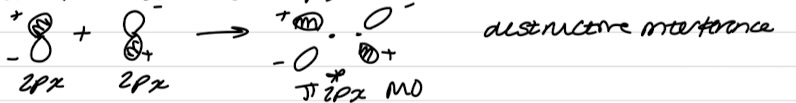
Interaction between pz and px/py

No net interaction

Wrong shape/symmetry to overlap

Positive lobes have same wavelength so bonding interaction

Positive and negative lobes have opposite wavefunctions so antibonding interaction

No net interactions as bonding and antibonding interactions cancel out

Energy ordering of MO formed by p-orbital overlap

6AOs → 6MOs

Most bonding AO (σ2pz) will always correspond with the most antibonding MO (σ*2pz)

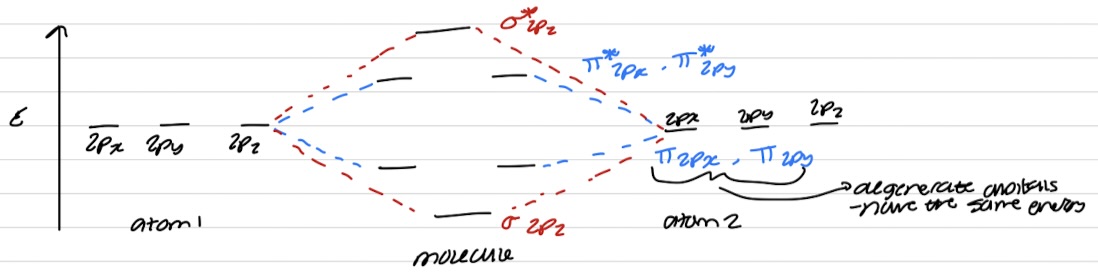
MO labels

+ → + = (g)

- → - = (g)

+ → - = (u)

- → + = (u)

g = same phase

u = different phase

Only certain AOs overlap to form MOs

Only AOs with the same symmetry with respect to the internuclear axis can overlap to form MOs

An s orbital is cylindrically symmetric about internuclear axis so is pz orbital → overlap

px/py orbital is not cylindrically symmetric about internuclear axis → no overlap and energy requirement need

Homo-nuclear diatomics

Same size orbitals

Heteronuclear diatomics

One orbital is bigger than the other

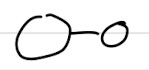
Similarities between diatomics

Only orbitals of the same symmetry can overlap to form bonds

Pairs of orbitals will only have significant overlap if they are relatively close in energy

Differences between diatomics

Different types of orbitals and sizes on the two sides of the molecule

AOs are different Es, each bonding and antibonding MO is unequally shared between 2 atoms → MOs skewed

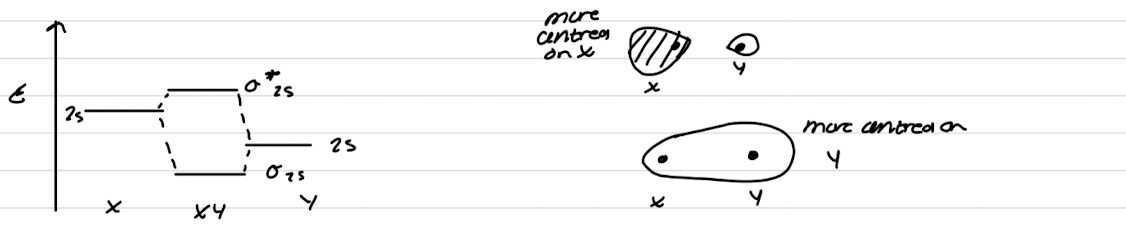
MO formation in a heteronuclear diatomic XY

ZeffY>ZeffX → Y is more electronegative = higher Z

𝚿σ2s = Cx𝚿x + Cy𝚿y Cy>Cx → tells us about % of the AO in the MO

𝚿σ2s = Cx’𝚿x + Cy’𝚿y Cx’>Cy’ → tells us about % of the AO in the MO

If E2sX- E2sY → Cx ≃ Cy → 50:50 contribution of 2 AOs

Drawing MO diagram for heteronuclear diatomic

1. List occupied AOs for both atoms - ignore core and keep valence

2. Identify atom with greatest Zeff. AOs for this atom will lie lower in energy

3. identify the AOs that overlap

   • Close in energy

   • Appropriate symmetry

     4. Sketch MO and put in electrons

Non-bonding electrons

Same E as one of the AOs on an atom in the molecule

It is an MO

Can be occupied with electrons

Neither stabilises or destabilises a molecule compared to the atoms that form it

Electron do not contribute to BO

No effect on E

Photoelectron Spectroscopy

Energy of orbitals

Identity of orbitals

Checks MO theory is correct

hv = BEe-mMO + KEe-

KEe- = kinetic energy and is measured experimentally

BEe-mMO = binding energy and is equal to the E of the MO

Orbital mixing

AOs of the same symmetry and energy mix to form MOs

MOs of the same symmetry and close in energy can mix

When 2 orbitals mix, one of the orbitals increases in energy (antibonding) and the other decreases in energy (bonding)

Some molecules show σ/π crossover → the size of the energy gap between the orbitals between the orbitals overlapping

Can be called σ/π crossover or sp mixing

O2 & F2 have typical ordering of MOs → σpz below πpx,py

B2 → N2 have inverted ordering of MOs → πpx,py below σpz

Bond enthalpy and bond order

Bond enthalpy increases as bond order increases

Bond distance and bond order

Bond distance decreases so bond order increases

Bond enthalpy and bond distance

Bond enthalpy decreases as bond distance decreases

Bond stretching frequency and bond order

Bond stretching frequency increases as bond order increases

Paramagnetic

Drawn into magnetic field

Molecule has unpaired electrons

Diamagnetic

Pushed out of magnetic field

Molecule has all electrons paired up

MO diagrams tell us

Why some molecules exist and other don’t

How strong bonds are

Whether a molecule is paramagnetic or diamagnetic

What electronic transitions take place

Isoelectronic species

If 2 species have the same number of electrons

Often displat similar properties but there can be differences

Interaction of σ2s and σ2pz orbitals

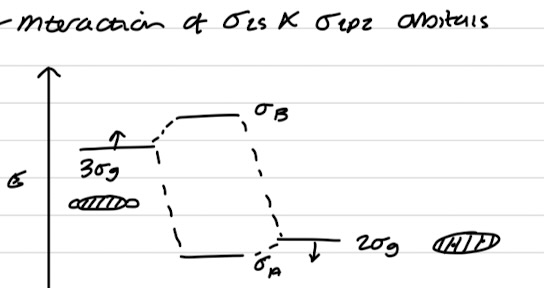
Interaction of σ*2s and σ*2pz orbitals

MOs of polyatomic orbitals

Combine the AOs that have the right symmetry and energy

MOs can extend across the entire framework of a molecule - not limited to region between 2 orbitals

Electrons are delocalised across the whole molecule

MO of polyatomics give us insight into

The geometric sequence of a polyatomic orbital

How the stability of a polyatomic molecule changes if it is oxidised, reduced or interacts with a proton

The way in which the molecule binds and/or reacts with another molecule → HOMO-LUMO theory

Highest occupied molecular orbital

HOMO

Lowest unoccupied molecular orbital

LUMO

Principles of MOs

1. σ bonds have lower energy than π bonds

2. The higher the number of nodes, the greater the energy

   Degenerate pair of MOs → same energy MOs

   π* node between central C atom

   σ buildup of electron density between nuclei

   π region of electronegativity is above and below nuclei

   σ* +,-,+,- alternating regions