Graph Theory Definitions:

Define - Bipartite Graph:

A graph whose set of vertices can be split into two distinct groups in such a way that each edge of the graph joins a vertex in the first group to a vertex in the second.

Define - Complete Graph:

A simple graph in which every vertex is joined to every other vertex by an edge. The complete graph with n vertices is denoted Kn.

A complete bipartite graph is a bipartite graph where every vertex of the first set is connected to every vertex of the second set.

Define - Connected Graph:

A graph is connected if there is a path between each pair of vertices.

A bridge is an edge in a connected that if removed leaves a graph disconnected.

Define - Cycle:

A closed path which begins & ends at the same vertex with no repeated edges or vetices except the first.

Define - Degree of a Vertex (Graph):

In a graph the degree of a vertex is the number of edges that enter or exit from the vertex, thus loops are counted twice.

Define - Directed Graph:

A directed graph is a diagram comprising points, called vertices, joined by directed lines called arcs - directed graphs are commonly called digraphs.

Euler’s Formula:

For a connected planar graph, Euler’s rule states that v + f - e = 2, where v is the number vertices, e is the number of edges & f is the number of faces.

Define - Eulerian Graph

A connected graph is Eularian if it has a closed trail (starts & ends at the same vertex), that is includes every edge & once only; such a trail is called an Eularian trail.

An Eularian trail may include repeated vertices.

A connected graph is semi-Eularian if there is an open trail that includes every edge once only.

Define - Loop:

A loop is an edge in a graph that joins a vertex in a graph to itself

Define - Multiple Edge:

A multiple edge is where two or more edges connect the same vertices.

Define - Hamiltonian Graph:

A connected graph is Hamiltonian if it contains a closed path (starts & ends at the same vertex), that includes every vertex (except the first one) once only.

No edge is repeated.

Define - Semi-Hamiltonian Graph:

Contains a path that includes every vertex in a graph once only but is not a cycle.

Define - Length of a Walk

The number of edges it includes

Define - Open Path

A path that starts & finishes at different vertices is said to be open.

Define - Open Walk

A walk that starts & finishes at different vertices is said to be an open walk.

Define - Path

A path in a graph is a walk in which all edges & vertices are different.

Define - Closed Path

A path that starts & finishes at the same vertex - a cycle is a closed path.

Define - Planar Graph:

A planar graph is a graph that can be drawn in the plane so that no two edges cross.

Define - Semi-Eulerian Graph

A connected graph is semi-Eulerian if there is an open trail that includes every edge once only

Define - Simple Graph:

A graph that has no loops or multiple edges

Define - Subgraph

When the vertices & edges of a graph are also vertices & edges of another graph is said to be a subgraph of graph G.

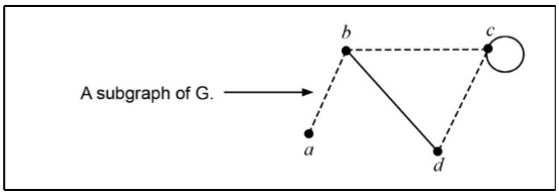
Define - Trail:

A trail is a walk in which no edge is repeated

Define - Walk:

A sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence.

A walk can include repeated vertices or repeated edges

Define - Weighted Graph:

A graph in which each edge is labelled with a number used to represent some quantity associated with that edge

Define - Connected Planar

A graph that can be drawn in the plane so that edges only intersect at vertices where evert vertex is connected by an edge.

Define Traversable Network

Exactly two odd vertices or no odd vertices

Define Bridge

An edge that connects two graphs, without this edge the two graphs are not connected to each other 

From an Adjacency Matrix how do you know if a Graph is Non-Directed:

Symmetrical across the leading diagonal

No loops - leading diagonal all zeroes

Sum of a row = degree of corresponding vertex for that row (+1 if there is a loop)

No multiple edges, all values in matrix are 0 or 1

From an Adjacency Matrix how do you know if a Graph is Directed

Not symmetrical across the leading diagonal

Sum of a row = out degree of the corresponding vertex

Sum of a column = in degree of the corresponding vertex

Define - Digraph

A graph with edges that are directed

Define - Eulerian Circuit

Covers every edge exactly once

starts & ends at the same vertex

All vertices are even

Define - Eulerian Trail

Covers each edge exactly once

Starts & ends at different vertices

Exactly two odd vertices

Define - Hamiltonian Cycle

Includes each vertex only once

Starts & finishes at the same vertex

Define - Hamiltonian Path

Includes every vertex exactly once

Starts & ends at different vertices

Define - Multiple Edge

Two or more edges connecting a pair or vertices