Linear Regression - Practice Questions (1&2 EMF)

What does β₁ mean in

y = β₀ + β₁x + u

Change in y for a 1-unit change in x, ceteris paribus

What does β₁ mean in

wage = β₀ + β₁mast + u?

(mast is a dummy variable, where 1= have master, 0=no master)

Average wage difference between those with and without master’s degree

If wage = 1500 + 500mast, what is wage with master? Any issue?

• Predicted wage = 2000

• Issue: may omit factors correlated with mast → bias risk

What is a dummy variable in regression?

• Variable coded 0 or 1 to indicate membership in a category

• Example: mast = 1 if a person has a master’s degree, 0 otherwise

Does unbiasedness require high R²?

No. Unbiasedness relies on assumptions, not on fit

R² measures fit (Proportion of variation in y explained by the model)

How to read coefficients when the dependent variable is ln(y)?

• Continuous x: +1 in x → ≈ 100·β% change in y

• Dummy D (0/1): D=1 vs 0 → ≈ 100·δ% difference in y

• Quick feel: β = 0.05 ⇒ ≈ 5% (exact 5.13%)

What is the base group in a regression with dummies?

The group where all dummy variables = 0

• Example: wage = β₀ + β₁IQ + β₂south + β₃(IQ×south), the base group is non-southerners (south=0)

What does a p-value measure in regression output?

• Probability of seeing an estimate as extreme as β^​ if the true β = 0

• Small p (<0.05): strong evidence against H₀ → effect significant

• Large p: no strong evidence → cannot reject H₀ → not significant

• p-value does not measure size or importance of effect, only evidence against H₀

What is the formula for the t-test on a regression coefficient?

Usually test H₀: βⱼ = 0, so denominator is the standard error of βⱼ

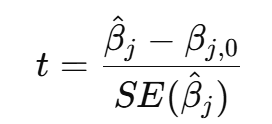
How do you test whether a group of regressors has no effect?

• Use the F-test

• Null hypothesis: all coefficients in the group = 0

• If F is large and p-value is small, reject the null

Why does multivariate regression provide a better ceteris paribus interpretation than univariate regression?

• In univariate models, β₁ may capture both x’s effect and effects of omitted correlated variables

• In multivariate models, including controls separates effects, so β₁ reflects only the effect of x

What is the population regression model in simple linear regression?

• y = β₀ + β₁x + u

• β₀ = intercept, β₁ = slope, u = error term

Interpret β₁ in:

wage = β₀ + β₁Female + u

while: β₁ = –5 and female is dummy (1=female, 0=male)

β₁ = –5 → women earn 5 less on average than men, cetris paribus

What happens if you rescale dependent variable (income € → thousands €)?

• Coefficients and SE shrink by factor 1000

• t-statistics unchanged

Two algebraic properties of OLS residuals

• Residuals sum to 0: Σû=0

• Residuals uncorrelated with regressors: Σx·û=0

Population Regression Function (PRFs) for

y = β₀ + β₁D + u

• D=0: E[y|D=0]=β₀

• D=1: E[y|D=1]=β₀+β₁

Interpret R²=0.25 in exam scores vs hours studied

25% of variation in scores explained by hours studied

Interpret β₁ in y = β₀ + β₁ln(x) + u

• β₁/100 = change in y for 1% ↑ in x

• Example: β₁=2 → 1% ↑ in x raises y by 0.02

State variance decomposition

TSS = ESS + RSS (total = explained + residual variation)

fe = β₀ + β₁Tech + u

β̂₁=0.025

se=0.010

=> Interpret & test

• Tech firms’ forecast error 2.5% higher

• t=2.5 → significant at 5%

R²=0.02. Interpret & relevance

• Only 2% of y variation explained

• Still fine for causal inference if regressors exogenous

Why log(y) can reduce heteroskedasticity?

• Compresses scale of y

• Stabilizes variance of errors

Compare log vs level wage regressions

• log(wage)=β₀+β₁Education+u → β₁ ≈ % effect of education

• wage=β₀+β₁Education+u → β₁ = absolute wage change per education year

Reading regression output

• Variable significant if p<α (1%,5%,10%)

• Significant coefficient → effect different from 0

• Non-significant → cannot reject H₀

Why high R² may be useless

Spurious regression: x and y both trend but no causality

What is an exogenous variable?

• A regressor uncorrelated with the error term (E[u|x]=0)

• Ensures OLS is unbiased and consistent

• Example: randomized treatment in an experiment

What is an endogenous variable?

• A regressor correlated with the error term (E[u|x]≠0)

• Causes OVB and biased OLS estimates

• Sources: omitted variables, simultaneity, measurement error

Why can a high R² be useless?

• R² only measures % of y’s variation explained by x

• It does not prove unbiasedness or causality

• Example: time-series data where GDP and global temperature both trend upward → regression shows high R² but relationship is spurious (driven by common trend, not causal link)

Give two endogeneity threats.

• Omitted variable (e.g. ability with education)

• Simultaneity (e.g. price & demand)

What are omitted variables?

• Relevant factors affecting y but excluded from regression

• If correlated with regressors → E[u|x]≠0 → OLS biased

• Example: Ability omitted in wage–education regression biases education effect

What is the Population Regression Function (PRF)?