Mechanics and Materials

vector

has magnitude and direction

scalar

has magnitude

moment

force x perpendicular distance from line of action of force

sum of clockwise moments _______ sum of anticlockwise moments

=

centre of mass

point at through which a single force on the body has no turning effect

couple

pair of equal and opposite forces 

moment of a couple

force x distance between couple 

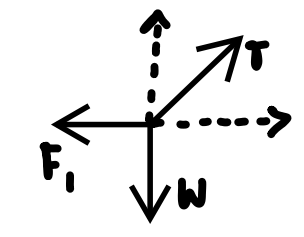
Resolve forces here

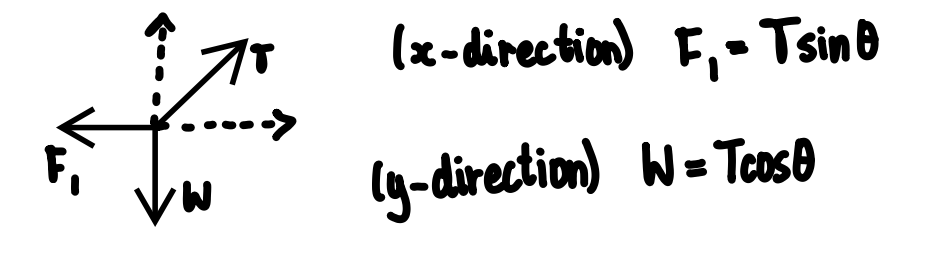
Resolve forces here

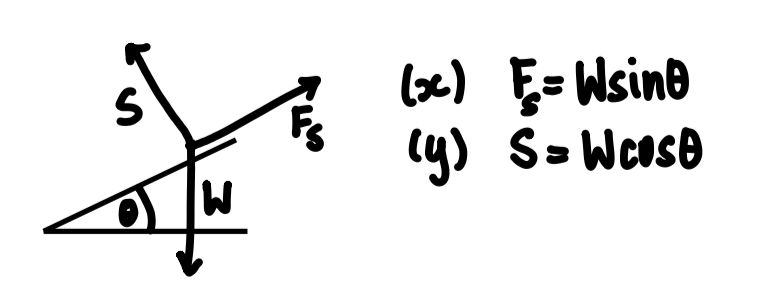
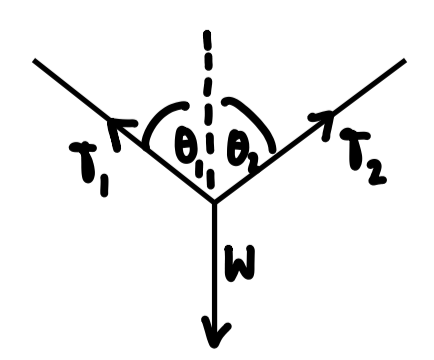
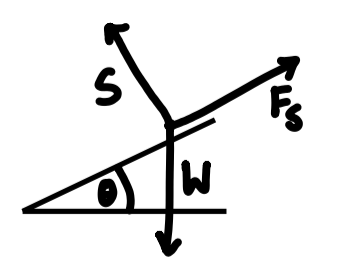
Resolve forces

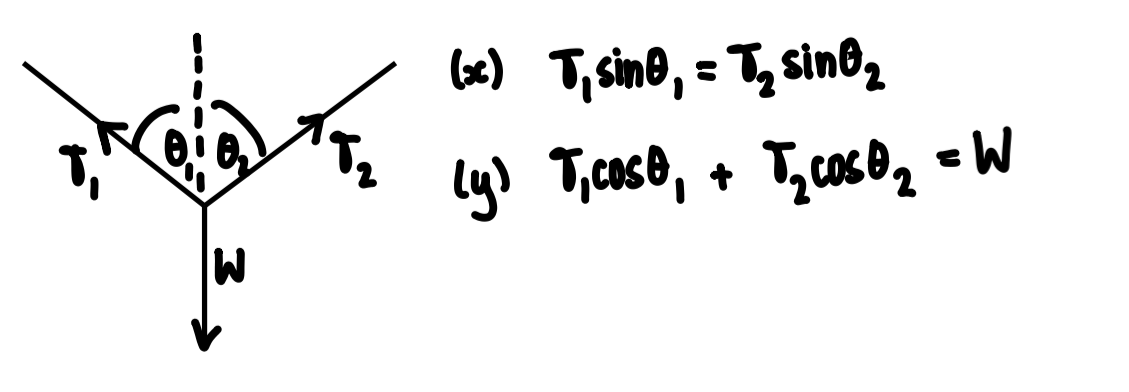
If the centre of mass is higher

a weight will topple over at a smaller angle 

Newton 1

Objects either stay at rest or move with constant velocity unless acted on by a force

Newton 2

F= ma

Stopping distance

Thinking distance + braking distance

Impact time 

2s/ u + v

Acceleration

v-u/t

F_R

ma

Force in term of energy and time

F= change in kinetic energy or work done/ time

momentum

mass x velocity 

Newton 2 in terms of momentum

rate of change of momentum is proportional to resultant force

Area under force-time graph

change in momentum

Newton 3

When two objects interact, they exert equal and opposite forces on eachother

Principle of conservation of momentum

total momentum before collision= total momentum after collision

Elastic collision

kinetic energy conserved

momentum conserved

Inelastic collision

Kinetic energy not conserved

momentum conserved

Work done in terms of force

W= Fscosθ

Area under force-distance 

work done

Area under force-extension

work done/ energy stored in spring

Equation for GPE and KE of a pendulum

½mv²= mg∆h

Power

∆E/∆t= ∆W/∆t

Power in terms of force

P=Fv

Motive power

energy per second waster due to resistive forces + Gain of kinetic energy per second

Efficiency

output power/ input power= useful energy/ total energy

Density equation

m/V

Hooke’s Law

The force needed to stretch a spring is directly proportional to the extension of a spring from its natural length

Hooke’s equation

F= k∆L

Stiffer spring

bigger k

For springs at parallel, total k

k= k₁ + k₂

For springs in series, total k

1/k= 1/k₁ + 1/k₂

Elastic potential energy

½F∆L= ½k∆L²

Tensile stress

T/A

Tensile strain

∆L/L

Young modulus

TL/ A∆L

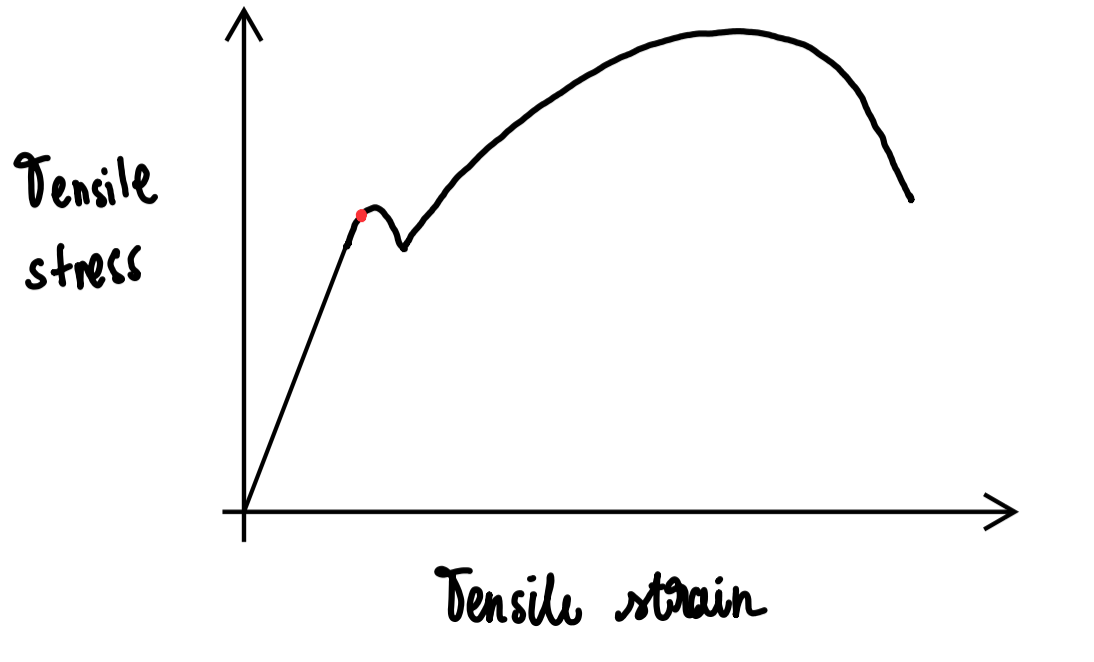
Elastic limit

plastic deformation

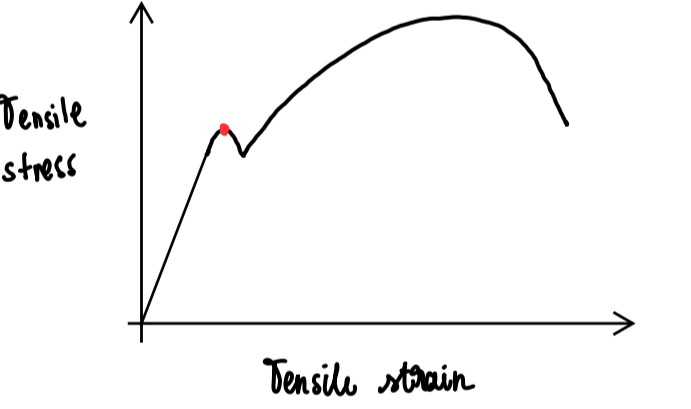
Yield point

wire temporarily weakens

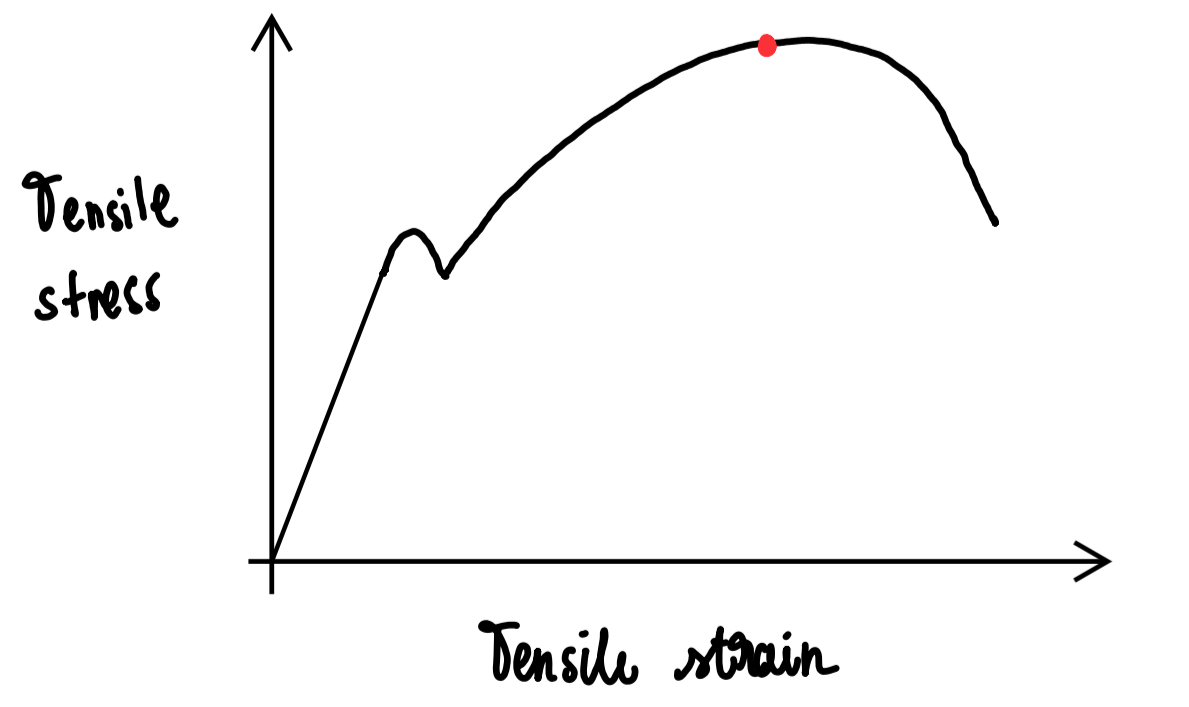
Ultimate tensile stress

strength

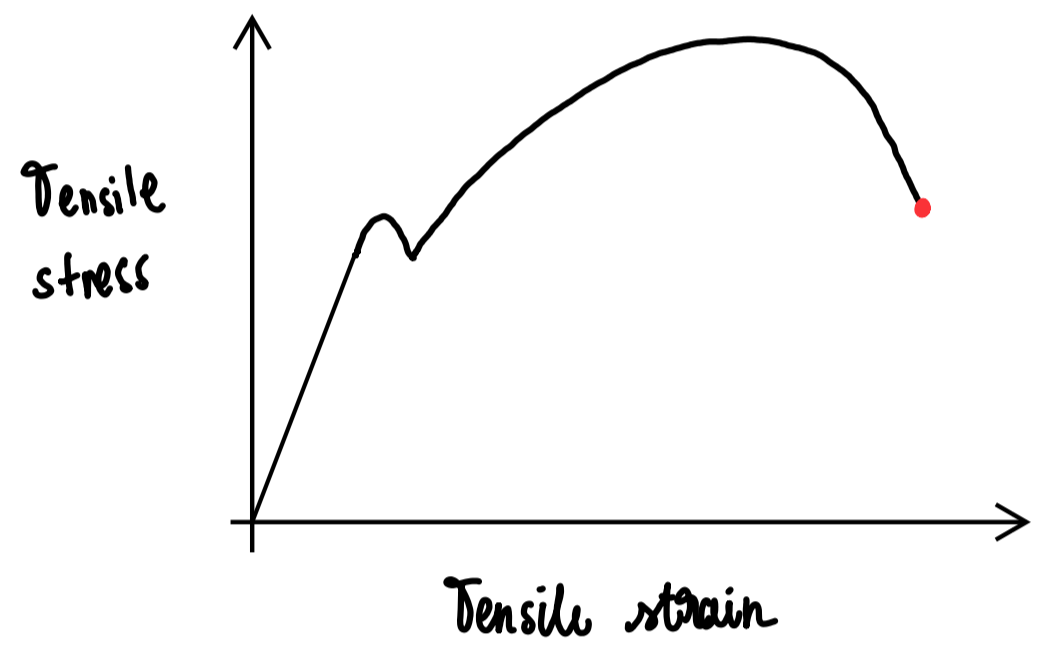
Breaking point

EPE in a stretched wire

½T∆L

Impulse

Ft