CCEA Maths M8 🔢

Pythagoras

𝑎² + 𝑏² = 𝑐²

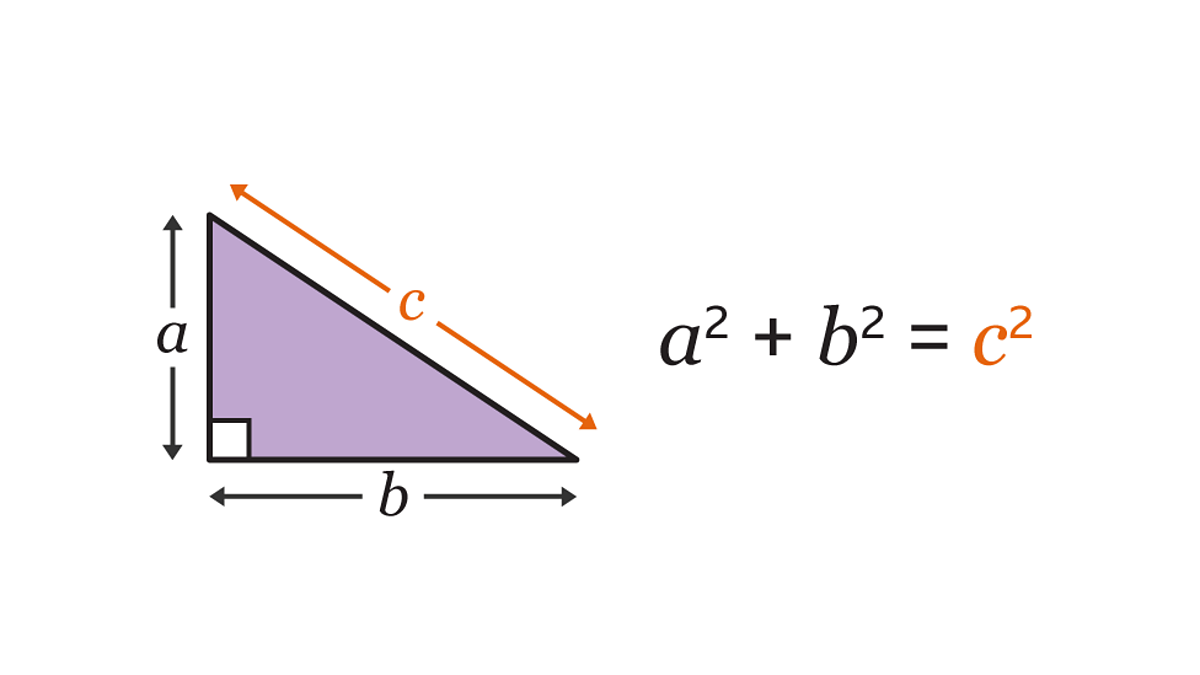
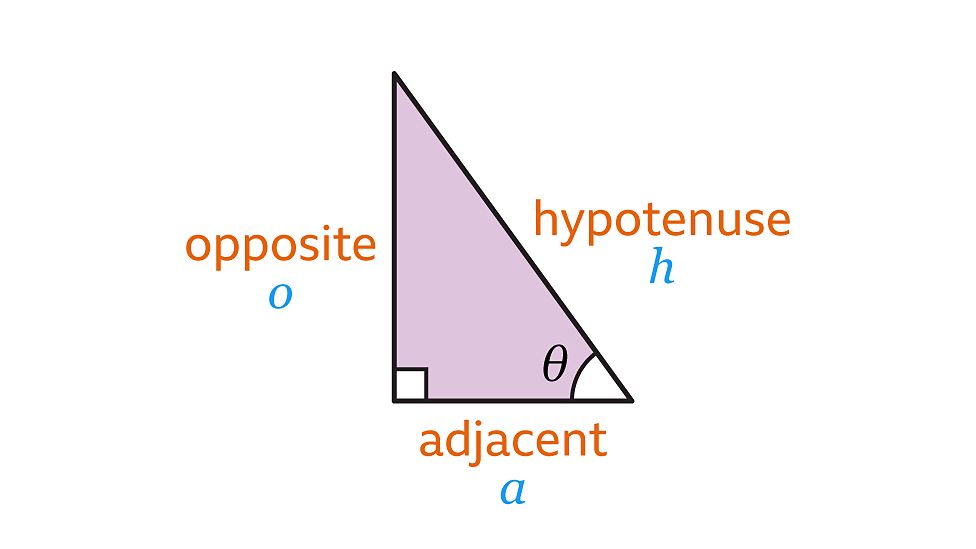
Trigonometry

• Sinθ = O/H

• Cosθ = A/H

• Tanθ = O/A

  use shift to find angle

Sine rule (formula given)

• 𝑎/sinA = 𝑏/sinB = 𝑐/sinC

• then cross multiply for angles, leave 𝑥 for sides

• question gives corresponding pair of angles and sides

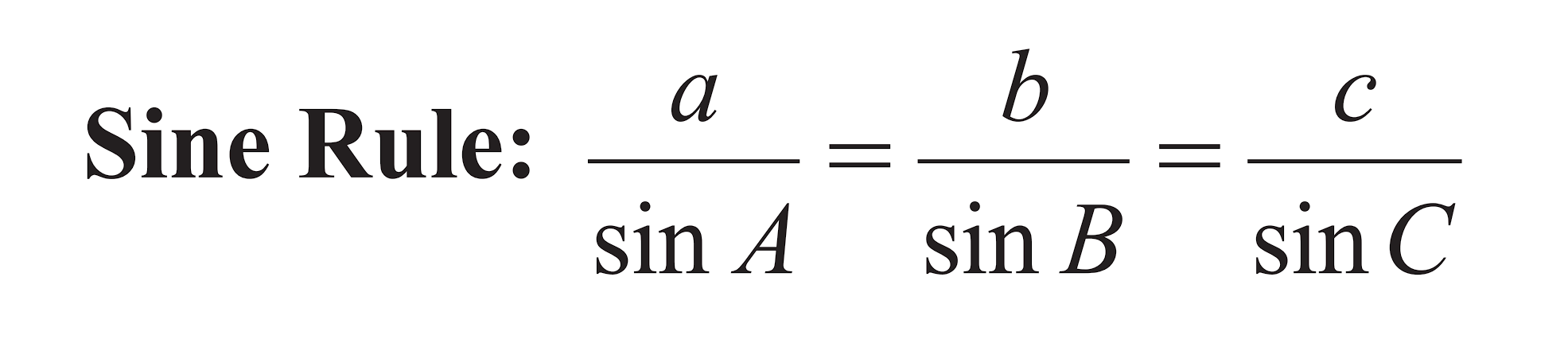
Cosine rule (formula given)

• 𝑎² = 𝑏² + 𝑐² - 2𝑏𝑐cosA

• question gives an angle and two sides that form it, asked to find other side

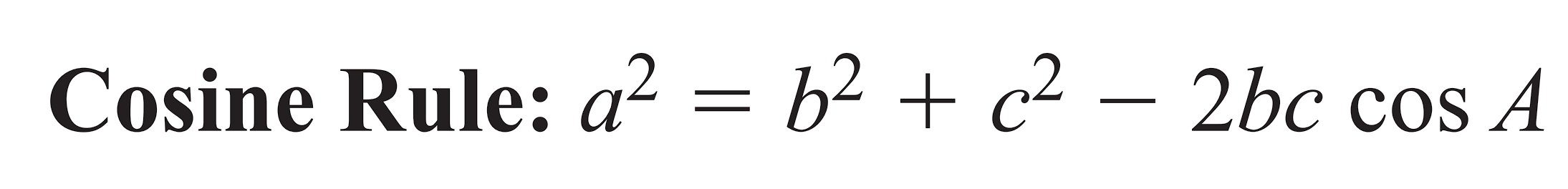
Rearranged cosine rule

• cosA = 𝑏² + 𝑐² - a²/ 2𝑏𝑐

  then use inverse cosine (cos^-1) to find A

• question gives all three sides and asked to find an angle

Area of triangle (formula given)

• area = 1/2𝑎𝑏sinC

• question gives an angle and two sides that make it

• make angle given or angle to find C

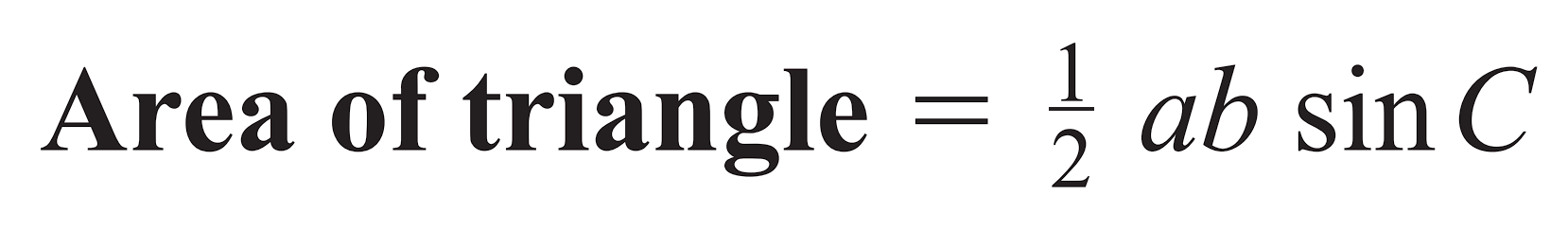
3D Trigonometry

• draw appropriate 2D shapes, join points and drop vertical

• apply either pythagoras or trig

Indices

𝑎^m × 𝑎ⁿ = 𝑎^m+n
𝑎^m ÷ 𝑎ⁿ = 𝑎^m-n
(𝑎^m)ⁿ = 𝑎^mn
𝑎⁰ = 1
𝑎^-m = 1/𝑎^m
𝑎^m/n = (_ⁿ√𝑎)^m

Angles of elevation/ depression

elevation is above horizontal, depression is below

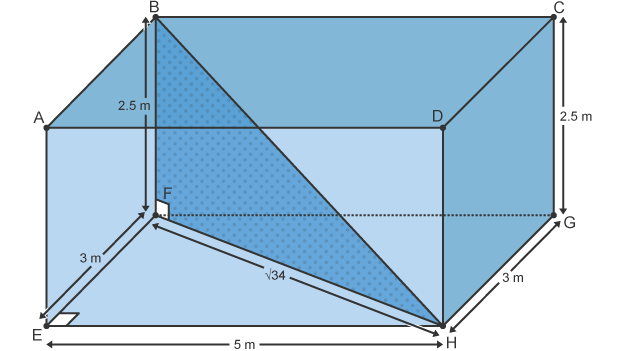
Standard form

• one digit before decimal point (1-10)

• count number of spaces moved

  • moving left is positive power, right is negative

• convert to decimal for calculations

Changing the subject

• identify the subject and use inverse operations

  • + → -

  • × → ÷

  • √𝑥 → 𝑥²

• may need to factorise if targets appears multiple times

• final answer must be subject = the rest

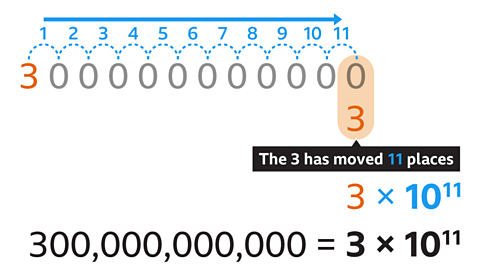
Circle equation (centre 0, 0)

• 𝑥² + 𝑦² = 𝑟²

• divide/ multiply equation if necessary to have 1 in front of x and y

• may need to sub in values if given other equations

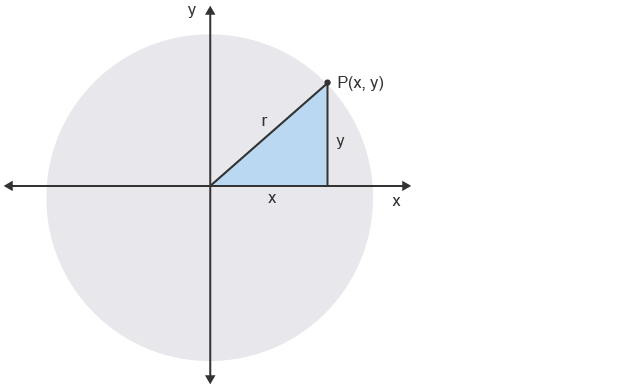
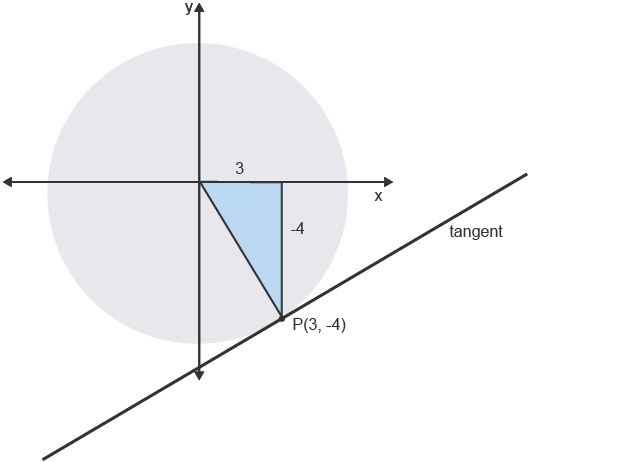
Tangent to circle

• perpendicular to radius so gradient is negative reciprocal

• sub in x and y at point tangent meets the circle

• crosses x-axis at (x, 0) and y-axis at (0, x)

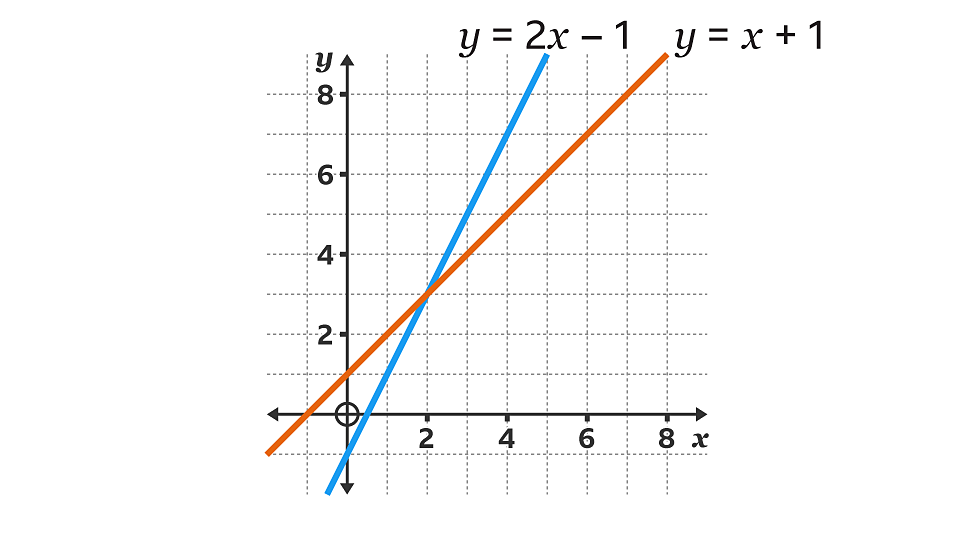
Linear simultaneous equations graphically

draw both equations, solution is where lines cross
e.g cross at (2, 3)
x = 2, y = 3

Linear simultaneous equations by substitution

𝑥𝑦 = 12
𝑦 - 3𝑥 + 9 = 0
*rearrange an equation into the form 𝑦 = *
𝑦 = 3𝑥 - 9
*substitute for y in first equation*
𝑥(3𝑥 - 9) = 12
*calculate values of remaining letter*
3𝑥² - 9𝑥 - 12 = 0 (quadratic)
(𝑥 - 4)(𝑥 + 1) = 0
𝑥 = 4 𝑥 = -1
*substitute into equation to find values of other letter*
𝑥𝑦 = 12
𝑥 = 4 𝑦 = -3
𝑥 = -1 𝑦 = -12

Linear simultaneous equations by elimination

3𝑥 + 𝑦 = 11
𝑥 + 𝑦 = 5
*eliminate one letter from both equations, divide/ multiply if necessary*
3𝑥 + 𝑦 = 11
𝑥 + 𝑦 = 5
*same signs subtract, different signs add*
2𝑥 = 6
𝑥 = 3
*substitute into equations to find value of other letter*
𝑥 + 𝑦 = 5
3 + 𝑦 = 5
𝑦 = 2

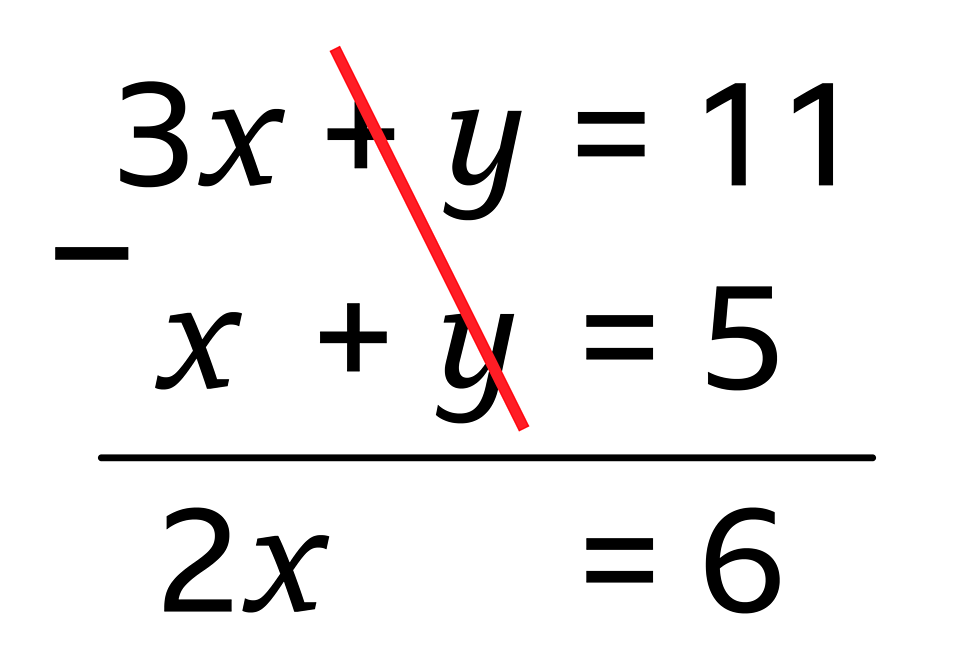
Quadratic simultaneous equations

• substitute linear equation into quadratic

• solve using factorisation or quadratic formula

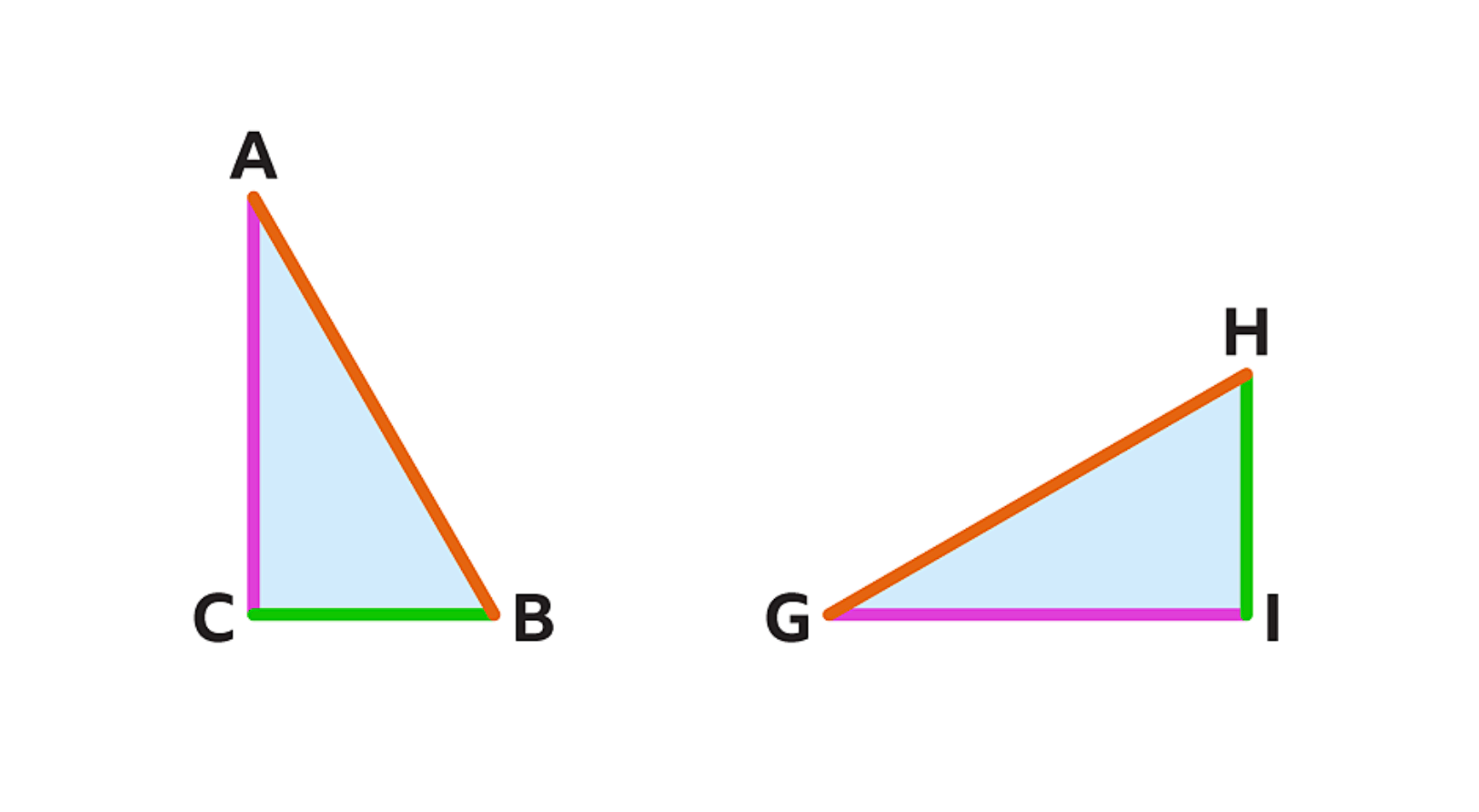
Congruent

• shapes that are identical in shape and size, may be reflected or rotated

  • they have equal lengths and angles

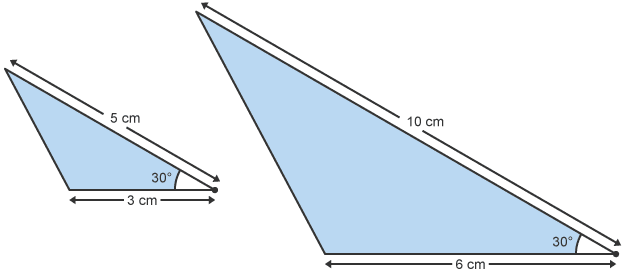
Similar

• shapes that are proportional in shape and size, may be reflected or rotated

  • lengths are enlarged by scale factor

  • they have equal angles

Effect of scale factor

• ratio of similar shapes

  • length of sides/ perimeter is equal to scale factor e.g 2

  • area is equal to scale factor squared e.g 2² = 4

  • volume is equal to scale factor cubed e.g 2³ = 8

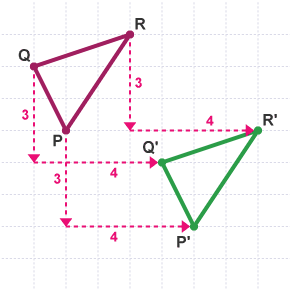
Translation

• every point in shape is translated (move) up/down/left/right

• count distance moved between points e.g 4 right, 3 down

• column vectors are used to describe it e.g (⁴_-3)

  • (^𝑎_𝑏) 𝑎 shows horizontal, 𝑏 shows vertical

  • +ve to show right/up

  • -ve to show left/down

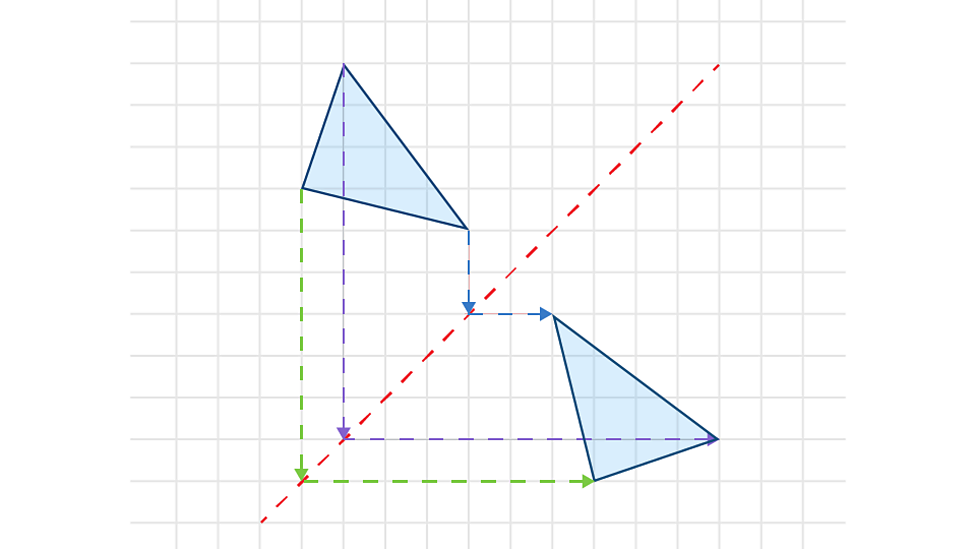
Reflection

• every point in shape is reflected (flipped) in line e.g y = x

  • line can be vertical, horizontal or diagonal

• count distance from line of reflection and plot on other side

  • 𝑦 = 𝑎 (𑁋) 𝑥 = 𝑎 ( ⏐ )

  • 𝑦 = 𝑥 (╱) 𝑦 = -𝑥 (╲)

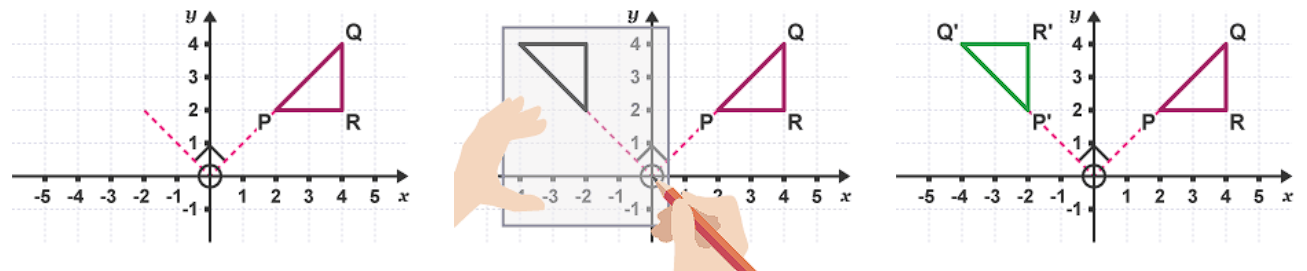
Rotation

• every point in shape is rotated (turned) about fixed point, the centre of rotation

• determine degrees rotated, clockwise or anticlockwise

• use tracing paper to draw rotation

  • trace around shape on paper

  • hold down pencil at the centre of rotation

  • rotate tracing paper and copy the image

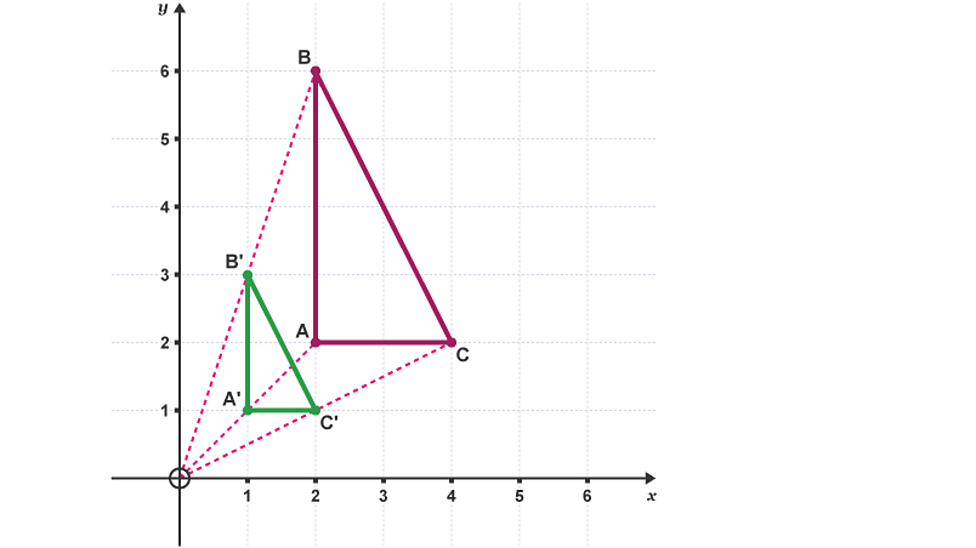
Enlargement

• every point in shape is enlarged (grown) by scale factor about fixed point, the centre of enlargement

• multiply distance from centre to original shape by scale factor

  • fractional scale factor makes it smaller

  • -ve scale factor makes it bigger in the opposite direction

• draw lines through corners of shapes, they meet at centre of enlargement

Linear sequences

𝑛^th term = 𝑎𝑛 + 𝑏

• find common difference

• multiply by 𝑛

• add number before first term

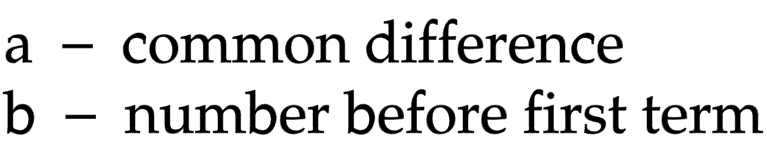
Fraction sequences

treat as two linear sequences and give answer as fraction e.g 𝑛/ 2𝑛 + 1

• top is 𝑛^th term of numerator sequence

• bottom is 𝑛^th term of denominator sequence

Quadratic sequences

𝑛^th term = 𝑎𝑛² + 𝑏𝑛 + 𝑐

• find difference and half it

• write out sequence of 𝑎𝑛²

• subtract from original sequence to give linear

• find 𝑛^th as normal

Probability

• written as decimal or fraction, all probabilities add up to 1

• P = number of outcome/ total possible outcomes

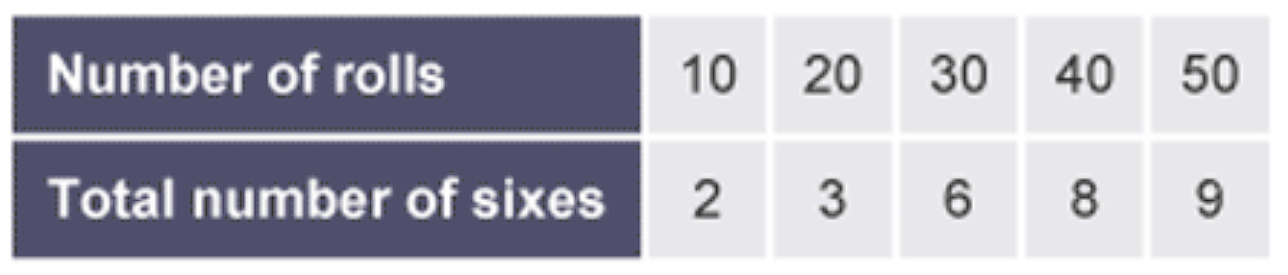
Relative frequency

• higher number of trials is more reliable

• RF = number of times event happens/ total number of trials

• expected number = probability × total number of trials

Product rule for counting

• to find total number of outcomes multiply number of outcomes for each event

• e.g menu offers 4 starters, 7 mains and 3 desserts

  • ∴ 4 × 7 × 3 = 84 combinations

Mutually exclusive (OR → ADD)

• two events that can’t happen at the same time

• P(A or B) = P(A) + P(B)

Independent events (AND → MULTIPLY)

• outcome of first event does not affect outcome of another event

• P(A and B) = P(A) × P(B)

Dependent events (THEN → MULTIPLY CONDITIONAL)

• outcome of first event does affect outcome of another event

• P(A then B) = P(A) × P(B;A)

  • ;A js means A already happened, not replaced

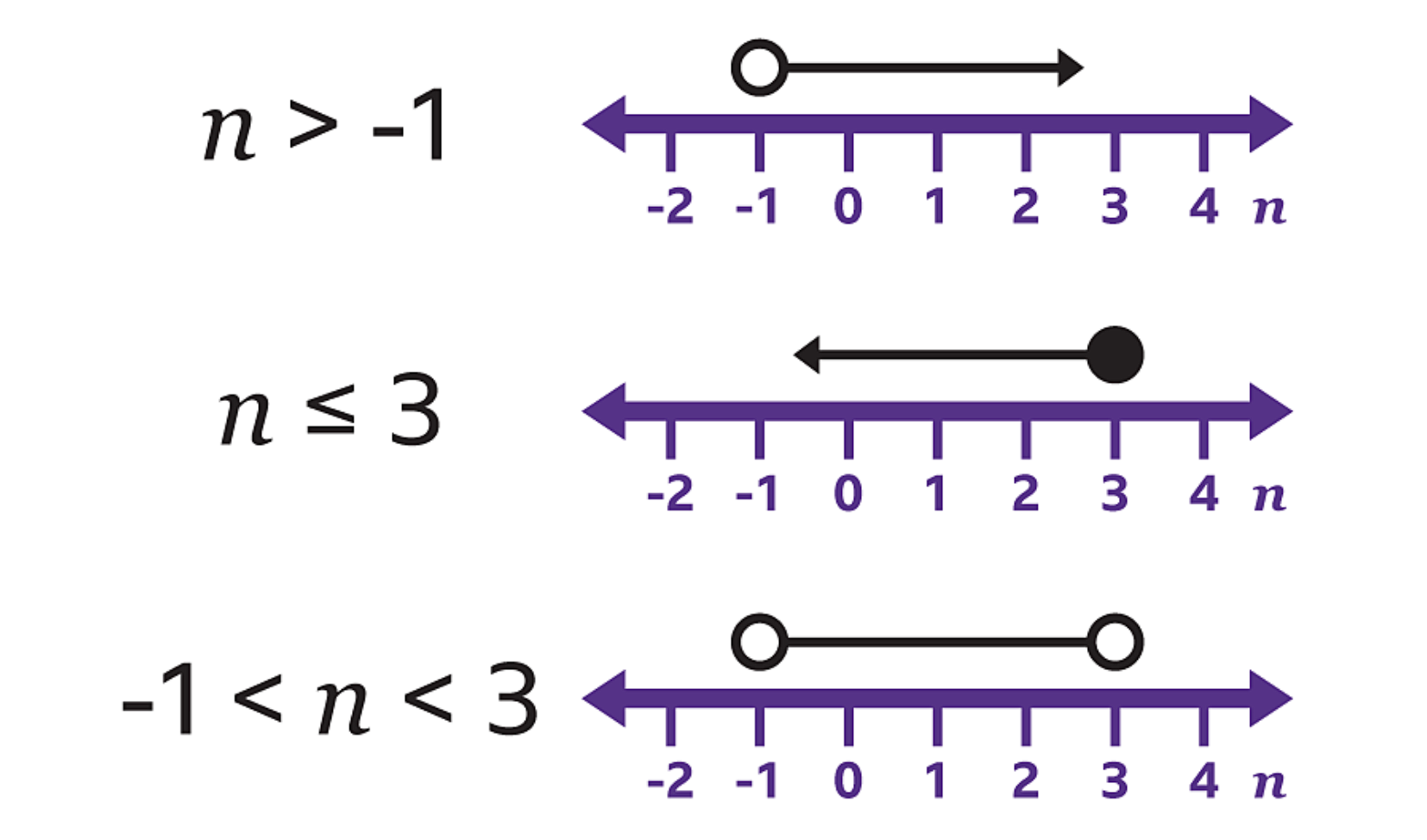
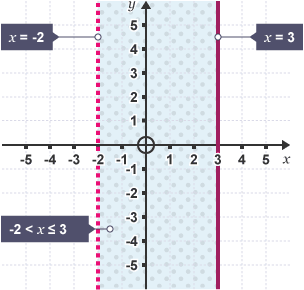
Inequalities on number line

• use ‘x’ for integer values and arrows for real values

  • ●→ including (≤ or ≥)

  • ○→ not including (< or >)

Inequalities graphically

• < or > dashed line (┈)

• ≤ or ≥ solid line (━)

• when shading, sub in a point to inequality, if it is correct keep that side, if not shade it

Solving inequalities

• same as equations but replace = in solution with inequality sign

• split double inequalities and solve separately

Rational

can be written as a fraction, includes recurring decimals

Irrational

can’t be written as a fraction e.g multiples of π or √ of non square

Fraction to decimal

divide numerator by denominator until you get repeated pattern

Decimals to fraction

put decimal over 1 and multiply by 10, 100 or 1000, then simplify

Recurring decimals to fractions

0.816
*let 𝑟 equal recurring decimal*
𝑟 = 0.816816816816
*multiply by 10, 100 or 1000, maintaining pattern after decimal*
1000𝑟 = 816.816816816816
*take 𝑟, or a multiple of 𝑟, away so recurring decimal cancels out*
1000𝑟 - 𝑟 = 999𝑟
999𝑟 = 816.816816 - 0.816816
999𝑟 = 816
*place in fraction and simplify*
𝑟 = 816/999
𝑟 = 272/333

If asked for exact value

leave as surd or fraction of recurring decimal

Surds

√𝑎 × √𝑎 = (√𝑎)² = 𝑎

√𝑎 × √𝑏 = √𝑎 × 𝑏
√𝑎 ÷ √𝑏 = √𝑎 ÷ 𝑏

𝑐√𝑏 × 𝑑√b = 𝑐 × 𝑑√𝑏
𝑐√𝑏 ÷ 𝑑√b = 𝑐 ÷ 𝑑√𝑏

𝑎√𝑏 ± 𝑐√b = 𝑎 ± 𝑐√𝑏

√𝑎 = 𝑎^1/2

FOIL

(2 + √5)(2 - √5)
*multiply First, Outside, Inside and Last*
𝑥² - 2√5 + 2√5 - 5

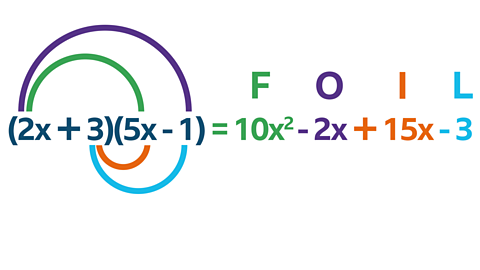
Simplifying surds

√75 + 9√12
*rewrite surds as product of 2 numbers, one the largest square factor*
√(25 × 3) + 9√(4 × 3)
*square root factor*
√(5² × 3) + 9√(2² × 3)
*square root takes outside surd*
5√3 + 9 × 2√3
*combine surds*
5√3 + 18√3 = 23√3

Rationalising the denominator

6 + √3 / √3
*multiply numerator and denominator by surd, √3*
6 + √3 × √3 / √3 × √3
*simplify surds*
6 + √3 / 3
*simplify fraction*
2 + √3

Binary

• number system based on powers of 2

• place value: 64 32 16 8 4 2 1

• numbers are either 1 or 0

Binary to decimal

100111
*put in place values*
64 32 16 8 4 2 1
0 1 0 0 1 1 1
*sum place values multiplied by numbers*
64(0) + 32(1) + 16(0) + 8(0) + 4(1) + 2(1) + 1(1)
= 39

Decimal to binary

84
*divide by 2 until 0, include remainder*
84 ÷ 2 = 42 r 0
42 ÷ 2 = 21 r 0
21 ÷ 2 = 10 r 1
10 ÷ 2 = 5 r 0
5 ÷ 2 = 2 r 1
2 ÷ 2 = 1 r 0
1 ÷ 2 = 0 r 1
*read remainders going upwards*
1010100

Compound interest

𝑝(1 + 𝑟 ÷ 100)^𝘵

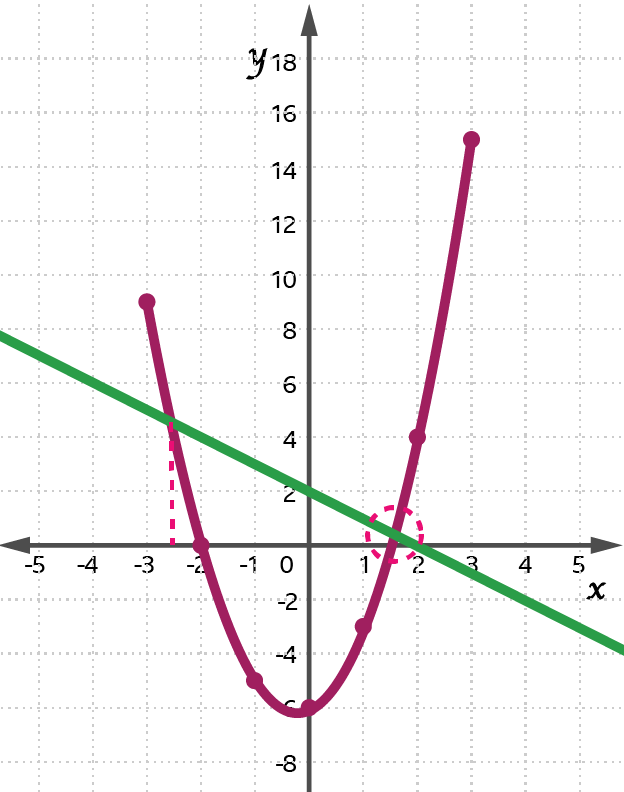
Graphical Solutions

• find difference of equations; equation of graph drawn subtract equation given

  • 2𝑥² + 𝑥 - 6 = 0 is drawn

  • 2𝑥² + 2𝑥 - 8 = 0 is given

  • -𝑥 + 2 is the difference

• draw linear graph of the difference

• x value at points of intersection on graph are solution

Quadratic graph

𝑦 = 𝑎𝑥² + 𝑏𝑥 + 𝑐𝑏

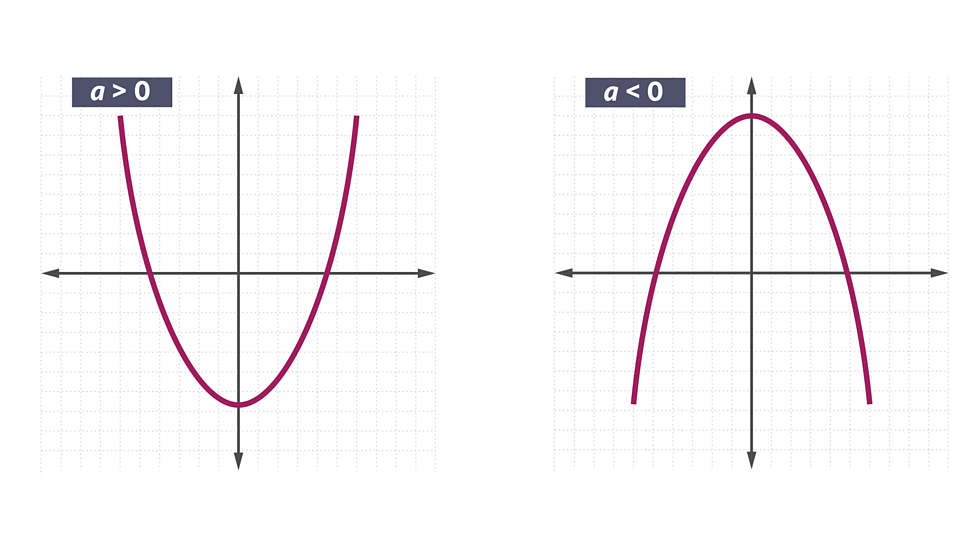
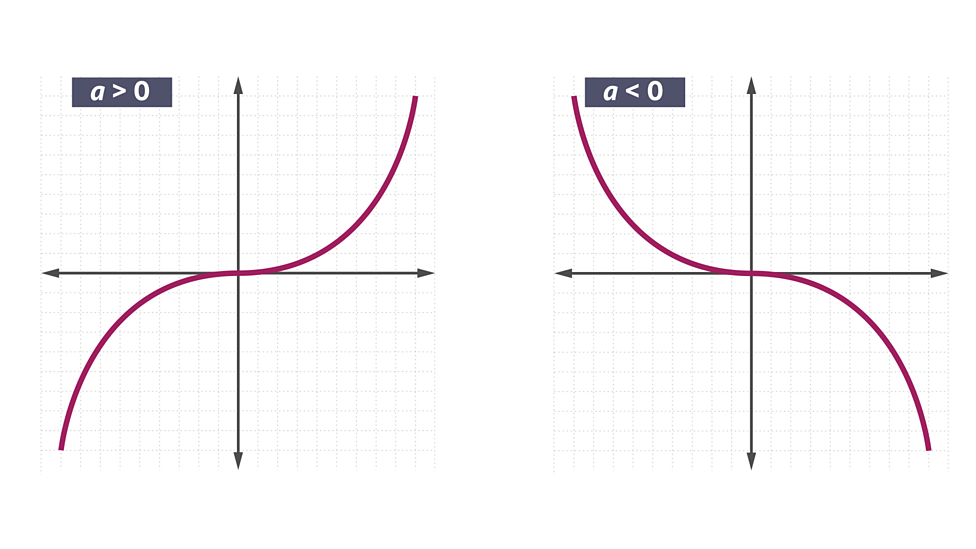
Cubic graphs

𝑦 = 𝑎𝑥³ + 𝑏𝑥² + 𝑐𝑏 + 𝑑

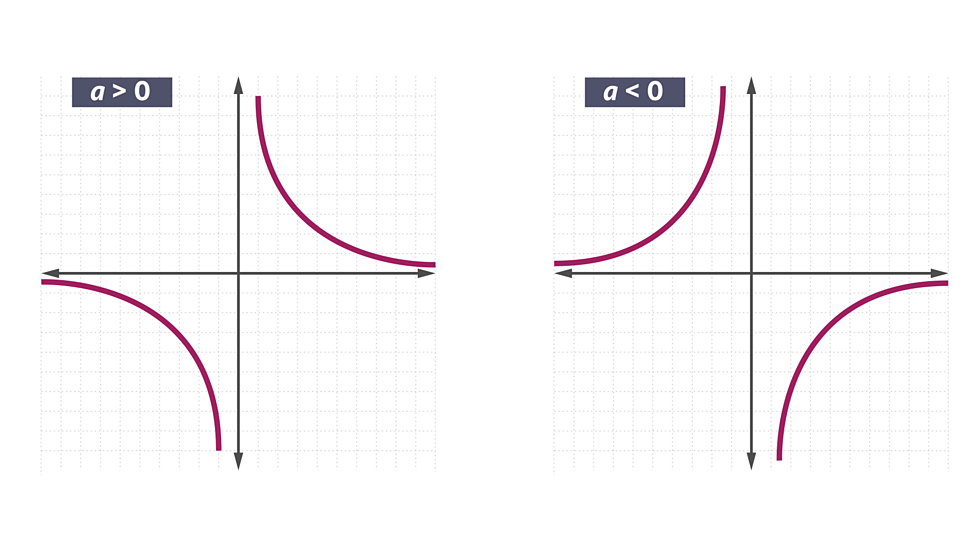
Reciprocal graphs

𝑦 = 𝑎/𝑥

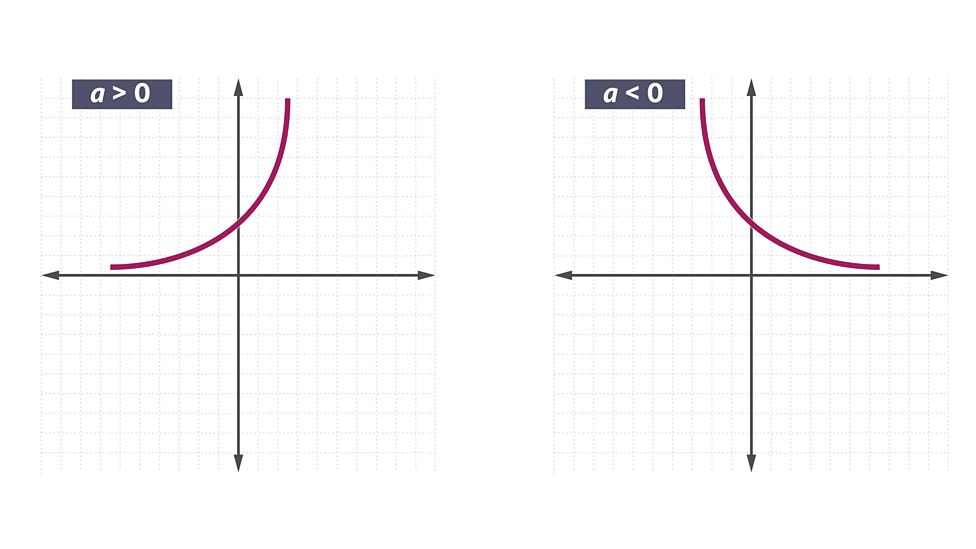
Exponential graphs

𝑦 = 𝑎^𝑥

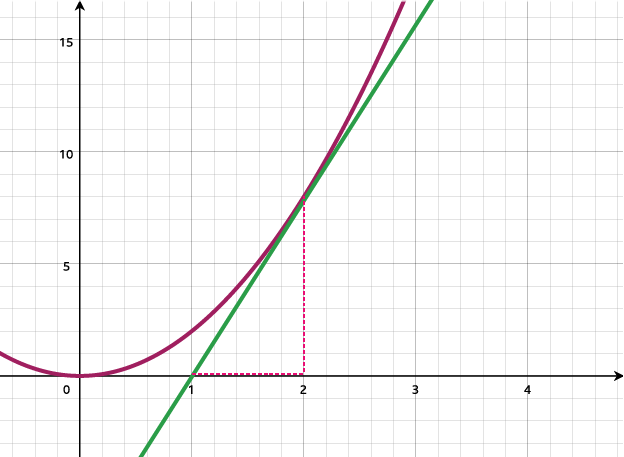
Gradient of a curve

• draw tangent at the point on the curve

• use gradient equation (rate of change at that point)

  e.g gradient of curve when x = 2 is 8

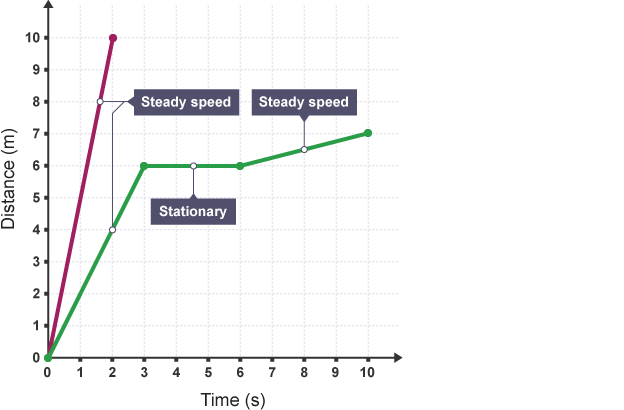
Speed

• speed = distance ÷ time

• always check units

• when reading graph

  • steeper line means travelling faster

  • horizontal line means its stopped

  • if velocity, line going down means travelling back

Bearings

• measured from north

• given in 3 figures

Angles in polygons

• sum of exterior = 360°

• sum of interior = (𝑛 - 2) × 180

• interior + exterior = 180°

• exterior of regular polygon = 360/ 𝑛

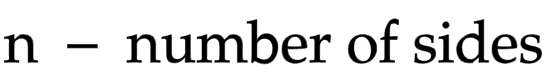
Direct proportion

𝑇 ∝ 𝑟 → 𝑇 = 𝑘𝑟

Indirect proportion

𝑇 ∝ 1/𝑟 → 𝑇 = 𝑘/𝑟

Gradient

(𝑦₂ - 𝑦₁) ÷ (𝑥₂ - 𝑥₁)

Length of line

√(𝑥₂ - 𝑥₁)² + (𝑦₂ - 𝑦₁)²

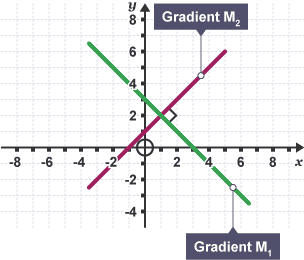
Parallel lines

same gradient

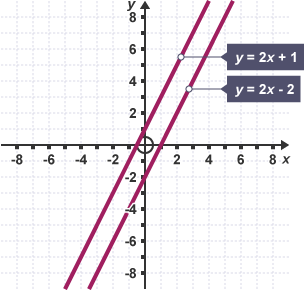
Perpindicular lines

negative reciprocal gradient (flip fraction + change sign)

Constructions and loci

show all construction arcs to get marks

Metric and imperial unit conversion

• 1 inch ≈ 2.5cm

• 1 mile ≈ 1.6km

• 1kg ≈ 2.2 lbs

• 1 litre ≈ 1.75 pints

Square numbers

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225

Cube numbers

1, 8, 27, 64, 125, 216

Prime numbers

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31