Bivariate Linear Regression (Week 9)

Purpose of Bivariate Linear Regression

To predict one variable from another variable using a straight line.

Bivariate Linear Regression Analysis

If two variables are correlated, you can use one to predict the other.

What does bivariate linear regression estimate?

Estimates parameters in a linear equation that can be used to predict values of one variable based on the other.

Equation for bivariate linear regression

Y = a + bX

Key advantage of bivariate linear regression

Provides a more detailed analysis, which includes an equation that can be used for prediction and/or optimization

IV and DV in bivariate linear regression

X must be the IV (aka the predictor)

Y must be the DV (aka the outcome)

To say that X is a predictor of Y, you must be able to establish:

• Temporal Precedence (cause happens before effect) 

• Causal Mechanism (how exactly X affects Y/ the why) 

• Not better accounted for by correlation (JUST correlation) 

• No third variable causation ( spurious effects, confounding variables) 

  • If you cannot do all the above, it is association (correlation) 

Linear regression fits a ___ line to the data that is added to the scatterplot. This fitted line helps to ___ whether or not a ___ regression is a good fit to the data. 

1. straight 

2. show 

3. linear

The two components to describe bivariate linear regression dataset

1. Trend (the general linear tendency)

   1. positive or negative direction of the relationship

2. Scatter (variation from the trend) 

How does bivariate linear regression work?

• If a linear regression model is appropriate, then the fitted line (regression line) is used to predict a value of the response (dependent) variable for a given value of the explanatory (independent) variable 

• Also describes change y/ change x, AKA slope 

• Estimates the true, but unknown, linear relationship between the two variables

How is slope calculated?

Rise over run

OR

change in y divided by change in x

Equation for general regression line

Y’ = bX + a

Y’: Predicted Y score 

b = Slope 

X = Score for the predictor 

a = Y-intercept ( value for where the regression line crosses the vertical axis, CONSTANT) 

Standard error of estimate ( s_e)

• The regression line will never perfectly pass through every data point

• These errors are also called “residuals” individually

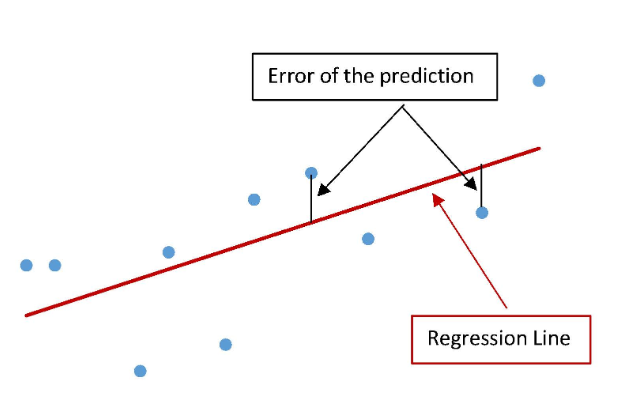
What does the standard error of estimate indicate?

• Indicates, on average, how much the actual Y values differ from those predicted by the regression line Y’

• Higher r = higher r² = better the predication = lower

If our predication errors are normally distributed, s_e can be used to make a ___ ___ for our predictions 

confidence interval 

Y’ ± 1 Standard Error of Estimate = The range of predicted Y’ scores that will contain the actual Y ___% of the time 

68%

Y’ ± 2 Standard Error of Estimate = The range of predicted Y’ scores that will contain the actual Y ___% of the time 

95%

Y’ ± 3 Standard Error of Estimate = The range of predicted Y’ scores that will contain the actual Y ___% of the time 

99%

Assumptions of Bivariate Linear Regression

1. Linearity: The two variables have a linear relationship

2. Normality: The two variables are approximately normally distributed

3. Independence: The measurements from each participant are in no way related to measurements from other participants 

4. Homoscedasticity: The prediction of Y values is just as good/bad for all X values 

How to check assumptions of Bivariate Linear Regression

1. Linearity: check the scatterplot

2. Independence: study design 

3. Normality: not needed for this class 

4. Homoscedasticity: not needed for this class